
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определения и основные понятия
Напомним, что 1). сеть – это связный ориентированный граф без петель и циклов; 2) вход  – вершина сети, у которой
– вершина сети, у которой 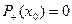 , а выход – вершина сети
, а выход – вершина сети  , у которой
, у которой 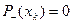 ; 3) каждая дуга сети ориентирована от входа к выходу, то есть лежит на некотором пути от входа к выходу.
; 3) каждая дуга сети ориентирована от входа к выходу, то есть лежит на некотором пути от входа к выходу.
Определение 1. Вершину сети, не являющуюся входом или выходом будем называть промежуточной.
Определение 2. Пропускная способность – это неотрицательная функция (нагрузка) 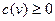 , заданная на множестве
, заданная на множестве 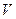 дуг сети
дуг сети 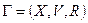 .
.
Пусть 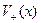 - множество дуг, входящих в вершину
- множество дуг, входящих в вершину 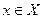 и
и 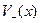 - множество дуг, выходящих из вершины
- множество дуг, выходящих из вершины 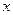 . Далее без ограничения общности будем считать, что сеть имеет единственный вход
. Далее без ограничения общности будем считать, что сеть имеет единственный вход  и единственный выход
и единственный выход  .
.
Определение 3. Потоком называется такая числовая функция 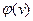 , что:
, что:
1). 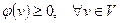 ; 2).
; 2). 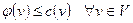 ;
;
3). 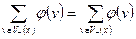 для любой промежуточной вершины
для любой промежуточной вершины 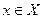 .
.
Последнее условие называется условием неразрывности потока  . Оно означает, что «сколько втекает в промежуточную вершину, столько из нее и вытекает».
. Оно означает, что «сколько втекает в промежуточную вершину, столько из нее и вытекает».
Определение 4. Величина 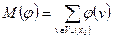 называется мощностью потока.
называется мощностью потока.
Определение 5. Поток максимальной мощности называется максимальным.
Обозначим 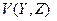 множество дуг с началом в
множество дуг с началом в  и концом в
и концом в 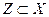 .
.
Определение 6. Пусть 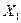 ,
,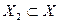 и
и 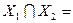 Ø. Назовем потоком из
Ø. Назовем потоком из 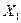 в
в 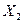 величину
величину 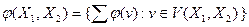 . В случае
. В случае 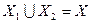 величину
величину 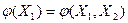 назовем потоком из
назовем потоком из 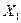 .
.
Таким образом, 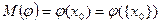 - поток из входа
- поток из входа  .
.
Замечание 1. Условие неразрывности имеет вид: 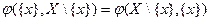 для любой промежуточной вершины
для любой промежуточной вершины 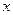 .
.
Определение 7. Разрезом 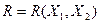 сети
сети 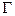 называется разбиение множества вершин
называется разбиение множества вершин 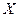 сети
сети 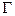 на два таких подмножества
на два таких подмножества 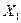 и
и 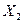 , что:
, что:
1) 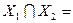 Ø,
Ø,
2) 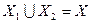 ,
,
3) вход 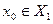 , а выход
, а выход 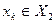 .
.
Множество 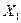 называется входным, а
называется входным, а 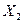 – выходным. Далее
– выходным. Далее
Определение 8. Дуга 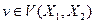 называется разрезанной разрезом
называется разрезанной разрезом 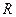 .
.
Множество всех разрезанных дуг обозначается 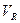 .
.
Определение 9. Величину 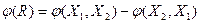 назовем потоком через разрез
назовем потоком через разрез 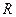 .
.
Замечание 2. Если 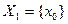 ,
,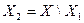 и
и 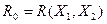 , то
, то 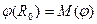 .
.
Определение 10. Пропускной способностью разреза 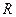 называется сумма пропускных способностей дуг этого разреза:
называется сумма пропускных способностей дуг этого разреза: 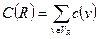
Определение 11. Разрез минимальной пропускной способности называется минимальным.
Определение 12. Дуга называется насыщенной, если 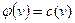 .
.
Очевидно, что для ненасыщенной дуги 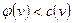 .
.
Теорема 1. Для любого разреза 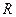 справедливо равенство
справедливо равенство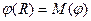 .
.
Доказательство проведем индукцией по мощности 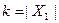 входного множества. При
входного множества. При 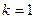 имеем, что
имеем, что 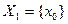 и
и 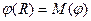 в силу замечания 1.
в силу замечания 1.
Пусть утверждение справедливо для всех  и входное множество
и входное множество 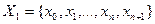 разреза
разреза 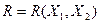 имеетмощность
имеетмощность 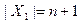 (соответствующее выходное множествоимеет вид
(соответствующее выходное множествоимеет вид 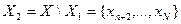 ). Рассмотрим разрез
). Рассмотрим разрез 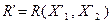 , где
, где 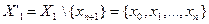 (следовательно,
(следовательно, 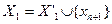 ) и
) и 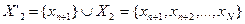 . Тогда
. Тогда 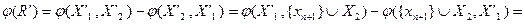
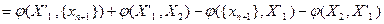 . С другой стороны,
. С другой стороны,
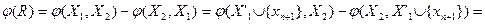
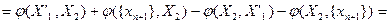
Отсюда следует, что 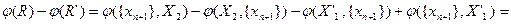
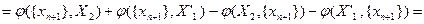
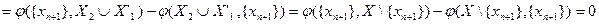
Здесь последнее равенство справедливо в силу замечания 1. Поскольку 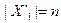 , то по предположению индукции
, то по предположению индукции 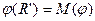 , и, следовательно,
, и, следовательно, 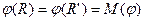 . Теорема доказана.
. Теорема доказана.
Теорема 2. Мощность 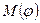 любого потока
любого потока  не превосходит пропускной способности любого разреза
не превосходит пропускной способности любого разреза 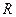 :
: 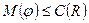 .
.
Доказательство. Поскольку 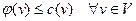 , то в силу теоремы 1
, то в силу теоремы 1 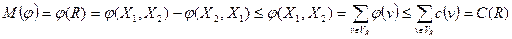 .
.
Теорема доказана.
Следствие. Если для потока  и разреза
и разреза 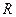 справедливо равенство
справедливо равенство 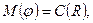 то
то  – максимальный поток, а
– максимальный поток, а 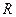 – минимальный разрез.
– минимальный разрез.
Доказательство очевидно.
Замечание 2. Если 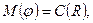 то все дуги разреза
то все дуги разреза 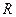 - насыщенные и
- насыщенные и  . Действительно, если дуга
. Действительно, если дуга 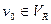 ненасыщенная, то
ненасыщенная, то 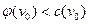 , и, следовательно,
, и, следовательно, 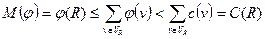 . Если же
. Если же 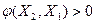 , то
, то
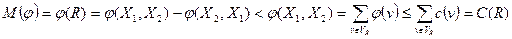 .
.
|
Дата добавления: 2014-01-20; Просмотров: 437; Нарушение авторских прав?; Мы поможем в написании вашей работы!