
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример решения задачи о максимальном потоке
|
|
|
|
Рассмотрим пример решения задачи о максимальном потоке.
Пусть дана сеть с определенной на ней пропускной способностью (на рисунке 1 и далее мы для простоты опускаем индексы, указывая, например, на дуге  пропускную способность в виде
пропускную способность в виде 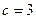 вместо более точной записи
вместо более точной записи  .)
.)


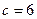







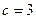

Рис. 1. 
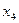
1. Определим начальный поток 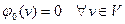 . Разумеется,
. Разумеется,  .
.
 |

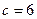















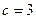


Рис. 2. 
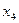
2. Алгоритм Форда-Фалкерсона построения максимального потока в сети.
Определение 13. Цепь 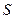 от входа
от входа  до выхода
до выхода  называется повышающей поток
называется повышающей поток  , если выполнены условия 1.
, если выполнены условия 1.  и 2.
и 2.  .
.
Будем искать повышающую цепь 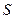 , начиная от входа
, начиная от входа  с помощью алгоритма пометок, который излагается ниже.
с помощью алгоритма пометок, который излагается ниже.
В соответствии с определением 13 сформулируем простое правило: пометки можно наносить либо по ненасыщенным дугам по направлению дуги или по дугам, на которых  , но в обратном направлении (по “обратным” дугам). Повторно пометки не наносятся.
, но в обратном направлении (по “обратным” дугам). Повторно пометки не наносятся.
Вначале пометим звездочкой вход сети  . Из
. Из  по исходящим дугам пометим вершины
по исходящим дугам пометим вершины  и
и  . В качестве пометки будем использовать обозначение самой вершины
. В качестве пометки будем использовать обозначение самой вершины  , указывая его в скобках рядом с помеченной вершиной.
, указывая его в скобках рядом с помеченной вершиной. 
 (
( )
) 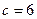









 *
* 




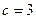


Рис. 3.  (
( )
) 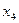
Теперь просматриваем помеченные вершины  и
и  в каком-либо фиксированном порядке, например, сверху вниз. Вначале просмотрим вершину
в каком-либо фиксированном порядке, например, сверху вниз. Вначале просмотрим вершину  . Из нее п
. Из нее п ометим вершины
ометим вершины  и
и 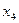 (вершина
(вершина  уже помечена).
уже помечена).
( )
) 
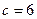

 (
( )
)







 *
* 





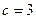

Рис. 4.  (
( )
) 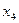 (
( )
)
Из вершины  ничего не помечаем, поскольку вершина
ничего не помечаем, поскольку вершина  уже помечена.
уже помечена.
Пр осмотрим вершины
осмотрим вершины  и
и 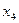 . Из
. Из  пометим вершину
пометим вершину  - выход сети.
- выход сети.
 (
( )
) 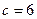

 (
( )
)







 *
*  (
( )
)




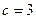


Рис. 5.  (
( )
) 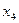 (
( )
)
На этом алгоритм пометок заканчивает свою работу. Выписываем построенную первую повышающую цепь  , начиная с вершины
, начиная с вершины  , помеченной, как это видно на рисунке 5, из вершины
, помеченной, как это видно на рисунке 5, из вершины  , помеченной из
, помеченной из  , в свою очередь помеченной из
, в свою очередь помеченной из  . Таким образом, имеем:
. Таким образом, имеем: 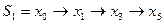 .
.
Пусть 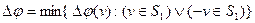 , где
, где  (1).
(1).
В силу условий 1. и 2. определения 13  и
и  , если
, если  , и
, и 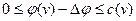 , если
, если  . Найдем новый поток
. Найдем новый поток  , полагая
, полагая
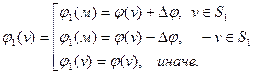 (2).
(2).
Так как в нашем случае дуги  ,
,  и
и  включены в цепь
включены в цепь  , то
, то 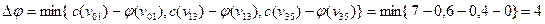 и
и  ,
,  ,
,  .
.
Ясно, что для так определенного нового потока  условие неразрывности (как и все остальные условия определения 3) будет выполнено. Новый поток
условие неразрывности (как и все остальные условия определения 3) будет выполнено. Новый поток  изобр
изобр азим на следующем рисунке. Ясно, что
азим на следующем рисунке. Ясно, что  .
.


















Рис. 6. 
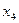
Как обычно, на рисунке индексы для простоты опускаем. Здесь для удобства мы отметили пунктиром насыщенную дугу  , поскольку на следующем шаге мы не можем включать ее в повышающую цепь, и, следовательно, использовать в алгоритме пометок.
, поскольку на следующем шаге мы не можем включать ее в повышающую цепь, и, следовательно, использовать в алгоритме пометок.
На втором шаге, аналогичном первому, точно таким же образом будем искать вторую повышающую цепь  , теперь уже для исходного потока
, теперь уже для исходного потока  .
.
Заметим, что мы теперь можем включать во вторую повышающую цепь  дуги обратные дугам
дуги обратные дугам  ,
,  и
и  , то есть дуги
, то есть дуги  ,
,  и
и  .
.
Пометив звездочкой вершину  , пометим из нее вершины
, пометим из нее вершины  и
и  . Затем из
. Затем из  пометим вершины
пометим вершины  и
и 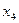 (вершина
(вершина  уже помечена).
уже помечена).

 (
( )
) 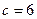

 (
( )
)







 *
* 





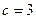

Рис. 7.  (
( )
) 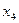 (
( )
)
Из  ничего не помечаем, так как вершина
ничего не помечаем, так как вершина  уже помечена. Просматриваем вершины
уже помечена. Просматриваем вершины  и
и 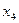 . Теперь из
. Теперь из  мы ничего пометить не сможем, поскольку дуга
мы ничего пометить не сможем, поскольку дуга  - насыщенная. Пометив из вершины
- насыщенная. Пометив из вершины 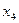 выход
выход  , заканчиваем алгоритм пометок и получаем повышающую цепь
, заканчиваем алгоритм пометок и получаем повышающую цепь  . Находим
. Находим 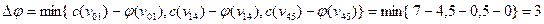 . Следовательно, новый поток
. Следовательно, новый поток  имеет вид
имеет вид


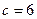
















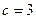

Рис. 7. 
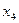
и 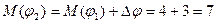 . Как обычно, на рисунке индексы опускаем.
. Как обычно, на рисунке индексы опускаем.
Построим теперь третью повышающую цепь  для потока
для потока  . Из вершины
. Из вершины  , пометим вершину
, пометим вершину  . Затем из
. Затем из  пометим вершину
пометим вершину  . Так как на дуге
. Так как на дуге  имеется положительный поток
имеется положительный поток  , то из вершины
, то из вершины  мы можем пометить вершину
мы можем пометить вершину  , используя обратную дугу
, используя обратную дугу 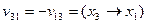 . Затем из
. Затем из  пометим вершину
пометим вершину 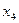 , а из нее пометим
, а из нее пометим  . Результат пометок представлен на следующем рисунке.
. Результат пометок представлен на следующем рисунке.
 (
( )
) 
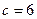

 (
( )
)







 *
*  (
(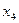 )
)





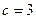

Рис. 8.  (
( )
) 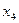 (
( )
)
Как обычно, начиная с конца  и выписывая в обратном порядке по очереди вершины
и выписывая в обратном порядке по очереди вершины 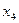 ,
, ,
, ,
, ,
, , из которых были нанесены пометки, получаем третью повышающую цепь
, из которых были нанесены пометки, получаем третью повышающую цепь 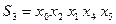 . Для нее определяем величину
. Для нее определяем величину 
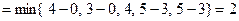 .
.
Здесь  в силу правила (1), поскольку
в силу правила (1), поскольку  и
и  .
.
Используя правило (2) пересчитываем величину потока на дугах  цепи
цепи 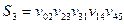 :
:  ,
,  ,
,  ,
,  ,
, 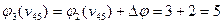 .
.
Остановимся подробнее на формуле  . Повысив величину потока на дугах
. Повысив величину потока на дугах  на
на 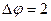 , мы затем, чтобы обеспечить условие неразрывности потока в вершине
, мы затем, чтобы обеспечить условие неразрывности потока в вершине  (сколько в нее «втекает», столько и «вытекает») вынуждены были уменьшить на ту же величину
(сколько в нее «втекает», столько и «вытекает») вынуждены были уменьшить на ту же величину 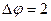 поток на дуге
поток на дуге  , поскольку
, поскольку 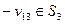 , то есть дугу
, то есть дугу  по цепи
по цепи  мы проходим в обратном направлении. Абстрактно это уменьшение «прямого» потока
мы проходим в обратном направлении. Абстрактно это уменьшение «прямого» потока  можно представлять себе как увеличение на те же 2 единицы «обратного» потока (на самом деле, разумеется, фиктивного, то есть не существующего в действительности), на (также не существующей реально) обратной дуге
можно представлять себе как увеличение на те же 2 единицы «обратного» потока (на самом деле, разумеется, фиктивного, то есть не существующего в действительности), на (также не существующей реально) обратной дуге  . Реальный поток на дуге
. Реальный поток на дуге  , конечно, равен алгебраической сумме «прямого» и «обратного» потоков. Поскольку величина обратного потока отрицательна и равна
, конечно, равен алгебраической сумме «прямого» и «обратного» потоков. Поскольку величина обратного потока отрицательна и равна  , то величина
, то величина  нового потока
нового потока 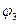 на дуге
на дуге  находится по приведенной выше формуле.
находится по приведенной выше формуле.
Особенно наглядный смысл имеют рассмотренные манипуляции для реальных потоков товаров. Так на первом шаге решения мы отправили  партии товара из пункта
партии товара из пункта  в пункт
в пункт  , а на третьем шаге «вернули» 2 из них обратно в
, а на третьем шаге «вернули» 2 из них обратно в  , заменив двумя партиями товара, доставленными из пункта
, заменив двумя партиями товара, доставленными из пункта  через
через  в
в  . Затем отправили обе возвращенные в
. Затем отправили обе возвращенные в  партии из пункта
партии из пункта  уже в пункт
уже в пункт 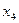 и далее в пункт назначения
и далее в пункт назначения  . В результате величина суммарного потока была увеличена на 2 партии.
. В результате величина суммарного потока была увеличена на 2 партии.
Полученный на третьем шаге результат представлен на следующем рисунке.


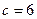













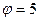
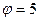

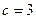

Рис. 9. 
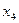
Мощность построенного потока 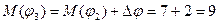 .
.
Попробуем построить повышающую цепь для потока  . Пометим звездочкой вершину
. Пометим звездочкой вершину  , из нее пометим
, из нее пометим  , из
, из  пометим
пометим  и, наконец, пометим
и, наконец, пометим  так же как и на предыдущем шаге. Очевидно, что больше ни одной вершины пометить не удастся, поскольку вершина
так же как и на предыдущем шаге. Очевидно, что больше ни одной вершины пометить не удастся, поскольку вершина  уже помечена.
уже помечена.
Лемма. Если с помощью алгоритма пометок невозможно поостроить повышающую цепь, то поток - максимальный и его мощность равна пропускной способности некоторого минимального разреза.
Доказательство. Построим такой разрез 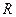 (он окажется минимальным), что
(он окажется минимальным), что  . Отметим на новом рисунке все помеченные вершины звездочкой и отдели
. Отметим на новом рисунке все помеченные вершины звездочкой и отдели м (входное)
м (входное)
 *
* 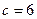

 *
*







 *
* 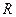



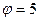
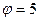

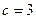

Рис. 9.  *
* 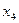
множество 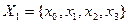 помеченных вершин от (выходного) множества
помеченных вершин от (выходного) множества  непомеченных вершин «линией» разреза
непомеченных вершин «линией» разреза 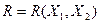 (разумеется такая линия существует, хотя и может быть изображена по разному). Покажем, что все разрезанные дуги
(разумеется такая линия существует, хотя и может быть изображена по разному). Покажем, что все разрезанные дуги  - насыщенные. Действительно, если дуга
- насыщенные. Действительно, если дуга  ненасыщенная, то выполняется условие
ненасыщенная, то выполняется условие  , причем вершина
, причем вершина 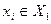 - помеченная. Но тогда с помощью алгоритма пометок из
- помеченная. Но тогда с помощью алгоритма пометок из 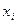 мы должны были пометить вершину
мы должны были пометить вершину 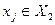 , которая по предположению непомечена. Полученное противоречие доказывает, что
, которая по предположению непомечена. Полученное противоречие доказывает, что  .
.
Пусть теперь  и
и  . Тогда поток
. Тогда поток  , поскольку иначе с помощью алгоритма пометок из помеченной вершины
, поскольку иначе с помощью алгоритма пометок из помеченной вершины  мы должны были пометить по обратной дуге вершину
мы должны были пометить по обратной дуге вершину  , которая по предположению непомечена. Таким образом,
, которая по предположению непомечена. Таким образом,  . Следовательно,
. Следовательно,  .
.
По следствию теоремы 2 поток  является максимальным, а разрез
является максимальным, а разрез 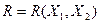 - минимальным. Что и требовалось доказать.
- минимальным. Что и требовалось доказать.
Замечание 3. В нашем случае в равенстве 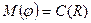 легко убедиться и непосредственно, поскольку
легко убедиться и непосредственно, поскольку  и
и  .
.
Теорема (Форд-Фалкерсон). Для любой сети с целыми пропускными способностями с помощью алгоритма Форда-Фалкерсона за конечное число шагов можно построить поток максимальной мощности, равной пропускной способности минимального разреза.
Замечание 4. Фактически эта теорема нами доказана лишь для частного рассматриваемого выше примера. Однако, все рассуждения нетрудно провести по аналогии и в общем случае, поскольку используемый алгоритм пометок очевидным образом применим к любой сети. На каждом шаге он либо приводит к пометке выхода  и, следовательно, к построению повышающей цепи и соответствующему повышению мощности потока на
и, следовательно, к построению повышающей цепи и соответствующему повышению мощности потока на 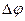 , либо оказывается, что выход невозможно пометить, и в этом случае, в силу доказанного выше утверждения поток оказывается максимальным и его мощность равна пропускной способности построенного (минимального) разреза. Если все пропускные способности дуг сети целые числа, то и величина
, либо оказывается, что выход невозможно пометить, и в этом случае, в силу доказанного выше утверждения поток оказывается максимальным и его мощность равна пропускной способности построенного (минимального) разреза. Если все пропускные способности дуг сети целые числа, то и величина  также целая, и, следовательно,
также целая, и, следовательно, 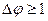 . Так как мощность потока ограничена (конечной) пропускной способностью произвольного разреза, то алгоритм закончится за конечное число шагов. Ч.т.д.
. Так как мощность потока ограничена (конечной) пропускной способностью произвольного разреза, то алгоритм закончится за конечное число шагов. Ч.т.д.
Замечание 5. Теорема Форда-Фалкерсона остается в силе и для произвольных соизмеримых (рациональных) пропускных способностей. Действительно,
приводя все дроби к общему знаменателю 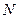 и принимая за новую единицу измерения величину
и принимая за новую единицу измерения величину 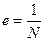 , мы получим сеть с целыми пропускными способностями.
, мы получим сеть с целыми пропускными способностями.
Замечание 6. В силу указанной теоремы корректно считать пропускную способность сети равной пропускной способности минимального разреза.
Замечание 7. Для иррациональных пропускных способностей алгоритм Форда-Фалкерсона также применим, но не обязательно приводит к результату за конечное число шагов. Поскольку на  -ом шаге
-ом шаге  , то последовательность
, то последовательность  возрастает. В силу ограниченности она сходится, причем, нетрудно показать, что в пределе получаем максимальный поток:
возрастает. В силу ограниченности она сходится, причем, нетрудно показать, что в пределе получаем максимальный поток:
 при
при  .
.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 2446; Нарушение авторских прав?; Мы поможем в написании вашей работы!