Свойства задачи линейного программирования

Прежде чем мы перейдем к перечислению свойств задачи линейного программирования рассмотрим понятия «выпуклая линейная комбинация точек» и «выпуклое множество точек».

Определение 1: Точка Х называется выпуклой линейной комбинацией точек Х₁,Х₂,…Х_n, если выполняются условия:

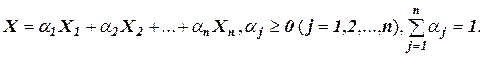
Очевидно, что при n=2 выпуклой линейной комбинацией двух точек является соединяющий их отрезок.

Определение 2: Множество точек называется выпуклым, если оно вместе с любыми своими двумя точками содержит их произвольную выпуклую линейную комбинацию.

Определение 3: Выпуклое замкнутое множество точек пространства (плоскости), имеющее конечное число угловых точек, называется выпуклым многогранником (многоугольником), если оно ограниченное, и выпуклой многогранной (многоугольной) областью, если оно неограниченное.

Пользуясь этими понятиями, мы можем представить выпуклый n -мерный многогранник как линейную комбинацию своих угловых точек.

Перечислим свойства задачи линейного программирования. Рассмотрим каноническую задачу, в которой система ограничений есть система уравнений. Для нее справедливы следующие утверждения:

1. множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым. Оно представляет собой многогранник или выпуклую многогранную область, которую в дальнейшем будем называть многогранником решений.

2. если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более чем в одной точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек.

3. каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка многогранника решений и, наоборот, каждой угловой точке многогранника решений соответствует допустимое базисное решение.

Как следствие всех свойств, мы получаем практический вывод: оптимум линейной функции задачи линейного программирования следует искать среди конечного числа её допустимых базисных решений.

Дата добавления: 2014-01-20