Геометрический метод решения задач линейного программирования

Геометрический метод – самый простой и наглядный методрешения задач линейного программирования. Он позволяет быстро и легко получить ответ. Но к сожалению, он имеет недостатки, не позволяющие применять его широко:

1. весьма ограниченная область применения (для двух неизвестных), что делает его бесполезным для практической работы;

2. многие величины, имеющие четкий экономический смысл (такие, как остатки ресурсов производства, избыток питательных веществ и т.п.) не выявляются при геометрическом решении задач.

Однако он исключительно полезен для понимания общих идей, лежащих в основе других методов решения.

Рассмотрим геометрический метод решения на примере. Пусть нам нужно решить следующую задачу: найти максимум функции F=2x₁-6x₂ при ограничениях: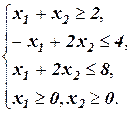

Нанесем на чертеж область допустимых решений задачи. Для этого на чертеж наносим прямые линии, отвечающие случаю равенства:

х₁+х₂=2; - х₁+2х₂=4; х₁+2х₂=8; х₁=0; х₂=0.

Каждая прямая делит плоскость на две полуплоскости. Полуплоскость, отвечающую нужному неравенству, выбираем подстановкой координат точек в соответствующее неравенство. Если после подстановки координат точки в неравенство оно становится верным, то нам нужна та полуплоскость, из которой была взята точка. Если же после подстановки координат точки в неравенство оно стало неверным, то нам нужна противоположная полуплоскость. В итоге получим выпуклый многоугольник ABCD, удовлетворяющий заданной системе неравенств.

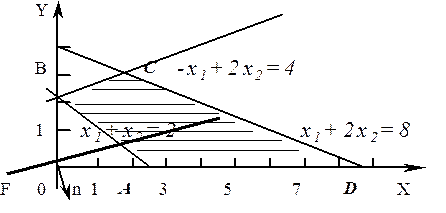
Рис.1.

Из множества точек ABCD нужно выбрать такую точку, для которой значение целевой функции F=2x₁-6x₂ будет наибольшим. Заметим, что графиком целевой функции будет прямая, перпендикулярная вектору 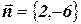, расположенная тем дальше от начала координат, чем больше значение F. Отсюда следует, что максимальное значение целевой функции будет достигаться в одной из угловых точек, а именно в той, через которую проходит прямая, перпендикулярная вектору 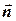и находящаяся на наибольшем удалении от начала координат в направлении вектора 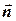. В данном случае это точка D (8,0). В этой точке достигается оптимальное (максимальное) значение целевой функции F=2x₁-6x₂ = 16.

Аналогично, минимальное значение целевой функции будет достигаться в одной из угловых точек, а именно в той, через которую проходит прямая, перпендикулярная вектору 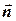и находящаяся на наибольшем удалении от начала координат в направлении противоположном вектору .

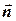Из рассмотренного графического способа решения задач линейного программирования на плоскости следует, что возможны, в зависимости от вида области допустимых решений, следующие случаи:

1. оптимальное решение единственно. Прямая F=F_max имеет одну общую точку с ОДР (рис.2, F – достигает максимума в точке С);

2. оптимальных решений бесконечное множество. Прямая F=F_max совпадает с одной из прямых ограничений. В этом случае каждая точка этой прямой является оптимальным решением (рис.3, F – достигает максимума в каждой точке отрезка ВС);

3. оптимального решения не существует по причине неограниченности целевой функции (рис.4);

4. оптимального решения не существует по причине противоречивости системы ограничений (ОДР является пустым множеством) (рис 5).

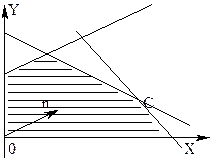
Рис.2 Рис.3

Рис.4 Рис.5

Если мы перефразируем свойства задач линейного программирования для данного метода, то получим:

1. оптимальное решение, если оно существует, лежит на границе ОДР;

2. если решение единственно, то оно достигается в одной из вершин ОДР;

3. если решений множество, они достигаются на одной из сторон выпуклого многоугольника ОДР (в том числе и в двух вершинах);

4. решение, лежащее в одной из вершин ОДР, является опорным, а сама вершина – опорной точкой.

5. для того, чтобы найти оптимальное решение, в принципе достаточно перебрать все вершины ОДР (опорные точки) и выбрать из них ту, где функция F принимает наибольшее значение.

Дата добавления: 2014-01-20