Шаг.Базисные переменные:х1, х2 и х5

Свободные переменные: х₃, х₄.

Выразим новые базисные переменные через свободные, начиная с разрешающего уравнения. Его далее используем для преобразования оставшихся уравнений системы.

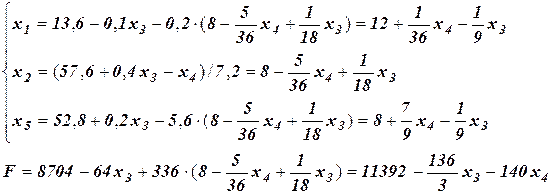
Положив свободные переменные равными 0, получим третье решение задачи: F=(12; 8; 0; 0; 8)=11392. Это значение оптимально, так как его увеличения нельзя достигнуть, не нарушив ограничений задачи.

Теперь можно в общем виде сформулировать критерий оптимальности решения при отыскании максимума целевой функции: если в выражении целевой функции через свободные переменные отсутствуют положительные коэффициенты при свободных переменных, то решение оптимально.

При определении минимума целевой функции Z возможны два пути:

1. отыскать максимум функции F, полагая F= -Z и учитывая, что

Z_min= -F_max;

2. модифицировать симплексный метод: на каждом шаге уменьшать целевую функцию за счет той свободной переменной, которая входит в выражение целевой функции с отрицательным коэффициентом. Критерий оптимальности решения при отыскании минимума целевой функции будет выглядеть следующим образом: если в выражении целевой функции через свободные переменные отсутствуют отрицательные коэффициенты при свободных переменных, то решение оптимально.

Дополнение: Сформулируем все возможные случаи, возникающие при оценке наибольших возможных значений переменных для перевода в симплексном методе свободных переменных в базисные. Обозначим х_i – переводимая свободная переменная, b_j - свободный член, a_ij – коэффициент при х_i. В общем виде уравнение х_j=b_j+…+ a_ijx_i+… определяет наибольшее возможное значение х_i по следующим правилам:

1. х_i=|b_j/a_ij|, если b_j и a_ij разного знака и ,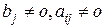

2. 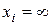, если b_j и a_ij одного знака и ,

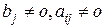3. х_i= 0, если b_j = 0и a_ij < 0,

4. 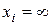, если b_j = 0и a_ij > 0,

5. 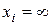, если a_ij = 0.

Симплексные таблицы.

При практических расчетах реальных задач удобно использовать симплексный метод реализованный в симплексных таблицах. Рассмотрим алгоритм их составления на примере конкретной задачи, не углубляясь в его подробное обоснование. Вернемся к задаче 1 (текст задачи см. лекция 29). Найти максимум функции 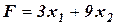при выполнении следующих условий:

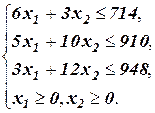
Приведем задачу к каноническому виду, добавив в каждое неравенство системы ограничений по балансовой переменной, указывающей величину остатков сырья соответствующего вида:

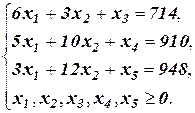
Выпишем матрицу и расширенную матрицу этой системы:

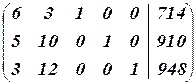
Их ранг равен 3, значит система совместна и имеет три базисные переменные. Общий вид таблиц следующий:

С	С1	С2	…	Сq	…	Cn
Базисные переменные	Сбаз	В	А1	А2	…	Аq	…	Аn
			a11	a12	…	a1q	…	a1n
			a21	a22	…	a2q	…	a2n
					…		…
			ai1	ai2	…	aiq	…	ain
					…		…
			am1	am2	…	amq	…	amn
				…		…
			…		…

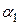
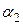
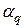
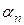
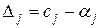
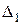
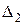
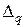
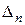
В первой строке этой таблицы указаны коэффициенты при переменных целевой функции. В столбцы А_j записывают коэффициенты при переменной х_j. В столбец В записывают свободные члены уравнений системы линейных ограничений. В первый столбец симплекс таблицы заносят наименования переменных, которые образуют единичный базис. Если такого базиса нет, то можно выбрать любые переменные в качестве базисных, при этом число базисных переменных равно рангу матрицы системы ограничений. Две последние строки таблицы предназначены для проверки полученного плана на оптимальность. Значения 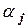вычисляются как скалярное произведение 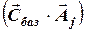. Значение целевой функции 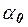на данном шаге можно вычислить так: . 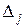Оценки переменных вычисляются по формуле .

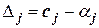Заполним первую симплексную таблицу для нашей задачи. В качестве трех базисных переменных выберем переменные х₃ , х₄ , х₅.

Таблица 1.

С
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5
x3
x4
x5

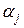
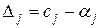
Проверяем выполнение критерия оптимальности (формулировку см.выше). В переложении для применения в симплексных таблицах возможны следующие варианты:

1. Если все оценки не положительны 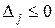, то найденный план оптимален, решение закончено.

2. Если имеются положительные оценки, например, 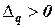, для которой все 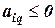, то целевая функция неограничена сверху на множестве планов и задача не имеет конечного решения.

3. Если столбцов описанных в пункте 2 нет, но имеется положительная оценка, то продолжаем решение, выбирая новый базис.

Для выбора нового базиса выделим наибольшую из положительных оценок. Пусть это будет 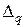. Назовем столбец с номером q – разрешающим. В этом столбце для положительных коэффициентов 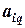составим отношения 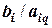, из которых выберем минимальное. Если оно получено в строке с номером p, (т.е. ), то эту строку назовем разрешающей. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент 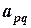. Новой базисной переменной вместо х_p будет переменная х_q. В нашей задаче наибольшая из положительных оценок «9» находится во втором столбце. Этот столбец будет разрешающим. Найдем разрешающую строку: 714/3=238; 910/10=91; 948/12=79. Минимальное значение – «79», значит третья строка будет разрешающей. Переходим к новой таблице по следующим правилам:

1. Заменим в первом столбце таблицы имя старой базисной переменной, стоящей в p -й строке (х_p= х₅ ), на имя новой базисной переменной согласно номеру разрешающего столбца (х_q= х₂ ).

2. В столбцах, соответствующих основным переменным, проставляем нули и единицы: 1 - против «своей» основной переменной, 0 - против «чужой» основной переменной.

3. Все элементы разрешающей строки делим на разрешающий элемент .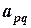

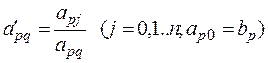
4. Далее производим пересчет остальных элементов симплекс-таблицы по методу Гаусса-Жордана. К каждой из остальных строк прибавляем преобразованную разрешающую строку, умноженную на такое число, чтобы в разрешающем столбце получился 0. Эти преобразования в виде формул можно записать так:

Таблица 2.

С
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5
x3			21/4				-1/4
x4			5/2				-5/6
x2			1/4				1/12
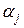
		9/4				3/4
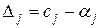
	3/4				-3/4

Анализ полученной таблицы 2 показывает, что решение не оптимально. Наибольшая (и единственная) из положительных оценок находится в первом столбце. Он будет разрешающим. Найдем разрешающую строку: 79:(1/4)=316; 477:(21/4)=90.9; 120:(5/2)=48. Минимальное значение – «48», значит вторая строка будет разрешающей. Базисная переменная х₄ меняется на переменную х₁. Переходим к следующей таблице по описанным выше правилам.

Таблица 3.

С
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5
х3						-2.1	1.5
х1						2/5	-1/3
х2						-0.1	1/6
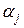
					0.3	0.5
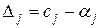
				-0.3	-0.5

Данные этой таблицы указывают на оптимальность полученного решения, согласно которому целевая функция достигает максимального значения 747 при х₁ = 48, х₂ = 67, х₃ = 225, х₄ = 0, х₅ = 0.

В случае, если при приведении задачи к каноническому виду не удается сразу получить базис, т.е. среди векторов-столбцов матрицы ограничений нет единичного вектора, содержащего 1 на i -ом месте, то используется М-метод или метод искусственного базиса. В левую часть i -ого уравнения добавляется новая переменная х_j, (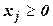). Она становится недостающей базисной переменной и вводится в целевую функцию с коэффициентом (-М), где М – очень большое положительное число (настолько большое, что все алгебраические суммы, в которые М входит с положительным коэффициентом – положительны, а все алгебраические суммы, в которые М входит с отрицательным коэффициентом – отрицательны). Такие переменные называют искусственными или М -переменными, а построенную задачу М -задачей.

Пример 1: Построить М -задачу: найти максимум функции F=-2x₁-3x₂-4х₃ при ограничениях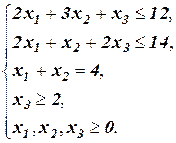

Преобразовав неравенства в равенства, получим следующую систему ограничений:

В матрице ограничений полученной задачи есть два единичных вектора-столбца: и 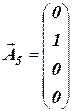. Чтобы получить еще два единичных вектора, введем две М -переменные х₇ и х₈ в третье и четвертое уравнения. В целевую функцию х₇ и х₈ вводим с коэффициентом (-М). Окончательно имеем следующую формулировку М -задачи:

найти максимум функции F= -2x₁ - 3x₂ - 4х₃ - Мх₇ - Мх₈ при ограничениях

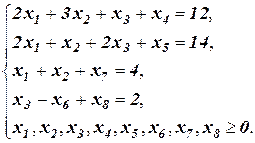
Решим эту задачу с помощью симплекс-таблиц так же, как решали каноническую задачу линейного программирования. Приведем все тре6уемые симплекс-таблицы без подробных комментариев.

Таблица 1.

С	-2	-3	-4				-М	-М
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5	А6	А7	А8
x4
x5
x7	-М
x8	-М							-1
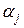
	-6М	-М	-М	-М			М	-М	-М
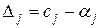
	М-2	М-3	М-4			-М

Таблица 2.

С	-2	-3	-4				-М	-М
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5	А6	А7	А8
x4									-2
x5				-1					-2
x1	-2
x8	-М							-1
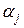
	-2М-8	-2	-2	-М			М	-2	-М
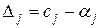
		-1	М-4			-М	-М+2

Таблица 3.

С	-2	-3	-4				-М	-М
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5	А6	А7	А8
x4									-2	-1
x5				-1					-2	-2
x1	-2
x3	-4							-1
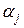
	-16	-2	-2	-4				-2	-4
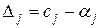
		-1				-4	-М+2	-М+4

Ответ: F (4,0,2,2,2,….)=16.

Возможен и другой принцип выбора уравнений для введения М -переменных. Они вводятся не сразу после приведения задачи к каноническому виду, а после получения первого базисного решения. Выбираются те уравнения, которые дают отрицательную компоненту в базисном решении и в каждое из них вводится новая неотрицательная искусственная переменная, которая имеет тот же знак, что и свободный член в правой части уравнения. В первой симплекс-таблице все искусственные переменные и обычные добавочные переменные, дающие неотрицательные компоненты базисного решения включаются в число базисных.

Пример 2: Построить М - задачу: найти максимум функции F=x₁+2x₂ при ограничениях:

.

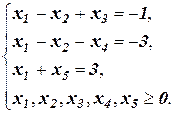Если мы возьмем в качестве базисных переменных х₁ и х₂, то получим недопустимое базисное решение Х=(0; 0; -1; 3; 5) с одной отрицательной компонентой, получающейся из первого уравнения. Введем в первое уравнение искусственную переменную у₁ с тем же знаком, что и свободный член. Также новую переменную введем в целевую функцию с коэффициентом (-М). Окончательно получим: найти максимум функции F=x₁ + 2x₂ - My₁ при ограничениях: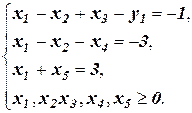

В обоих случаях дальнейшее решение задачи ничем не отличается от изложенного выше.

Дата добавления: 2014-01-20