Еріксіз электр тербелістері

Енді

.

Бұл формуланың оң жағын бірге тең 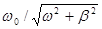шамаға көбейтсек, алатынымыз:

.

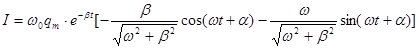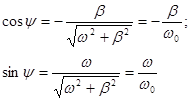
шарттарымен анықталатын y бұрышын енгізіп, ток күшін

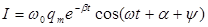(3.48)

түрінде жаза аламыз. Бұл жерде cosy<0, ал sіny>0 болғандықтан мәндері p/2 -ден p -ге дейін аралығында қамтылған. Сондықтан, контурда актив кедергінің болуына байланысты ток күші фаза жағынан кернеуді конденсаторда p/2-ден үлкен шамаға озып отырады. (3.45) функцияның графигі 3.4-суретте көрсетілген.

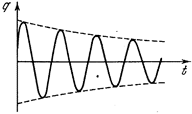
3.4-сурет. Зарядтың уақытқа тәуелділік графигі.

Кернеу мен токтың графиктері де осыған ұқсас. Тербелістің өшуін өшудің логарифмдік декрементімен сипаттау қабылданған.

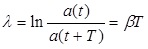, (3.49)

мұндағы а(t) қандай да бір шаманың амплитудасы (q, U, немесе І). Өшудің логарифмдік декременті амплитуда е есе азаятын уақыт ішіндегі N_e тербеліс санына кері екенін ескертеміз: l=1/N_e. (3.49) өрнек (b=R/2L) мәнін қойып және Т-ның орнына 2p/w ауыстырып, l үшін мына

l = 2pR/2L w = pR/Lw (3.50)

өрнегін аламыз. Жиілік w, демек l контурдың L,C,R параметрлерімен анықталады. Сонымен, өшудің логарифмдік декременті контурдың сипаттамасы болып табылады.

Еріксіз тербеліс болуы үшін, сырттан жүйеге периодты түрде әсер ету керек. Ол үшін контурдың элементтеріне тізбектей айнымалы ЭҚК немесе контурды үзіп оған айнымалы

U=U_m×coswt (3.51)

кернеу беру керек. Бұл кернеуді өздік индукцияның ЭҚК -не қосу керек. Нәтижесінде Ом заңы мына

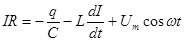(3.52)

түрге келеді. Мұны түрлендіріп келесі өрнекті аламыз:

. (3.53)

Мұндағы 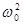(3.36) өрнегімен, β өшу коэффициенті R/2L өрнегімен анықталады. Бұл теңдеудің дербес шешімінің түрі

q = q_m× cos(wt -y) (3.54)

болады, мұндағы

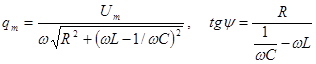. (3.55)

Егер дербес (3.54) шешімге біртекті теңдеуге сәйкес жалпы шешімді қосса, онда жалпы шешім болады. Уақыт t бойынша (3.54) өрнекті туындыласақ, контурдағы орныққан тербелістегі ток күшін табамыз:

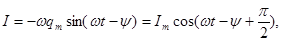
мұндағы 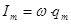деп белгіледік. Мұны мына түрде жазайық:

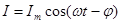(3.56)

мұндағы j=y-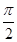ток пен берілген кернеудің арасындағы фаза ығысуы. (3.55) өрнегіне сәйкес:

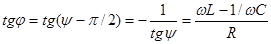. (3.57)

Бұл формуладан шығатыны - ток фаза жағынан кернеуден қалып отырады (j<0), егер wL>І/wC болса. (3.57) өрнегімен келіссек, онда:

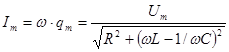. (3.58)

Енді (3.56) өрнегін мына түрде жазайық:

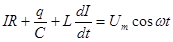(3.59)

ІR көбейтіндісі актив кедергідегі кернеуге U_R тең, 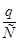– конденсатордағы кернеу U_C, L(dІ/dt) индуктивтіктегі кернеуді U_L анықтайды. Осыларды ескеріп, былай жазамыз:

U_R + U_C + U_L = u coswt, (3.60)

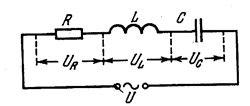әрбір уақыт мезетіндегі контурдың элементтеріндегі кернеулердің қосындысы сырттан берілген кернеуге тең (3.5-сурет).

3.5-сурет. Айнымалы ток тізбегі.

(3.60) өрнекке сәйкес:

U_R = RІ_m cos(wt - j). (3.61)

(3.54) өрнекті сыйымдылыққа бөліп, конденсатордағы кернеуді табамыз:

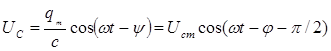, (3.6250)

мұндағы

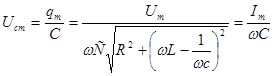. (3.6351)

(3.56) функциясының туындысын L-ге көбейтіп, индуктивтіктегі кернеуді табамыз:

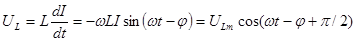, (3.64)

мұндағы

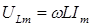. (3.65)

(3.60), (3.61), (3.62) және (3.64) өрнектерін салыстыра отырып, байқайтынымыз, сыйымдылықтағы кернеу ток күшінен p/2 фазаға қалып қоятынын, ал индуктивтіліктегі кернеу токтан p/2 фазаға озып отыратынын байқаймыз. Актив кедергіде кернеу мен ток бір фазада болады. Фазалардың қатынастарын векторлық диаграммада өте көрнекті етіп көрсетуге болады. Токтар осін, бастапқы фаза есептелетін түзу ретінде алайық. Онда 3.6-суреттегі диаграмманы аламыз. (3.65) өрнекке сәйкес U_R, U_C, U_L қосындылары тізбекке берілген U кернеуді беруі керек.

3.6-сурет. Сыйымдылық, индуктив және актив кернеулерінің векторлық диаграммасы.

Сондықтан диаграммадағы U, әрбір U_R, U_C, U_L векторларының қосындысы түрінде көрсетілген.

Дата добавления: 2014-01-20