Френель зоналары

Изотропты біртекті ортада S нүктелік жарық көзінен таралатын сфералық толқынның Р нүктесіне келіп түскен жарық тербелістерінің амплитудасын анықтайық (6.2-сурет). Мұндағы S толқын беттері Р түзуімен салыстырғанда симметриялы. Толқын бетін сақиналық аудандар - Френель зоналарына бөлейік, ол үшін центрі бір осьте жатқан шеңберлер жүргізейік. Шеңберлерден Р нүктесіне дейінгі қашықтықтарды бір-бірінен жарты толқын ұзындығына l/2-ге артық болатындай етіп салайық.

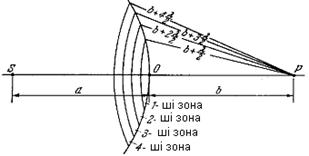
6.2-сурет. Френель зоналары.

Суретте көрсетілгендей, m-ші зонаның сыртқы шетінен Р нүктесіне дейінгі қашықтық b _m мынадай:

b _m = b + ml/2, (6.3)

мұндағы b − толқын бетінің О төбесінен Р нүктесіне дейінгі қашықтық. Екі көрші зонадан Р нүктесіне келіп жететін тербелістер қарама-қарсы фазада болады. Сондықтан да әр зонадан келіп түскен толқындардың көрші зонадан түскен толқындармен фаза айырымы p- ге тең болады.

Френель зоналарының ауданын есептейік. m-ші зонаның сыртқы шекарасы толқын бетінде биіктігі h_m сфералық сегмент құрайды (6.3-сурет).

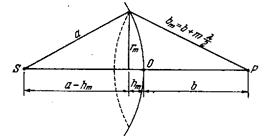
6.3-сурет. Френелдің m -ші зонасы.

Бұл сегменттің ауданын S_m деп белгілейік. Онда m-ші көршілес екі зонаның ауданданының айырымы мынадай:

ΔS_m = S_m - S_m-1,

мұндағы S_m-1 − (m-1)-ші зонаны айқындайтын сфералық сегментінің ауданы. 6.3-суреттен Пифагор теоремасына сәйкес:

,

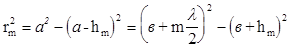(а − толқын бетінің радиусы, r_m − m-ші зонаның сыртқы шекарасының радиусы). Теңдеуді түрлендірсек:

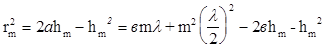, (6.4)

бұдан 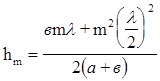. (6.5)

Түрлендіру кезінде, m -нің бастапқы мәндері үшін l -ның аз шама екенін ескеріп, l² бар қосындыны ескермейміз. Онда (6.5) өрнек

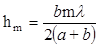(6.6)

болады. Сфералық сегмент ауданы S = 2pRh -қа тең (R – сфера радиусы, h – сегмент биіктігі). Олай болса(6.3-суреттен R= a)

, (6 7)

мұндағы S_m – m-ші зонаның ауданы. Френель зоналарының өсімшесі (көрші зоналардың өзгерісі):

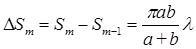. (6 8)

Бұл ΔS_m m -ге тәуелді емес. Бұл онша үлкен емес m үшін Френель аумақтарының аудандары шамамен бірдей екенін көрсетеді.

(6.4) өрнегінен зонадан радиусын тапсақ, онда 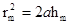екенін көреміз. (6.6)-теңдеуге h_m үшін мәнін қойып, m-ші Френель зонасының сыртқы шекарасы радиусының өрнегін табамыз:

. (6.9)

Жарық көзі өте алыста орналасса, яғни а ® ¥, онда (6.9) етеңдеуінен келесі өрнек шығады:

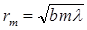. (6.10)

Бұл өрнек (6.10) жазық толқын үшін Френельдің m-ші зонасыныңа радиусы. а = в= 1 м және l=0,5 мкм деп алатын болсақ, бірінші зонаның радиусы r₁=0,5 мм екенін көреміз. Сондықтан, бірінші зонадан басқа барлық зоналардан түскен толқындардың интерференциясының нәтижесі нолге дейін әкеледі және S - тен Р нүктесіне жарық ағыны S Р жіңішке тар канал ішімен түзу сызықты жүретіндей болады. Сондықтан, Гюйгенс-Френельдің толқындық принципі біркелкі ортада жарықтың түзу сызықты таралуын түсіндірді. Келесі зоналардың радиусы 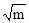-дей өседі. Сонымен, Френель зоналарының аудандары шамамен бірдей болады.

Қорытқы амплитуданы есептеуге арналған Френель зоналары тәсілі төмендегідей қорытындыларға әкеледі:

1) Толқын шебінің (фронтының) толық ашық жағдайында қорытқы толқынның интенсивтілігі осы нүктеде тек қана бірінші Френель зонасы туғызған интенсивтіктің 1/4 бөлігіне тең болады.

2) экрандағы дөңгелек тесіктің ауданы тек қана бірінші Френель зонасы сиятындай етіп алынса, бақылау нүктесінде интенсивтік толық ашық фронт интенсивтігінен салыстырғанда төрт есе көп болады.

3) Егер барлық жұп (не барлық тақ) Френель зоналарын жапса, онда қорытқы амплитуда Е₀=E₁+Е₃+E₅+... (не Е₀=E₂+Е₄+E₆+...) болады, яғни интенсивтік артады.

4) Егер барлық жұп (не барлық тақ) алаңшалардың фазаларын қарама-қарсы фазаға өзгертсек, онда Е₀=E₂+Е₄+E₆+... болады, яғни өте үлкен интенсивтік артауы болады.

6.3 Қарапайым бөгеттерден алынған Френель дифракциясы

Дөңгелек тесіктен алынатын дифракция. Сфералық толқынның жолына радиусы r₀ дөңгелек тесік ойып алынған мөлдір емес экран қояйық.

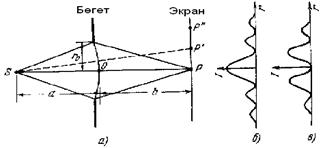
6.4-сурет. Дөңгелек саңылаудағы жарық дифракциясы.

6.4 а -суретте а − S жарық көзінен бөгетке дейінгі қашықтық, b − бөгеттен Р нүктесіне дейінгі қашықтық, мұнда r₀<< a, b. Егер a мен b қашықтықтары мына қатынасты қанағаттандырса

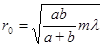, (6.9)

мұндағы m - бүтін сан, онда тесік Р нүктесі үшін орнатылған m -ға тең алғашқы Френель зоналарын ашық қалдырады. Сондықтан, ашық Френель зоналарының саны мына өрнекпен анықталады:

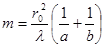. (6.10)

Р нүктесіндегі барлық зоналардан қозған қорытқы тербелістердің амплитудасы

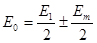(6.11)

болады, мұндағы плюс таңбасы тақ m-ға және минус таңбасы жұп m-ға сәйкес келеді. Кіші m-дер үшін амплитуда Е_m мәні Е₁ -ден аз ғана өзгеше болады. Тақ m-дерде Р нүктесіндегі амплитуда Е₀=Е₁, ал жұп m-дерде Е₀=0 болады. Бөгетті алып тастағанда Р нүктесіндегі амплитуда Е₀=Е₁/2 болады. Сонымен, аз ғана тақ санды зоналарды ашатын бөгет амплитуданы екі есеге жуық, ал интенсивтікті - төрт есеге жуық арттырады. Сондықтан, дөңгелек тесіктен алынатын дифракциялық бейне центрі Р нүктесінде болатын кезектескен қара және жарық сақина түрінде болады (егер m жұп болса, центрде қара нүкте, ал m тақ болса ақ нүкте болады), интенсивтік максимумы бейне центрінен қашықтық бойынша азаяды (6.4 б,в- суреттерді қараңыз).

Дөңгелек дискіден алынатын дифракция. Жарық көзі S пен бақылау нүктесі Р арасына радиусы r₀ (6.5-сурет) мөлдір емес дөңгелек диск қояйық. Егер диск m алғашқы Френель зонасын жапса, Р нүктесіндегі амплитуда

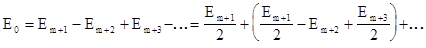
болады. Жақша ішіндегі өрнектерді нөлге тең деп алуға болады, олай болса,

Е₀ = Е_m+1 /2. (6.12)

(6.12) өрнегі бойынша, дөңгелек мөлдір емес дискіден алынатын дифракцияда экранның центріндегі (Р нүктесіндегі) интенсивтік нөлден өзгеше болады.

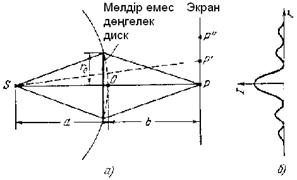
6.5-сурет. Дөңгелек дискідегі жарық дифракциясы.

Сонымен, дифракциялық бейне кезектескен жарық және қараңғы концентрлік сақиналар түрінде болады. Бейненің центрінде бірінші ашық Френель зонасының жартысына сәйкес келетін максимум болады (ақ дақ - Пуассон дағы). Максимумдер интенсивтігі бейне центрінен қашықтық бойынша азаяды (6.5 б -сурет). Дискінің радиусы өскен сайын бірінші ашық Френель зонасы Р нүктесінен алыстайды және осы зона бетіне нормаль мен Р нүктесіне бағыт арасындағы бұрыш ұлғаяды. Нәтижесінде орталық максимумның интенсивтігі диск мөлшері үлкейген сайын азаяды. Үлкен мөлшерлі дискіде оның арғы жағында көлеңке болады, оның шекарасы маңында өте нашар дифракциялық бейне орын алады. Бұл жағдайда жарық дифракциясын елемей, жарықты түзу сызықты таралады деп есептеуге болады.

6.4 Бір саңылаудан алынатын Фраунгофер дифракциясы

Жазық монохромат жарық толқынының ені в саңылаудағы дифракциясын қарастырайық. Ұзындығы l жарық толқыны саңылау жазықтығына нормаль бағытта түссін (6.6-сурет). Параллель жарық шоғы мөлдір емес Э₁ экрандағы саңылаудан өтіп, сәулелердің бастапқы түсу бағытының оң және сол жағына әртүрлі бұрыштармен дифракцияға түседі. Линза Л дифракцияға түскен параллель жарық шоқтарын, оның фокус жазықтығында орналасқан Э₂ экранда жинайды. Дифракцияланбаған сәулелер В₀ нүктесіне, ал дифракцияға түскен сәулелер j бұрышымен В_j нүктесіне жиналады. Саңылау жазықтығына параллель жарық шоғы нормаль түрде түскендіктен, толқын шебі (фронты) саңылау жазықтығымен бірдей болады, яғни саңылау жазықтығында толқын шебінің барлық нүктесі бірдей фазамен тербеледі. Саңылау жазықтығындағы толқын шебін саңылау шеттеріне параллель бірдей ені бар жолақтарға бөлейік. Әрбір жолақ екінші реттік жарық көзі болады. Экрандағы жарық амплитудаларын екі түрлі тәсілмен − графикалық және аналитикалық тәсілдермен шешуге болады.

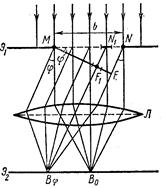
6.6-сурет. Бір саңылаудағы Фраунгофер дифракциясы.

6.5 Екі саңылаудан(дифракциялық тордан) алынатын жарық дифракциясы

Ендері b, бір-бірінен а қашықтығында орналасқан екі саңылауға жарықтың параллель шоғын түсірейік (6.7-сурет).

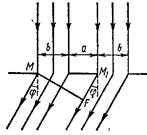
6.7-сурет. Дифракциялық тордағы жарық дифракциясы.

Саңылаулар, жарық шашпайтын бағыттарда нолдік мәнді интенсивтігі бар минимумдар болады. Максимумдарға келетін болсақ, бір саңылауда байқалған бағыттардың барлығында бірдей олар байқалмайды. Екі саңылау тараған жарық сәулелерінің өзара интерференциясы нәтижесінде кейбір бағыттарда олар өзара жойылады. Сондықтан, бір саңылаудан алынған дифракциядан өзгеше, екі саңылау жағдайында қосымша максимумдар пайда болады. Нолдік интенсивтігі бар қосымша максимумдар сәулелердің оптикалық жол айырымы l/2, 3l/2, 5l/2,... болатын нүктелерден шығатын (мысалы, саңылаулардың шеткі сол М және М₁ нүктелері) бағыттарда байқалады, яғни

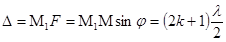, (k=1,2,3,...).

Егер 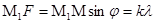болса, онда бір саңылау әсерінен екінші саңылау күшейтіледі. Егер а+в =d болса, қосымша минимумдар мен бас максимумдар шарты былай жазылады:

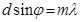(бас максимумдар) (m=0,1,2,…) (6.13)

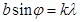(бас минимумдар) (k=1,2,3,...) (6.14) 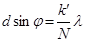(қосымша минимумдар) (6.15)

,

яғни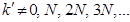

6.6 Дифракциялық тор

Қарапайым бір өлшемді дифракциялық тор деп ендері бірдей, біріне-біріне параллель, бір жазықтықта орналасқан өте көп N бірдей саңылаудан тұратын (олар бір-бірінен ені бірдей мөлдір емес жолақтармен бөлінген) жүйені айтады. Саңылау енін в, қара жолақ енін а деп белгілейік.

d= а+в мәні дифракциялық тордың периоды деп аталады. Бір саңылаудан алынатын Фраунгофер дифракциясы сияқты, дифракция бұрышы бойынша дифракциялық тордың интенсивтігін графикалық және аналитикалық түрде өрнектеуге болады. Дифракциялық тордың интенсивтігінің бас максимум шарты төмендегі өрнекпен анықталады

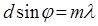, (m=0,1,2,3,...) (6.16)

мұндағы m − бас максимумдар реті. Нолдік ретті максимум біреу, 1 -ші, 2 -ші және т.б. ретті максимумдар екіден болады.

6.7 Дифракциялық тор - спектрлік аспап

Дифракциялық тор, оған түсетін жарықты максимумның бұрыштық жағдайы толқын ұзындығына тәуелді кезде, спектрге жіктейді. j=0 болғанда барлық толқын үшін максимум болады. m -реті максимумдардың бұрыштық жағдайы m>1 кезде әртүрлі толқын ұзындығы үшін әртүрлі болады. Ол 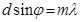максимум шартынан шығады. Мына шама бұрыштық дисперси я деп аталады

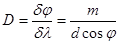. (6.17)

Бұдан m максимум ретінің өсуімен тор периодының d азаюы нәтижесінде дисперсия артады.

Үлкен санды бұрыштық дисперсия толқын ұзындығы жақын спектрлік сызықтарды ажыратуға, оларды жеке сызықтар ретінде байқау мүмкіндіктерін береді.

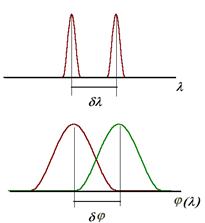
6.8-сурет. Жарықтың спектрлік аспаптан өткеннен кейінгі спектрлік сызықтарының ені.

Спектрде толқын ұзындықтары жақын l₁ мен l₂, жұп екі сызығы берілген, осы толқын ұзындықтарының айырмасы dl = l₂ - l₁ болатын екі сызық болсын. Кез-келген сызық «табиғи» ұзындыққа ие болады dl₁» dl₂ < dl. Әрбір сызық ені нолге тең болғанда да, дифракция торынан кейін оған жолақ сәйкес келеді (6.8-сурет, төменгісі). Ол тор қасиетімен анықталып, толқын ұзындықтары жақын болатын сызықтар үшін Ddl=dj -ден аз, не оған тең болуы қажет.

Спектрлік аспаптың ажырату күші

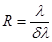. (6.18)

Бұл өрнекте dl − спектрде жеке сызықтар ретінде байқалатын сызықтардың толқын ұзындықтарының минимал айырымы, R − спектрлік аспапты (дифракциялық торды) сипаттайтын шама.

Нег. 2[381-427], 7[361-375], 8[322-347].

Қос. 48[316-330].

Бақылау сұрақтары:

1. Гюйгенс принципінің және Гюйгенс-Френель принципінің анықтамасын беріңіз.

2. Френельдің зонасы әдісін түсіндіріңіз.

3. Френель дифракциясы мен Фраунгофер дифракциясының арасында қандай айырмашылық бар?

7-дәріс

Заттағы электромагниттік толқындар

7.1 Жарық дисперсиясы

Жарықтың дисперсиясы деп заттың сыну көрсеткішінің толқын ұзындығына тәуелділігін айтады. Дифракциялық және призмалық спектрлердегі ерекшеліктерге тоқталайық.

1. Дифракциялық тор түскен сәулені оның толқын ұзындықтары бойынша тікелей ажыратады, дифракциялық максимумдарға сәйкес пайда болған бағыттарының бұрыштарын өлшеп, толқын ұзындығын есептеуге болады. Призма, түскен жарық шоғын сыну коэффиценттері бойынша жіктейді. Сондықтан жарық толқынының ұзындығын анықтау үшін призма арқылы жасалған заттың n=f(l) тәуелділігін білу керек. n=f(l) графигін дисперсия қисығы деп атайды. Толқын ұзындығын бұл қисықтықтан емес, призмалық спектрографтың белгілі спектрлерін градуирлеу арқылы есептейді.

2. Спектрлердегі құраушы түстердің орналасу тәртібі призма мен дифракциялық торда әртүрлі болады. Дифракциялық тор үшін ауытқу бұрышының синусы толқын ұзындығына пропорционал болады да, ауытқу бұрышы толқын ұзындығы өскен сайын артады. Нәтижесінде қызыл сәулелер (үлкен толқын ұзындығы бар) дифракциляқ торда күлгін сәулелерге қарағанда күштірек ауытқиды. Призма сәулелерді спектрге сыну коэффициенті бойынша жіктейді. Қызыл сәулелердің сыну коэффициенті күлгін сәулелерге қарағанда аз болғандықтан, призма оларды күлгін сәулелерге қарағанда нашар ауытқытады.

Спектрлік құрамды призмалық спектрограф көмегімен анықтаудың кемшіліктеріне (градуирлеу жасау, спектр бөлігінің әр жерінде әртүрлі дисперсия) қарамастан, олар спектрлік талдау мақсатында кеңінен қолданылады. Призманы жасау дифракциялық торға қарағанда едәуір оңайырақ, соған қоса призмалық спектрографта үлкен жарық күшін алуға болады. 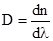шамасы заттың дисперсиясы деп аталады, ол толқын ұзындығы бойынша сыну көрсеткішінің өзгеру жылдамдығын көрсетеді. 7.1-суретінен – мөлдір заттар үшін сыну көрсеткіші толқын ұзындығы азайған сайын монотонды түрде өседі, сондықтан 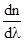модуль бойынша l кеміген сайын артады. Мұндай дисперсия нормаль дисперсия деп аталады. Егер зат сәулелердің бөлігін жұтатын болса, онда жұту аймағы мен оның маңында дисперсия жүруі аномальді түрде болады, сондықтан ол аномаль дисперсия деп аталады.

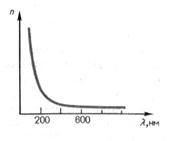
7.1-сурет. Сыну көрсенткішінің толқын ұзындығына тәуелділігі.

7.2 Жарық дисперсиясының электрондық теориясы

Максвелдің макроскопиялық электромагниттік теориясы бойынша ортаның абсолют сыну көрсеткіші , мұндағы e − ортаның диэлектрлік өтімділігі, m − ортаның магнит өтімділігі. Барлық зат үшін спектрдің оптикалық аумағында m=1, сондықтан

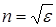. (7.1)

Жарықтың электрондық теориясын біртекті диэлектрикке қолданайық; жарық дисперсиясы e-нің жарық толқындарының жиілігін 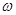тәуелді салдары деп ойлайық. Анықтама бойынша заттың диэлектрлік өтімділігі

ε=1+æ=,

мұндағы æ– ортаның диэлектрлік сезімталдығы, e₀ – электр тұрақтысы, Р – поляризацияланудың лездік мәні. Олай болса

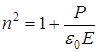. (7.2)

Бірінші жуықтауда еріксіз тербелістерді көбіне ядромен нашар байланысқан, тек сыртқы электрондар – оптикалық электрондар жасайды деп есептеуге болады. Бір оптикалық электрон тербелісін қарастырайық.

Еріксіз тербеліс жасайтын электронның дипольдік моменті р=ех, мұндағы е – электрон заряды, х – жарық толқынының электр өрісі әсерінен электрон ығысуы. Диэлектриктегі атомдар концентрациясы n₀ болса, онда поляризацияланудың лездік мәні

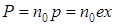. (7.3)

(7.2) мен (7.3)-тен

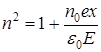. (7.4)

Электромагниттік толқындардың затқа әсері кезінде өріс кернеулігі

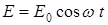(7.5)

болады. Электронның еріксіз тербеліс теңдеуі (кедергі күшін елемегенде) мына түрде жазылады:

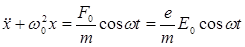, (7.6)

мұндағы 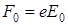– толқын өрісі тарапынан электронға әсер етуші күштің амплитудалық мәні, 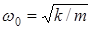– электрон тербелісінің меншікті жиілігі, m - электрон массасы.

(7.6)-теңдеуінің шешімін мына түрде жазуға болады

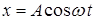. (7.7)

мұндағы

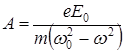. (7.8)

(7.7) және (7.8) теңдеулерін (7.4) теңдікке қойсақ:

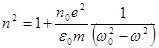. (7.9)

Егер затта әртүрлі меншікті жиілікті 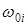, еріксіз тербелістер жасайтын әртүрлі е_і зарядтар болса, онда

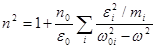. (7.10)

мұндағы m_і – і-ші заряд массасы. Соңғы теңдеулерден көретініміз: сыну көрсеткіші n сыртқы өріс жиілігіне w тәуелді, бұл жарық дисперсиясы құбылысының дәлелі болады.

7.2-суретінде n -нің w -ға тәуелділігі көрсетілген, АВ – аномаль дисперсия аумағы (n кемиді w -нің өсуі кезінде), n -нің w -ге тәуелділігінің басқа бөліктері нормаль дисперсияны суреттейді (n өседі w -ның өсуі кезінде).

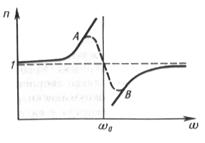
7.2-сурет. Сыну көрсеткішінің жиілікке тәулділігі.

7.3 Жарықтың жұтылуы

Жарықтың жұтылуы (адсорбциясы) деп зат арқылы өткен жарық толқынының толқын энергиясының басқа түрге түрлену салдарынан, энергия жоғалту құбылысын айтады. Нәтижесінде жарық арқылы өткенде интенсивтік азаяды.

Заттағы жарық жұтылуы Бугер заңымен бейнеленеді:

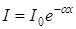, (7.11)

мұндағы І₀ мен І – жазық монохромат жарық толқынының қалыңдығы х жұту затына кірудегі және шығудағы интенсивтіктері, a – жарық толқынының ұзындығына, химиялық табиғатына және зат күйіне тәуелді жұту коэффициенті; ол жарық интенсивтігіне тәуелді емес. (7.11)-ді дифференциалдап мынаны аламыз:

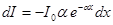. (7.12)

Бұдан – интенсивтіктің dx жолындағы азаюы, осы жол ұзындығына және интенсивтік мәніне пропорционал. (7.11)-ден х=1/a кезінде интенсивтік І мәні І₀ -ден е есе аз болатынын көреміз. Жұту коэффициенті жарық интенсивтігі е есе азаятын қабат қалыңдығынан өткенде, оған кері шама болатынын көреміз.

Жұту коэффициенті толқын ұзындығына l тәуелді, ол әртүрлі зат үшін әртүрлі шама. Мысалы, біратомды газдар мен металл буларының жұту коэффициенті нольге жақын; тек қана өте тар спектрлік аумақтарда (шамамен 10^-12-10^{-11 м) өткір минимумдар болады (сызықты жұту спектрі). Бұл максимумдар электрондардың атом ішіндегі тербелістерінің резонанс жиілігіне сәйкес келеді. Молекулалардағы атомдардың тербелістерімен анықталатын молекулалардың жұту спектрі жұту жолақтарымен сипатталады (10-10}-10^{-7 м). Диэлектриктер үшін жұту коэффиценті аз шама (10-3}-10^-5 см^-1), бірақ оларда жарықты кейбір толқын ұзындығы интервалында селективті түрде жұтуы болады, a кенет өседі, жұтудың кең аумақтары байқалады, яғни диэлектриктер тұтас жұту спектріне ие болады. Жоғары қысымдағы газдар, сондай-ақ сұйық пен қатты денелер кең жұту жолақтарына ие болады.

Металдар жарық үшін мөлдір зат емес (жұту коэффициенті ~10⁶ м^-1). Ол металдарда еркін электрондардың болуымен түсіндіріледі. Жарық толқындарының электр өрісінің әсерінен еркін электрондар қозғалысқа түседі – металдарда, джоуль жылуын бөлетін шапшаң айнымалы өзгеретін токтар пайда болады. Жарық толқынының энергиясы металдың ішкі энергиясына өтуі нәтижесінде тез азаяды. Металдың өткізгіштігі көп болған сайын, ондағы жарықтың жұтылуы көп болады. Жұтатын денелердің түрлі-түсті болулары жұту коэффициентінің толқын ұзындығына тәуелділігімен түсіндіріледі. Шыны, мысалы, қызыл және қызғылт сары сәулелерді нашар жұтып, жасыл мен көк сәулелерді күшті жұтады, ал енді шыныға ақ жарықты түсіргенде ол қызыл түсті болып көрінеді. Егер осындай шыныға жасыл және көк жарықты түсірсек, бұл толқын ұзындығындағы жарықты күшті жұтуы себебінде қара түсті сияқты болады. Бұл құбылыс жарық фильтрлері өндірісінде қолданылады.

7.4 Поляризацияланған және поляризацияланбаған жарық. Малюс заңы

Егер жарық векторының бағыттары қандай да бір тәсілмен реттелген болса, онда жарық поляризацияланған деп аталады,

Кәдімгі жарықта бұл бағыттар тұрақты түрде өзгереді. Мұндай жарық поляризацияланбаған жарық болып табылады.

Жарық поляризациясын қалай бақылауға болады? Жарықты 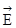векторының кейбір бағытымен ғана өткізетін құралдар болады (оларды поляризаторлар немесе анализаторлар деп атайды). Жарық поляризацияланбаған болса, анализаторды горизонталь осі маңында бұрғанда фотоқабылдағыштағы жарық интенсивтігі өзгермейді: электр векторының тербеліс амплитудасы өзгермейді. Егер поляризацияланбаған жарықты поляризатор арқылы өткізсе, онда өткен жарық сызықты немесе жазықполяризацияланған болады. (7.3-сурет)

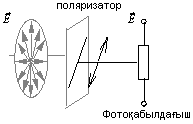
7.3-сурет. Поляризацияланған жарықту алу сұлбасы.

Мұндай жағдай үшін поляризация дәрежесі деген ұғым енгізіледі.

Поляризация дәрежесі келесі өрнек арқылы анықталады:

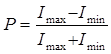. (7.13)

Электр өрісі кернеулік 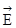векторының тербеліс амплитудалары поляризация жазықтығында үлкен мәнге ие болады. Мұндай жағдайда I_min=0 болып, ал поляризация дәрежесі бірге тең болады, яғни Р=1. Табиғи жарық үшін I_max=I_min және Р=0.

Жазық поляризацияланған жарық үшін Малюс заңы орындалады. Электр векторының тербелістері вертикаль жазықтықта және тербеліс амплитудасы Е₀ болсын. Анализатор осі поляризация бағытымен алғанда φ бұрышқа бұрылған болса, фотолқабылдағышқа мынадай амплитудалы жарық (7.4-сурет) келіп жетеді

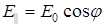. (7.14)

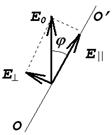
7.4-сурет. Тербеліс амплитудасының Е₀ анализатор осіндегі проекциясы.

Суреттен жарық векторының перпендикуляр бағытағы проекциясы нөлге тең, өйткені ол бағыттағы жарық анализатордан өтпейді.

Интенсивтілік амплитуда квадратына тура пропорционал I~E² болғандықтан, келесі өрнекті оңай аламыз:

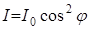, (7.15)

мұндағы I ₀ – поляризацияланған жарық интенсивтігі, I – анализатордан өткен жарықтың интенсивтігі, φ – поляризатор мен анализатор остерінің арасындағы бұрыш.

Жоғарыдағы өрнектегі I ₀ поляризацияланған жарықтың интенсивтігін I _р деп, ал I анализатордан өткен жарықтың интенсивтігін I _А деп белгілейік. Онда (7.15) өрнекті мына түрде жазамыз:

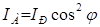. (7.16)

(7.16) өрнегі Малюс заңы деп аталады.

Егер табиғи жарықты поляризация жазықтықтары φ бұрыш құрайтын екі поляроидтан өткізсек, біріншісінен жазық поляризацияланған жарық интенсивтігі 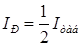шықса, екіншісінен (7.16)-ке сәйкес интенсивтігі 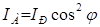жарық шығады. Сондықтан екі поляроид арқылы өткен жарық интенсивтігі мынаған тең:

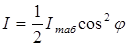. (7.17)

Бұдан 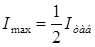, φ =0 (поляроидтар параллель) және 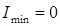, (поляроидтар перпендикуляр) болады.

7.5 Жарықтың шағылу мен сыну кезіндегі поляризациясы. Брюстер заңы

Жарық толқыны екі орта шекарасынан өткенде, жарық толқынының жартылай шағылуы болады. Шағылған сәуле нормальмен түсу бұрышына тең шағылу бұрышын түзіп, түсу жазықтығында жататындай бағытта болады.

Шағылған жарықтың интенсивтігі поляризация күйіне тәуелді болатындықтан, әртүрлі тәсілмен поляризацияланған жарық орта шекарасынан әртүрлі интенсивтікпен шағылады, шағылған жарық жартылай поляризацияланған болады (7.5-сурет).

7.5-сурет. Шағылу және сыну кезіндегі жарықтың поляризациялану сұлбасы.

Поляризация дәрежесі түсу бұрышына тәуелді. Мына жағдайда

(7.18)

tg (і+r)=¥және І_|| =0, яғни шағылған жарықта тек қана түсу жазықтығына перпендикуляр тербелістер болады. Шағылған толқын толық поляризацияланған болады. 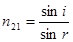және (7.18) шартынан келесі өрнекті аламыз:

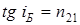. (7.19)

(7.19) өрнегі Брюстер заңы деп аталады. Шағылған жарықта тек қана түсу жазықтығына перпендикуляр поляризацияланған толқын болады, і = і_Б бұрышы толық поляризация бұрышы не Брюстер бұрышы деп аталады.

7.6 Жарықтың қосарлана сынуы

Әртүрлі сыну көрсеткіші бар екі ортада сәуленің қосарланып сынуы болады. Кристалл осі сәуленің түсу жазықтығына перпендикуляр болсын делік Кәдімгі поляризацияланбаған жарық кристалға енгенде кәдімгі және кәдімгі емес сәулеге бөлінеді. Олардың сыну көрсеткіштері әртүрлі, сондай-ақ сыну бұрыштары да әртүрлі. Сынған сәулелер поляризацияланған болады: кәдімгі сәуленің поляризация жазықтығы сурет жазықтығымен бірдей болады, поляризация бағыты кристалл осіне перпендикуляр болады.

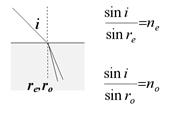
7.6-сурет. Жарық сәулесінің қосарлана сынуы.

Енді күрделі жағдайды қарастыралық: оптикалық ось бетке кейбір бұрышпен бағытталсын. Сурет жазықтығына перпендикуляр поляризация бағыты бар сәуле кәдімгі болады. Кәдімгі сәулелердің сәулелік беттерінің қималары шеңбер болады да, ол кристалдан сынбай өтеді (7.7-сурет).

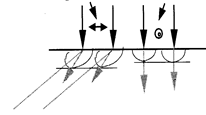Поляризация бағыттары

7.7-сурет. Кәдімгі және ерекше сәулелердің сәулелік беттерінің қималары.

Сол жақтағы көрсетілген сәулелер ерекше (немесе өзгеше) болып табылады. Ерекше сәулелер үшін, сәулелік беттерінің қималары эллипс болады. Жарықтың таралу бағыты осы эллипстер центрлерінен жанама нүктелеріне қарай өтеді. Сондықтан, кристалл бетіне нормаль түскен жағдайда да бұл сәулелер сынады.

7.7 Жарықтың жасанды қосарлана сынуы

Жасанды оптикалық анизотропия - сыртқы әсерлер нәтижесінде сәуленің қосарланып сыну құбылысын алудың жолдары көп. Үлкен тәжірибелік мәні бар анизотропия тәсілі - ол электр өрісі нәтижесінде анизотропия алу, зат молекулалары полярлы болса, олардың орналасуы өріс әсерінде кейбір жағдайда реттелген болады. Полярлы емес молекулалар өріс әсері нәтижесінде поляризацияланады. Поляризация бағыты жарықтың таралу жылдамдығының анизотропиясын анықтайтын оске айналады.

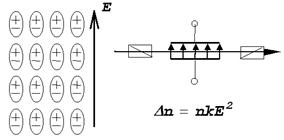
7.8-сурет. Керр ұяшығы қондырғысының сұлбасы.

Мұндай қондырғы Керр ұяшығы деп аталады (7.8-сурет). Жұмыс заты ретінде сұйық пайдаланылады. Оған параллель металл пластиналары батырылады; пластиналар жазық конденсатор құрайды, оның өрісі зат поляризациясын жасайды. Кәдімгі және кәдімгі емес сәулелердің көрсеткіштерінің айырымы Dn=n₀-n_e заттың сыну көрсеткішіне n және электр өрісінің кернеулігінің квадратына Е² пропорционал болады:

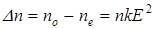, (7.20)

мұндағы k − пропорционалдық коэффициенті Керр тұрақтысы деп аталады; ол заттың температурасы мен жарық толқынының ұзындығына тәуелді. Керр ұяшығын айқышталған поляризаторлар арасына қойып, оған импульсті кернеу беретін болсақ, жүйе арқылы өтетін жарықты басқаруға болады. Жарықты қайтадан қосу уақыты өте аз шама - шамамен 10^-12 с болады.

7.8 Поляризация жазықтығының бұрылуы

Кәдімгі бұрылу. Поляризация жазықтығын бұру қабілеті бар кейбір заттар (кварц, қант, скипидар, қанттың судағы ертіндісі, шарап қышқылы) оптикалық актив заттар деп аталады. Олар арқылы өтетін жазық поляризацияланған жарық, поляризация жазықтығын бұруды туғызу қабілетіне ие болады. Кристалл заттар, жарық кристалдың оптикалық осі бойымен тараған кезде поляризация жазықтығын күшті бұрады. Тәжірибеден алынғандай, поляризация жазықтығын бұру бұрышы j оптикалық актив кристалдар мен таза сұйықтар үшін былай болады:

,

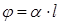оптикалық актив ертінділер үшін

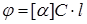, (7.21)

мұндағы l − жарықтың оптикалық актив заттағы жүрген жолы (ол заттың табиғатына, температурасына және вакуумдағы жарық толқынының ұзындығына тәуелді), С − актив заттың концентрациясы.

Поляризация жазықтығын бұру бағыты бойынша оптикалық актив заттар оңға- және солға-айналдырушы заттарға бөлінеді. Френель теориясы бойынша, шеңбер бойымен оңға және солға поляризацияланған сәулелер үшін оптикалық актив заттарда, жарықтың таралу жылдамдығы әртүрлі болады. Поляризация жазықтығын бұру құбылысы мен (7.21) формуласы оптикалық актив заттардың ертінділерінің концентрациясын дәл анықтаудың тәсілі негізінде жатыр, бұл поляриметр (сахариметр) деп аталатын тәсіл өндірісте қолданылады.

Магниттік бұрылу (Фарадей эффектісі). Оптикалық актив емес заттар магнит өрісі әсері нәтижесінде поляризация жазықтығын бұру қабілетіне ие болады. Эффект жарықтың магниттеліну бағыты бойымен таралғанда байқалады. Зерттелетін зат электромагнит полюстері арасына қойылады.

Поляризация жазықтығын бұру бұрышы j жарықтың зат ішінде жүру жолына l және заттың магниттелінуіне J тура пропорциональ болады. J= æ H болғандықтан

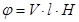, (7.22)

мұндағы V −Верде коэффициенті немесе толқын ұзындығына тәуелді меншікті магниттік бұрылу. Бұру бағыты магнит өрісі бағытымен анықталады.

Оптикалық актив заттар магнит өрісі әсері нәтижесінде кәдімгі қабілеттілікке қоса поляризация жазықтығын қосымша бұру қабілетіне де ие болады.

Нег. 2[428-443, 453-465], 7[377-398], 8[347-367].

Қос. 48[326-328].

Бақылау сұрақтары:

1. Жарықтың заттарда таралуы.

2. Қалыпты (нормаль) дисперсияның классикалық өрнегі.

3. Дисперсияның электрондық теориясы.

4. Қалыпсыз (аномаль) дисперсияның табиғаты.

5. Жарықтың жұтылуы.

6. Поляризацияланған жарықты алудың сізге қандай әдістері белгілі?

7. Жұтылатын ортада таралатын жазық сызықты поляризацияланған монохромат толқын теңдеуі қандай түрде берілген?

8. Көрінетін жарықтың затпен әсерлесуі кезінде неліктен тек электрон ғана қатысады?

8-дәріс

Жылулық сәуле шығару

8.1 Абсолют қара дененің (АҚД) сәуле шығару мәселелері.

Кванттық гипотеза және Планк өрнегі

Едәуір жоғары температураға дейінгі қыздырылған денелердің жарық шығара бастайтындығы практикада әрбір адамға белгілі. Мысалы, металдарды қыздырған кезде олар алғашқыда қоңыр қызыл түсті, артынан әрі қыздырудың барысында ашық қызыл түске ие болады, одан әрі қыздырғанда ақ шоқ деп аталатын түске келеді. Басқаша айтқанда қатты және сұйық денелер жоғары температураға дейін қыздыру кезінде спектрдің көрінетін аймағында сәуле шығаруға ие болады. Бұл кезде температураны өсіруге байланысты сәулеленудің интенсивтігі және спектрлік құрамы өзгереді. Сәулеленуші дененің ішкі энергиясы есебінен пайда болатын және тек дененің температурасы мен химиялық қасиеттеріне байланысты электромагниттік сәуле шығару жылулық сәуле шығару деп аталады. Температуралық тепе-теңдікте тұрған денелердің жылулық сәуле шығаруы денеге түсетін сәуленің энергия мөлшерін жұтуымен теңестіріледі.

Дененің жылулық сәуле шығаруының спектрлік сипаттамасы үшін дененің сәуле шығару қабілеті деген түсінік енгізіледі, оны сонымен қатар, шығарғыштық қабілеттігі немесе энергетикалық жарқыраудың Е(ν,Т) спектрлік тығыздығы деп атайды.

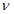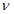Денелердің сәуле шығару қабілеті деп уақыт бірлігі ішінде дене бетінің аудан бірлігіне келетін жиіліктері -ден +d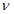аралығында шығарылатын электромагниттік сәуле шығарудың dW_сәу энергиясын айтады. Сонымен,

Е(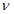,Т) = dW_сәу/ d 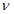(8.1)

ХБЖ жүйесінде сәуле шығарғыштық қабілетінің өлшем бірлігі ретінде [Дж/м²] алынған.

Электромагниттік толқындар жұтылуының спектрлік сипаттамасы үшін денелердің жұту қабілеті А(ν,Т) деген ұғым енгізіледі. Жұту қабілеті, уақыт бірлігі ішінде дене бетінің аудан бірлігіне жиіліктері ν-ден ν+dν аралығында түсетін dW энергиясының қандай бөлігін дене жұта алатындығын көрсетеді, яғни

А(ν,Т) = dW_жұт/dW. (8.2)

Денелердің сәуле шығару және сәуле жұту қабілеті, дененің температурасына, жиілігіне, дененің химиялық құрамына және дене бетінің күйіне байланысты болады. Егер кез-келген температурада және барлық жиіліктер үшін А(ν,Т)=1 болса, онда дене абсолют қара дене (АҚД) деп аталады. Абсолют қара дененің сәуле шығару қабілетін ε(ν,Т) деп белгілейміз. Ол дененің сәуле шығару жиілігіне және абсолют температурасына тәуелді. Абсолют қара дене әдетте физикалық үлгі ретінде алынады, бірақ табиғатта көптеген денелер өзінің қасиеттері бойынша абсолют қара денелерге жақын келеді. Мысалы қара құрым, қара елтірі, қара бархыт. Абсолют қара дененің идеалды үлгісі ретінде мөлдір емес қуыс бетіндегі кішкене тесікті алуға болады (8.1-сурет)

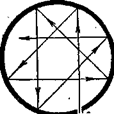
8.1-сурет. Абсолют қара дененің идеалды үлгісі.

Кішкене тесік арқылы қуыс ішіне түсетін жарық сәулесі қуыс қабырғаларына көп ретті шағылуға кездеседі. Әрбір шағылу кезінде жарық толқыны энергиясының кейбір бөлігі жұтылатын болады. Сондықтан, тесіктен шығатын сәуленің интенсивтігі, оған келіп түскен сәуле энергиясына қарағанда көп шамаға азаяды. Қуыс бетінің ауданының тесік бетінің ауданына қатынасы үлкен болған сайын, тесік беті өзінің қасиеті бойынша абсолют қара денеге соншама жақын келеді. Реал денелердің сипаттамасы үшін көп жағдайда сұр дененің үлгісі пайдаланылады. Егер дененің жұту қабілеті барлық жиіліктер үшін бірдей болып, және ол тек температура мен дене бетінің күйіне тәуелді болса, яғни А_сұр(ν,Т) = А(Т), онда дене сұр (сұр дене)деп аталады. Денелердің сәуле шығару және жұту қабілеттері бір-бірімен байланысты. Бұл байланыстарды тағайындау үшін, екі шексіз ұзын а және в пластинкалардан құралған (8.2-сурет) жылу өткізбейтін (адиабаттық)

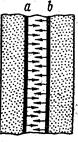8.2-сурет. Екі пластинканың жылу алмасуы.

жүйені қарастырамыз, тек пластинкалар ғана бір-бірімен жылу алмаса алады. Пластинканың а беті абсолют қара. Термодинамикалық тепе-тендік күйінде екі пластинканың температурасы да бірдей және сәуле шығару тепе-тендік күйде болады. Дененің сәуле шығару және жұту анықтамасы бойынша екі пластинка үшін былай жазуға болады:

dW_шығ= E(ν,Т) dν,

dW_жұт= А(ν,Т) dW. (8.3)

Термодинамикалық тепе-теңдік күйінде

dW= dW_шығ.

Абсолют қара а пластинкасы үшін

dW_шығ= ε(ν,Т) dν, (8.4)

а пластинкасы энергияны шағылдырмай толық жұтатындықтан, бұл пластинканың сәуле шығару энергиясы пластинкаға келіп түскен энергияға тең болады: dW_шығ=dW. Сондықтан (8.3) өрнегінен алатынымыз:

dW_жұт= А(ν,Т) ε(ν,Т) dν.

Термодинамикалық тепе-теңдік күйінде dW_шығ =dW_жұт, олай болса

E(ν,Т) dν= А(ν,Т) ε(ν,Т) dν

немесе

E(ν,Т)/ А(ν,Т)= ε(ν,Т). (8.5)

Сонымен, дененің сәуле шығару қабілетінің оның жұту қабілетіне қатынасы дененің химиялық құрамына тәуелді болмайды және ол абсолют қара дененің сәуле шығару қабілеті болып, ол температура мен жиіліктің f(ν,Т) функциясы болып табылады. Бұл заңды бірінші рет Кирхгоф тағайындады, сондықтан бұл заң Кирхгоф заңы деп аталып, ал ε(ν,Т) функциясы Кирхгоф функциясы деген атқа ие болды. Кирхгоф заңынан A(ν,Т)=1 болса, онда Е(ν,Т)=ε(ν,Т), ал егер А(ν,Т)=0 болса, онда ε(ν,Т)=∞ болады. Сондықтан, егер дене берілген температурада берілген жиіліктер аралығында жұтпайтын болса, онда ол бұл температура да және бұл жиіліктер аралығында да сәуле шығармайды, яғни сәулеленбейді.

0-ден 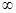-ке дейінгі жиіліктегі барлық спектр бойынша толық сәуле шығару қуаты дененің энергетикалық жарқырауы немесе интегралды сәуле шығару қабілеті Е(Т) деп аталады. Анықтама бойынша, ол мынаған тең:

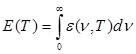
немесе Кирхгоф заңын есепке алсақ, онда

. (8.6)

Абсолют қара дене үшін A(ν,Т) = 1, сондықтан

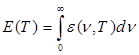. (8.7)

Бұдан әрі жылулық сәуле шығару теориясының негізгі мәселесі Кирхгоф функциясының ашық түрін іздеу болып табылады. 1879 жылы Д.Стефан тәжірибелік мәліметтерді талдау негізінде төмендегідей қорытындыға келді: кез-келген дененің энергетикалық жарқырауы абсолют температураның төрт дәрежесіне пропорционал болады. Бірақ Л.Больцман 1884 жылы термодинамикалық әдіспен теориялық түрде бұл пікірдің тек абсолют қара дене үшін дұрыс болатындығын көрсетті. Сондықтан, бұл тәуелділік физика тарихында Стефан-Больцман заңы деп аталады:

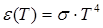(8.8)

яғни, абсолют қара дененің энергетикалық жарқырауы абсолют температураның төртінші дәрежесіне тура пропорционал.

σ=5,67∙10^-8(Вт/м²К⁴) − пропорционалдық коэффициенті Стефан-Больцман тұрақтысы деп аталады. Бірақ, олар Кирхгоф функциясының ашық түрін шешкен жоқ. Кирхгоф функциясының ашық түрін ашудағы алғашқы қадамды 1893 жылы В. Вин жасады. Ол, жылжып айналатын поршені бар және айналы қабырғалары бар цилиндрлік ыдыста абсолют қара дененің адиабатты сығу сәулеленуі туралы есепті қарастырды. Осының нәтижесінде ол Кирхгоф функциясы үшін келесі өрнекті алды:

ε(ν,Т)=f(ν,Т)=V³f(ν,Т), (8.9)

мұндағы 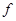(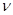,Т) − кейбір белгісіз ашық түрдегі функция. В.Вин 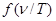функциясының ашық түрін тағайындамаса да, осы В.Виннің өрнегінен (8.9) Стефан-Больцман заңы шығады.

Абсолют қара дененің сәуле шығару қабілетінің әртүрлі температурадағы жиілікке тәуелділігі 8.3-суретте көрсетілген түрде болатындығы тәжірибелерден белгілі.

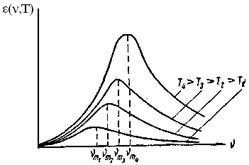
8.3- сурет. Сәуле шығару қабілетінің ε(ν,Т) жиілікке ν тәуелділігі.

Суреттен, температураның артуына байланысты абсолют қара дененің сәуле шығару қабілетінің артатындығын көреміз. Сонымен бірге қара дененің сәуле шығару қабілетінің максимум мәні, температураның өсуіне байланысты жоғары жиілік аймағына қарай орын ауыстырады. В.Вин өрнегі бұл құбылыстарды Вин заңы түрінде анықтауға мүмкіндік береді. Абсолют қара дененің сәуле шығару қабілетінің максимум мәніне келетін берілген температура кезіндегі 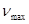сәуле шығару жиілігі Кирхгоф функциясынан алынған дербес туындыны нөлге теңестіру шарты арқылы оңай түрде анықталады:

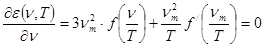. (8.10)

Соңғы тендіктен мынау алынады

.

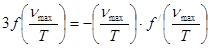Қорытындысында Виннің ығысу заңын аламыз:

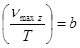. (8.11)

Заңның тұжырымы:

абсолют қара дененің сәуле шығару қабілетінің максимум мәніне келетін жиілік оның абсолют температурасына тура пропорционал болады. b − Виннің 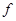(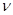/Т) функциясының ашық түрінен тәуелді болатын тұрақты шама. Әдетте Виннің ығысу заңын сәуле шығарудың толқын ұзындығы арқылы жазады:

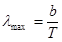, (8.12) мұндағы 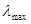− абсолют қара дененің сәуле шығару қабілетінің максимум мәніне келетін толқын ұзындығы, ол температураның өсуіне байланысты қысқа толқын ұзындығына қарай ығысады. b − Вин тұрақтысы (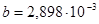мК) деп аталады, ол тәжірибелік жолмен анықталады.

Вин өрнегінен (8.9) және Виннің ығысу заңынан (8.11) абсолют қара дененің сәуле шығару қабілетінің максимум мәні абсолют температураның бес дәрежесіне тура пропорционал болады:

ε(ν,Т) = C·T⁵. (8.13)

Соңғы пікір Виннің екінші заңы деген атты қабылдайды, мұндағы С=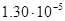Вт/м³ К⁵ − Виннің екінші заңының тұрақтысы. Кирхгоф функциясы үшін табылған алғашқы мәліметтері Д.Рэлей және Д.Джинс еңбектерінде берілген. Бұл еңбектер Максвелл көзқарастарына және статистикалық физиканың дәрістеріне негізделген. Максвелл теңдеулері бойынша тұйық қуыстағы қара сәуле шығару энергетикалық көзқарас тұрғысынан бір-бірімен әсерлеспейтін гармониялық осцилляторлардың шексіз үлкен сандарынан тұратын жүйеге эквивалентті болады. Осцилляторлардың меншікті тербеліс жиіліктері абсолют қара дененің сәуле шығару компоненттерінің сәйкес жиіліктеріне тең. Меншікті жиілігі 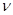, жүйе температурасы Т кезіндегі уақыт бойынша осциллятордың орташа энергиясының мәнін <_ν> арқылы белгілей отырып, Кирхгоф функциясын мына түрде беруге болады:

ε(ν,Т) = (2πν²/c²) < ε_ν>. (8.14)

Гармон

Дата добавления: 2014-01-20