Комптон эффекті

Жарықтың кванттық қасиеттері 1923 жылы А. Комптон байқаған құбылыста да білінеді. Комптон эффектісі деп рентген сәулелерінің (рентгендік кванттар) металл атомдарынан шашырауы нәтижесінде, оның толқын ұзындығының өзгеруін айтады. Спектрдің көрінетін аймағындағы жарық толқыны үшін, фотоэлектрон энергиясынан рентгендік квант энергиясы көп артық болады. Металдағы электронның байланыс энергиясы рентгенттік квант үшін аздаған кедергі болып табылады, ол электронды еркін деп есептеуге мүмкіндік береді.

Ренгендік сәулелердің ыдырауы бойынша Комптон тәжірибесінің сұлбасы 8.8-суретте көрсетілген.

8.8-сурет. Комптон тәжірибесінің сұлбасы.

Монохроматты рентгендік сәулелердің жіңішке шоғы шашырататын К затына түседі және θ бұрышына шашыраған сәулелердің толқын ұзындығын өлшейтін Д рентгендік спектрографқа енеді. Шашыраған сәулелердің 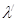толқын ұзындығы, түсетін сәулелердің толқын ұзындығынан 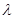едәуір үлкен болатынын, сонымен бірге айырымы тек θ шашырау бұрышына тәуелді екенін комптон тәжірибелері көрсетті:

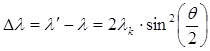, (8.23)

мұндағы 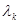тұрақтысы − Комптон толқын ұзындығы деп аталады.

Сәулелердің кванттық теориясы, Комптон құбылысын, импульстың және энергияның сақталу заңдарын сақтай отырып, рентгендік кванттардың электрондармен өзара әсерлесу нәтижесі ретінде түсіндіруге мүмкіндік берді. Импульсы р=һν/с тең атқылаушы фотон тыныштықтағы электронмен соқтығысады, нәтижесінде электрон -ға тең импульсқа ие болады, ал фотон импульсы 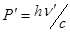-ға тең болады.

8.9-сурет. Рентген сәулесінің (фотонының) электронмен соқтығысы.

8.9-суреттен косинустар теоремасын пайдалана отырып, энергияның сақталу заңын мына түрде жазуға болады:

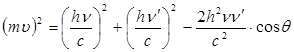. (8.24)

Рентгендік фотонның шашырауы үшін энергияның сақталу заңын келесі түрде беруге болады:

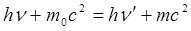, (8.25)

мұндағы 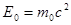− электронның тыныштық энергиясы.

(8.25) тендеуден электронның шашырағаннан кейінгі энергиясын аламыз:

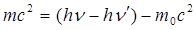. (8.26) Соңғы теңдеудің сол және оң жағын квадраттаймыз:

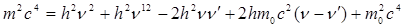. (8.27)

(8.24) тендеудің екі жағын с² -қа көбейтеміз:

. (8.28)

(8.27) теңдеуден (8.28) теңдеуді мүшелеп аламыз:

, (8.29)

екендігін ескеріп

түрлендіру жүргіземіз:

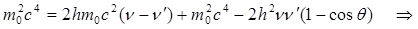
жиіліктен νтолқын ұзындығына λ көше отырып, ақырында мынаны аламыз:

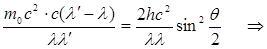
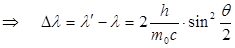. (8.30)

Теориялық түрде алынған соңғы теңдеуді (8.23) Комптон теңдеуімен салыстыра отырып,

,

Планк тұрақтысының һ, электрон массасының m₀ және жарық жылдамдығының с сандық мәндерін қойып, комптон толқын ұзындығының (λ_к) мәнін табамыз: .

Нег. 3[32-61], 7[410-419], 8 [376-381, 387-393].

Қос. 48[344-350].

Бақылау сұрақтары:

1. Қандай денені абсолют қара дене деп айтамыз?

2. Жылулық сәуле шығару заңдарын атаңыз.

3. Жиілікті арттыру кезінде Релей-Джинс заңы Вин заңына ауысуы мүмкін бе?

4. Планк өрнегін түсіндіріңіз.

5. Жарықтың кванттық қасиеттері неге негізделген?

6. Толқындық оптикадағы сыртқы фотоэффект заңдарын түсіндірудің мүмкін еместігі неден құралған?

9-дәріс

Кванттық теорияның басты идеяларын тәжірибе жүзінде негіздеу

9.1 Атомдардың сызықтық спектрлері. Бор постулаттары.

Франк және Герц тәжірибелері. Сәйкестік принципі.

Классикалық физика заңдарына құрылған планетаарлық жүйе болып табылатын және a бөлшектерінің шашырауы бойынша жүргізілген тәжірибелердің нәтижелерін талдауға негізделген Резерфордтың атомдық моделі тәжірбиелік фактілермен толық қарама-қарсы қайшылықта болды. Біріншіден, классикалық теорияға сәйкес, электрон ядроның айналасында дөңгелектік орбита бойынша қозғала отырып, үздіксіз сәуле шығаруға тиіс. Шындығында, атом тек кейбір шарттар негізінде ғана сәуле шығарады. Екіншіден, Резерфордтың атомдық моделі тұрақсыз болды, бірақ шындығында атом тұрақты жүйе болып табылады. Үшіншіден, Резерфорд моделіндегі атомның сәуле шығару спектрі үздіксіз (тұтас) болуы керек еді, ал бірақ тәжірибеде атомның сәуле шығаруы сызықтық спектр болып табылады. Бұл деген сөз, классикалық физика заңдарын атом теориясына біркелкі қолдану тәжірибелік фактілермен қарама-қарсы қайшылықта болуға әкелді.

Алдымен, атомдардың сәуле шығаруының кейбір заңдылықтарын қарастырайық. Жарқырауық газдар сәулеленудің сызықтық спектрлерін беретіндігі белгілі. 1885 жылы И. Бальмер сутегі атомы спектрінің көрінетін бөлігінің тоғыз сызығының толқындық ұзындығын

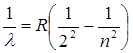, (9.1)

өрнегімен анықтауға мүмкін болатынын тағайындады. Мұндағы Ридберг тұрақтысы деп аталады, ал n=3,4,5,…

Бальмер өрнегін (9.1) сәуле шығару жиілігі үшін мына түрде жазуға болады:

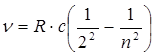, (n=3,4,5...). (9.2)

Мұнда толқын ұзындығы мен жиілік арасындағы байланысты қатысты пайдалануға болады, с =3×10⁸ м/с – вакуумдағы жарық жылдамдығы. Р. Ридберг сутегі атомы үшін ғана емес, сонымен бірге басқа элементтерде сызықтық спектрлер байқалатынын көрсетті, спектрлік сызықтардың жиілігі

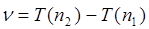, (9.3)

қатынасын қанағаттандырады, мұндағы n₁ және n₂ – кейбір бүтін сандар. Т(n₁) және Т(n₂) функциялары спектрлік термдер деп аталады. (9.2) және (9.3) өрнектерін салыстыра келіп

;

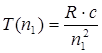болатындығы шығады. 1908 жылы В. Ритц, кез-келген атомның сәулеленуінің спектрлік сызықтарының жиілігі екі терм айырымы түрінде беруге болатындығын тағайындады; термдердің әртүрлі комбинацияларын құрай отырып, бұл атомның спектрлік сызықтарының мүмкін болатын барлық жиілігін табуға болады. Мұндай ұйғарым Ритцтің комбинациялық принципі деген атқа ие болды. Ритцтің комбинациялық принципін қолданып, сутегі атомының сәулелену сызықтарының толқын ұзындығын есептеуге мүмкін болатын сериалды өрнектерді алуға болады.

Спектрдің алыс ультракүлгін аймағында бақыланатын Лайман сериясы мынадай өрнек арқылы сипатталады:

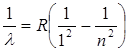, (9.4)

мұндағы n=2,3,4,…

Сутегі атомы спектрінің көрінетін аймағында бақыланатын Бальмер сериясы келесі өрнекпен сипатталады:

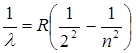, (9.5)

мұндағы n=3,4,5,…

Спектрдің инфрақызыл аймағында бақыланатын Пашен сериясы мына өрнек бойынша сипатталады:

, (9.6)

мұндағы n=4,5,6,…

Сонымен бірге, алыс инфрақызыл аймағында келесі сериялар байқалған:

Брэкет сериясы

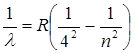, (9.7)

мұндағы n=5,6,7,…

Пфунд сериясы

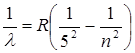, (9.8)

мұндағы n=6,7,8,…

Хэмфри сериясы

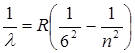, (9.9)

мұндағы n=7,8,9,…

Атомның классикалық емес теориясын құрудың алғашқы талпынысын 1913 жылы дат физигі Н. Бор жасаған. Бірақ Бордың теориясында Резерфорд моделінің көзқарасынан алшақ кетпеушілік байқалады. Атомдағы электронның күйіне арнайы шектеулер енгізді. Атом моделі Бор тағайындаған постулаттарға құрылды.

Бордың бірінші постулаты: атом, кейбір стационар күйлерде өзінен электромагниттік толқын (жарық) энергиясын шығармайды және жұтпайды.

Бордың екінші постулаты: бір стационар күйден екінші стационар күйге көшкенде атом бір квант энергиясын шығарады немесе жұтады. Бұл постулат жиіліктер ережесі болып табылады және оны келесі түрде өрнектеуге болады: атом бір стационар күйден екінші стационар күйге көшкенде, стационар күйлердің энергиялар айырымына тең болатын һn квант энергиясын шығарады немесе жұтады, яғни

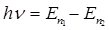(9.10)

Импульс моментінің квантталуы: атомның стационар күйіндегі электрон, импульс моменті Планк тұрақтысына еселік болатын дөңгелектік орбита бойынша қозғалады, яғни мына шартты қанағаттандырады:

, (9.20)

мұндағы m – электрон массасы, – электрон жылдамдығы, r – электрон орбитасының радиусы, , n=1,2,3,… – сутегі атомының энергетикалық деңгейлерінің ретін анықтайтын бүтін сандар, олар бас кванттық сандар деп аталады.

Кейде (9.20) өрнекті Бордың үшінші постулаты деп те атайды. Дегенмен, импульс моментінің квантталуы Бордың 1-ші постулатының салдары болып табылады. n=1 сәйкес мәніне тең күй – негізгі күй деп аталады, ал n>1 барлық басқа күйлер қозған күйлер деп аталады. Бор постулаттары сутегі атомының стационар күйлерінің энергияларын және орбиталарының радиустарын анықтауға мүмкіндік береді. Енді, атомның стационар күйлерінің (n-ші орбитасының) толық энергиясын және n-ші орбитасының радиусын анықтайық. Бұл кезде Бордың есептеуі бойынша, сутегі атомындағы электрон, электронның ядроға кулондық тартылыс күш әсерінен классикалық заң бойынша дөңгелек орбита бойымен қозғалады. Сутегі атомындағы электрон үшін Ньютонның екінші заңын жазып, мынаны аламыз:

. (9.21)

Соңғы өрнектен электрон орбитасының r радиусын анықтаймыз

. (9.22)

Электрон орбитасының радиусы үшін (9.22) өрнегін (9.20) өрнегіне қойып, түрлендіруден кейін n-ші орбитасындағы электронның жылдамдығын табуға болады

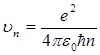. (9.23)

(9.22) пен (9.23)-тен сутегі атомындағы электронның n-ші орбитасының радиусы:

. (9.24)

Соңғы теңдеуден, орбита радиусы бүтін сан квадратына n² пропорционал түрде өсетіндігі көрінеді. Сутегі атомындағы электронның толық энергиясы оның кинетикалық және потенциялық энергияларының қосындысынан тұрады. Электронның кинетикалық энергиясы мына өрнек бойынша анықталады:

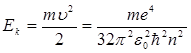. (9.25)

Сутегі атомындағы электронның потенциялық энергиясы мынаған тең:

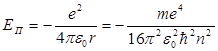. (9.26)

Сутегі атомындағы электронның толық энергиясы:

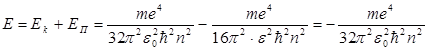. (9.27)

Сонымен, сутегі атомы туралы Бор көзқарасы атомның мөлшерін дәл анықтауға мүмкіндік берді. n=1 кезінде

. (9.28)

Бұл шаманы сутегі атомының бірінші радиусы (немесе Бор радиусы) деп атайды. Сутегі атомындағы электронның толық энергиясы теріс шама болғандықтан, ол бас

9.1-сурет. Сутегі атомының шығару спектрі.

кванттық санның (n) өсуіне байланысты артады және n®¥ кезінде, Е=0 болады. Сутегі атомының спектрлік сәуле шығару сызықтарының пайда болуы 9.1 - суретте көрнекті түрде талқылануы алынған.

Атомдардағы стационарлық күйлердің (дискретті энергетикалық деңгейлердің) пайда болуы туралы Бор постулаттары және жиіліктердің ережесі 1913 жылы Д.Франк пен Г.Герцтің тәжірибелерінде өзінің орнын тапты. Тәжірибелік қондырғының сұлбасы 9.2-суретте көрсетілген.

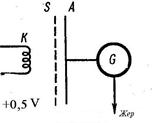
9.2-сурет. Франк-Герц тәжірибесінің сұлбасы.

Өте қатты қызған спираль түріндегі К катоды электрондарды шығарады, электрондар электр өрісінің әсерінен гальванометрге жалғанған А анодқа қарай қозғалады. Катод пен анодтың арасында S тор электроды бар. Бұл барлық жүйе ішінен ауасы сорылып алынған шыны баллонына орналастырылады. Баллонда, шамамен 15 Па дейінгі қысымда сынап булары енгізілген. Катод пен тор арасында потенциалдар айырымы U₁ болатын үдеткіш электр өрісі жасалған, ал тор мен анод арасында потенциалдар айырымы U₂ болатын шамасы 0,5 В-тан аспайтын әлсіз тежеуші кернеу өрісі жасалған. Электрондар сынап атомдарымен екі жақты әсерлеседі. Соқтығысудың бірінші түрі серпімді соққылар, олар электрондардың жылдамдығын өзгерусіз қарапайым шашырауға әкеледі. Мұндай серпімді соққылар тізбектегі толық токтың болмауының себебі бола алмайды, ол үдеткіш U₁ потенциалдар айырымы артуына байланысты өседі. Соққының екінші түрі – электрондардың сынап атомдарымен серпімсіз соққысы – электрондардың энергия жоғалтуына байланысты және ол бұл энергияларды сынап атомдарына беруіне байланысты. Бірақ, Бор постулаттарына сәйкес, сынап атомы кез-келген энергияны қабылдамауы мүмкін, ол тек әртүрлі энергетикалық деңгейлердегі энергиялар айырымына тең энергияның белгілі үлесін ғана қабылдайды. Сынап атомының негізгі күйіне жақын күй - қозған күй болып табылады, ол негізгі күйден 4,86 эВ энергия айырымына өзгереді.

Осымен байланысты өрістің үдететін электрондары энергия айырымы еU₁=4,86 эВ-қа дейін жеткенше тек серпімді соққыларға ие болады. Электрондар энергиясы 4,86 эВ жетісімен серпімсіз соққылар басталады, бұл кезде электрон толық энергияны сынап атомына береді. Сынап атомымен соқтығысу нәтижесінде өзінің энергиясын жоғалтқан электрон тор мен анод арасындағы тежеуші өрісті жеңе алмай, нәтижесінде электрон анодқа жете алмайды. Бұл анод тогының кенет тез түсуіне әкеледі (9.3-сурет).

9.3-сурет. Анодтық токтың I кернеуге U тәуелділігі.

Осындай құбылыс еU₁=2×4,86 эВ кезінде де болады, жалпы айтқанда еU₁=n×4,86 эВ кезінде де болатындығын Бор постулаттары дәлелдейді.

Бор теориясы атомдық физикасының дамуы барысында өте зор орын алады. Ол сутегі атомы энергиясының сәулеленуі мен жұтылуының сызықтық спектрлерін түсіндіруге, теориялық түрде сутегі типтес жүйелер үшін Ридберг тұрақтысын есептеуге, атомның тұрақтылығын, рентгенттік сәулеленудің табиғатын және тағы басқа құбылыстарды түсіндіруге мүмкіндік берді. Бірақ Бор атомының моделі атомдағы электрондардың қозғалысы туралы жартылай классикалық көзқарасқа байланысты өз ішінде қайшылықтар болды. Бор теориясы ядродан басқа екі электроннан құралған гелий атомының моделін жасай алмады. Сонымен бірге, Бор теориясы спектралды сызықтардың интенсивтігіндегі әртүрлілікті түсіндіре алмады. Оларды есептеу үшін Бор тағайындаған сәйкестік принципін қолдануға тура келді. Бұл принцип бойынша кванттық механиканың нәтижелері үлкен кванттық сандар кезіндегі классикалық нәтижелерге сәйкес болуы керек. Бұл принцип, классикалық теорияның дамуы болып табылатын кез-келген теория мен алғашқы классикалық теория арасында заңды байланыс болатынын, яғни жаңа теория ескі теорияға шекті жағдайларда ауысатындығын көрсетеді.

10-дәріс

10.1 Жарықтың корпускулалы-толқындық екіжақтылығы. Де-Бройль болжамы. Электрондардың дифракциясы (Дэвиссон-Джермер тәжірибесі). Микробөлшектердің толқындық қасиеттері және Гейзенбергтің анықталмағандық қатынасы. Толқындық функция және оның статистикалық мағыынасы.

Жарықтың бір мезгілде үздіксіз шексіз таралатын толқындық және бөлшектік (фотондар) қасиетке ие болатындығын айтқан болатынбыз, яғни жарықтың дискреттік (үзік-үзік құрылымының) қасиетінің толқындық қасиетке қарама-қарсы екендігін айтқан болатынбыз. Бұл жарық толқынының екіжақтылығын, яғни корпускулалы – толқындық қасиетінің бар екендігі жөнінде әңгіме жасауға болады. Жарықтың мұндай қарама-қарсы қасиетінің пайда болуы белгілі бір заңдылыққа бағынады, яғни толқын ұзындығы қысқарған сайын (немесе жиілігі көбейген сайын) жарықтың кванттық қасиетінің бар екендігі айқындала түседі. Осыған байланысты корпускулалы – толқындық туралы екіжақты тек жарық толқындары үшін ғана емес, кез-келген толқындық процесс үшін де айту керек. Егер, фотонды толқындық қасиеті бар бөлшек деп қарау керек болса, онда бұл есептегі микроскопиялық болатын бөлшектің толқындық қасиетін жоққа шығарудың себебі жоқ болады.

1924 жылы Француз физигі Луи де-Бройль корпускулалы-толқындық табиғаты бар сипаттамаларды тек электромагниттік толқындар үшін ғана емес, кез-келген дененің қозғалыстағы бөлшектерінің барлығына қолдану керек деген қорытындыға келді. Фотонның импульсі үшін жазылған өрнекті де-Бройль кез-келген толқындық процестерге қолдануға болатындығын дәлелдеді, егер қозғалыстағы дене бөлшегінің импульсі болса, онда:

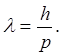(10.1)

Бұл (10.1) өрнегі де-Бройль формуласы деп аталады және ол қазіргі заманымыздың физикасының өте қажетті формуласы болып саналады. Массасы 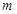, қозғалу жылдамдығы <<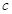бөлшектер үшін:

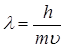. (10.2)

Егер, бөлшектің кинетикалық энергиясы Е болса, онда энергиясын және импульсын еске алып мынадай формула жазуға болады

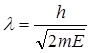. (10.3)

Айта кету керек, де-Бройль толқыны электрмагниттік емес. Олардың табиғаты ерекше, себебі классикалық физикада оларды салыстыратын теңеу жоқ. Де Бройль толқыны барлық қозғалыстағы бөлшектерді сипаттайтын әмбебап болып саналады. Мысалы, массасы 0,01 кг, жылдамдығы 1000 м/с оқ үшін де-Бройль толқынының ұзындығы мынадай болады:

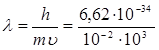(м)=0,662 ∙ 10^-34м.

Дифракциялық тәжірибенің нәтижесі бойынша, ядроның өлшемі 10^{-15 м -дей болса, 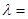10-34 м толқын ұзындығын көру мүмкін емес екендігі белгілі. Ал микроскопиялық денелерге өтетін болсақ, мәселе басқаша. Мысалы, жылдамдығы 106} м/с және массасы m_э=9,1∙10^-31кг электрон үшін де-Бройль толқын ұзындығы м шамасында болады.

Де-Бройль болжамы 1927ж никель монокристалынан электрондардың шашырауын бақылаған К. Дэвиссон мен Л. Джермердің тәжірибелерінде

(10.1-сурет) расталды.

Электрондық зеңбірек электронды белгілі бір жылдамдықпен шығарып, никель монокристалына тиіп және одан электрондар шоғы шашырайды. Шашыраған электрондарды қабылдаушы ретінде Фарадей цилиндрі қолданылды, Фарадей цилиндріне түскен электрондар саны цилиндрдің электр тізбегіндегі ток күшіне пропорционал болған. Классикалық физика тұрғысынан электрондар мүмкін болатын бұрыштармен шашырауы керек. Бірақ та электрондардың 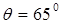-тан кіші бұрыштармен шашырауын бақылағанда, электр тізбегіндегі шашыраған электрондардың максимум саны (ток күшінің максимумы), энергиясы 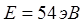электронға (10.2-сурет) тура келді, ол 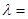0,167 нм де-Бройль толқын ұзындығына сәйкес келеді. Электрондардың шашырауы.

Брэгга-Вульф шарты орындалған кездегі рентген сәулелерінің шашырауына ұқсас:

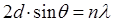. (10.4)

Сонымен, Дэвиссон мен Джермер тәжірибелері де-Бройльдың электрондарының толқындық қасиеті бар гипотезасын дәлелдеді. Кейінірек электрондардың толқындық қасиеті басқа да тәуелсіз тәжірибелермен дәлелденді. Де Бройль толқындарының кейбір қасиеттерін қарастырайық. Де Бройль толқынының фазалық жылдамдығын есептейік. Кез- келген толқынның фазалық жылдамдығы мынаған тең:

, (10.5)

мұндағы – толқындық вектор, оның модулі 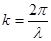-ға тең. Түрлендіруден кейін

, (10.6)

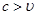болғандықтан, де-Бройль толқынының фазалық жылдамдығы вакуумдағы жарық жылдамдығынан артық болуы мүмкін. Де-Бройль толқынының топтық жылдамдығын мына формула бойынша есептейміз

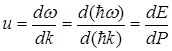. (10.7)

Еркін бөлшектер үшін 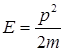, олай болса

(10.8)

Соңғы өрнектен, де-Бройль толқынының топтық жылдамдығы бөлшектің өзінің жылдамдығына тең. Бұл де Бройль толқындары ерекше табиғатқа ие және оларды кеңістікте уақыт бойынша жайылатын толқындық пакет ретінде қарастыруға болмайтынына қажетті дәлелдеме болды. Топтық жылдамдық үшін өрнекті түрлендірейік

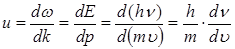. (10.9)

Де-Бройль толқынының топтық жылдамдығы бөлшектің өзінің жылдамдығына тең екенін ескерсек, онда:

. (10.10)

Соңғы өрнекті интегралдап, мынаны аламыз:

. (10.11)

Соңғы теңдеу де-Бройль толқынына сәйкес келетін жиілік пен еркін бөлшектің энергиясының байланысын өрнектейді. Кристалдардағы электрондардың шашырауы бойынша жүргізілген тәжірбиелерде, жоғарыда көрсетілгендей басқа барлық бағыттарға қарағанда жеке бағыттарды электрондардың үлкен санының шашырайтындығы байқалады. Толқындық көзқарасынан қарағанда, кейбір бағыттарда электрондардың максимум санының болуы, бұл бағыттарда де-Бройль толқынының үлкен интенсивтігі бар екенін білдіреді. Толқын интенсивтігі тоқын амплитудасының квадратына 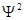пропорционал болатындығын есепке ала отырып, де-Бройль толқынына өздігінше ықтималды талқылама беруге болады. Кеңістіктің берілген көлеміндегі де-Бройль толқынының амплитуда модулының квадраты , бөлшектің осы көлемде бар болу (немесе табылу) ықтималдығын білдіреді.

Берілген уақыт мезетінде тұрған бөлшектің ықтималдылығы орналасуын сипаттау үшін деп аталатын толқындық функция, кеңістіктің кейбір аумақтарына координат пен уақыттың функциясы енгізіледі. 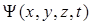толқындық функциясының жеке өз бетінше физикалық мәні болмайды, тек толқындық функция модулінің квадратының мәні болады. Оны келесі түрде анықтайық: 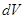көлем элементінде тұрған бөлшектің ықтималдығы толқындық функция модулінің квадратына |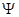|² және 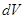көлемінің элементіне пропорционал болады, яғни

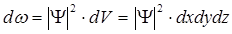. (10.12)

Ықтималдық тығыздығы

. (10.13)

Бұл өрнек кеңістіктің берілген dV көлемде бөлшектің бар болу ықтималдылығын анықтайды. Сондықтан толқындық функция модулінің квадраты, мұндағы − 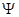толқындық функцияның комплексті түйіндес функциясы. Ол кеңістіктің берілген нүктесіндегі бөлшектің табылу ықтималдығын көрсетеді. Басқаша айтқанда шамасы де-Бройль толқынының интенсивтігін анықтайды. Анықтама бойынша толқындық функция келесі шартты қанағаттандыруы керек

, (10.14)

мұндағы үштік интеграл 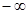тен 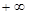ке дейінгі барлық кеңістік бойынша есептеледі. (10.14) өрнек бөлшектің шексіз кеңістіктегі қандай да бір элементар көлемде dV табылатындығын көрсетеді және оның ықтималдығы бірге тең шама болуы керек. (10.14) өрнегін толқындық функцияның нормалау шарты немесе ықтималдықты нормалау шарты деп атайды. Бөлшектер қасиеттерінің корпускулалы-толқындық екіжақтылығы және 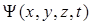толқындық функцияның ықтималдылық мәні кеңістіктегі бөлшектің күйін анықтау микродүниедегі классикалық физика заңдарының қолданымдылық шекарасы туралы мәселені талдауға бізді жетелейді. Оптика бойынша оқылатын дәрістерде монохромат толқындар алу мүмкіндігін қарастыра отырып, электромагнитті толқындардың атомдармен сәулелену сипаттамасын талқыладық.

Атомдардың сәулелену импульсін әртүрлі амплитудалары да, жиіліктері де және фазалары да әртүрлі гармониялық тербелістердің жиынтығы түрінде деп көрсетуге болады. Тәжірибеден белгілі болғандай импульста құралатын жиілік интервалының ені, атомның импульстік сәулелену ұзақтығына кері пропорционал болады, яғни

. (10.15)

Импульстік сәулелену ұзақтығының импульстік сызықтық мөлшерімен байланысы қатысы арқылы беріледі, бұдан . Сонымен бірге

ескеріп (10.15)-ті түрлендіреміз

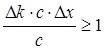. (10.16)

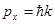-ты пайдаланып 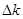-ны -ға ауыстырсақ, ; Соңында алатынымыз:

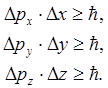(10.17)

(10.17) қатынасы Гейзенбергтің анықталмағандық қатынастары деп аталады. Гейзенбергтің анықталмағандық қатыстары кванттық механиканың құрылуында шешуші рөл атқарады.

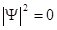
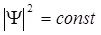Гейзенбергтің анықталмағандық қатыстарының мәнін талдайық. Толқындық функция модулінің квадраты -тан басқа барлық жерде орындалатын болсын. Егер импульс анықтамасы барысында анықталмағандық нөлге тең болса, , яғни берілген жылдамдықтағы электрон қозғалысы дәл белгілі, онда (10.17)-тен шығады. Бұл кезде және ықтималдығы бөлшек кеңістіктің кез-келген нүктесінде бола алады. Және керісінше, егер кеңістіктің белгілі нүктесінде электрон тұрса, онда 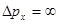, яғни оның жылдамдығы және импульсі 0-ден 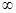-ке дейінгі кез келген мәндерді қабылдауы мүмкін. Бөлшек массасының артуымен бөлшек күйін анықтаудағы анықталмағандық және оның импульсі артады және макробөлшектердің қозғалуы кезінде бұл анықталмағандық тіптен есепке алынбауы мүмкін. Гейзенбергтің (10.17) анықталмағандық қатынастарынан

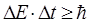. (10.18)

шығады. Гейзенбергтің анықталмағандық қатынастары атомдағы электрон қозғалысын жаңаша қарастырады. Ол бойынша белгілі траектория бойынша қозғалатын атомдағы электрон қозғалысының дәл жылдамдығы туралы айтуға болмайды. Атомдағы электрон ядроны қоршайтын шар қабатында кейбір ықтималдықпен тұруы мүмкін, бұл кезде электрон энергиясын анықтаудағы қателік ∆Е шамасына тең болады. Сонымен, микробөлшектердің қозғалысын сипаттау кезінде траектория түсінігі өзінің мәнін жоғалтады, өйткені кеңістіктегі орны белгілі ықималдықпен анықталған микробөлшектің импульсі немесе жылдамдығы тек қандай да бір қателікпен анықталуы мүмкін.

Кіші өлшемді жүйелер физикасы – нанотехнологияның іргелі негізі.

Кез-келген дененің көлемі үш өлшемді кеңістікте анықталады. Шала өткізгіштердегі электронның толқын ұзындығы шамамен 100 нм-ге тең. Сондықтан осындай масштабтарда электронның толқындық табиғаты (қасиеті) байқалады, ал бұл жағдайда электронның заряд тасымалдаушылар қозғалысын кванттық механика заңдылықтары арқылы анықтауымыз керек. Заттар ішіндегі кеңістік масштабы 1:100 нм болғандықтан, электр зарядын тасымалдаушылардың қозғалысы шектеулі болады. Көрсетілген аралықта (диапазонда) 1:100 нм бір немесе бірнеше нысандар өлшемдерін анықтау үшін кванттық-механикалық процесстер мен құбылыстар қарастырылады және олардың макроқұрылымдары мен жүйелерден ерекше айырмашылығы бар, олар өлшемдері өте кіші наноқұрылымдар класын құрайды. Соңғы 10-15 жылдар ішінде наноқұрылымдардағы физикалық құбылыстарды зерттейтін кіші өлшемдер жүйесі физикасы деп аталатын жаңа бағыт пайда болды. Кіші өлшемді жүйелер физикасы кванттық жіптер (нить) және кванттық нүктелер қасиеттерін зерттейді.

Егер заттағы электронның қозғалысы тек бір бағытпен шектелсе, мұндай нысан кванттық шұңқыр деп аталады, ал электр зарядын тасымалдаушы бөлшектер екі өлшемді деп есептеледі. Заряд қозғалысы екі бағытпен шектелсе, онда бірөлшемді кванттық жіп пайда болады, ал заряд қозғалысы үш бағытта шектелсе, өлшемсіз (ұзындық бойынша) кванттық нүкте құралады. Наноқұрылым нысандарына тиісті барлық табиғи және жасанды жүйелер осы аталған кванттық шұңқыр, жіп немесе нүктеге байланысты болады. Сондықтан кіші өлшемді жүйелер физикасы нанотехнология деп аталатын процесстер мен құбылыстардың іргелі негізін құрайды. Ресейде нанотехнология бағытында мамандар дайындауға ерекше көңіл бөлінгенін атап өтуіміз керек. Бұл бағыттағы ғылыми кеңесті кіші өлшемді жүйелер физикасына зор үлес қосқан Нобель сыйлығының иегері академик Ж.И. Алферов басқарады.

Сонымен, «нанотехнология» атом, молекула өлшемдерінде болатын материалдарды жасау және пайдалану, нанометрлік масштабтағы құрылымдар мен жүйелерді зерттейді. Нанотехнология осындай нысандармен жұмыс істеу қабілетін, олардан (атомдардан) күрделі молекулалық заттарды жасау жолдарын қарастырады. Атом-молекулалық элементтерді пайдалану арқылы жасанды түрде өте майда жаңа құрылымдарды жасау көзделеді. Бұл құрылымдар жаңа физикалық, химиялық және биологиялық қасиетттерге ие болып, жаңа құбылыстарды зерттеуге мүмкіншілік туады. Осыған байланысты бірқатар елдерде наноғылым, нанотехнология түсініктері (терминдері) пайда болды (наноғылым өте кіші масштабтардағы наноматериалға байланысты құбылыстар мен қасиеттерді терең түрде зерттейді, нанотехнология жаңа құрылымдарды жасаумен, ал наноинженерлік оларды тиімді пайдалану жолдарымен айналысады).

Соңғы жылдардағы зерттеулер ғылым мен техниканың әр түрлі салаларында наноқұрылымдарды пайдаланудың өте зор мәні бар екендігін көрсетті (физика, химия, материалтану, биология және т.б.). Мысалы, көміртекті нанотұтіктер болатқа қарағанда 9-10 есе төзімді (қаттылығы) екендігі, нанобөлшектердің рак клеткаларына кіріп оларды жоятындығы, кейбір наноқұрылымдардың электрондық есептеу машиналарының жұмыс істеу жылдамдығын миллион есе арттыратындығы және т.б. құбылыстар анықталды. Табиғи нысандар мен тірі организмдердің құрылысы және қызметі туралы біздің біліміміздің молекулалық деңгейде тереңдеуі нәтижесінде наноөлшемді құрылымдағы жасанды материалдарды жасау және пайдалану бағытында жалпы заңдылықтарды анықтауымыз қажет болды.

Шын мәнінде табиғаттағы барлық материалдар мен жүйелер нанонысандардан тұрады. Табиғат заттардың, құбылыстар мен процесстердің негізгі сипаттамаларын молекулалық деңгейде, наноөлшемдерде «бағдарламалап» қойған болып шығады. «Нанотехнологиялық әдіс нысандар қасиетін молекулалық деңгейде белгілі-бір бағыттауға, негізгі параметрлерді анықтау және реттеуге мүмкіншілік береді.

Нанометрлік масштабта заттардың қасиеттерінің ерекшелігін және онымен байланысты жаңа физикалық құбылыстар нанонысандар өлшемдерінің жай материалдар атомдары мен молекулаларымен шамалас екендігінен келіп шығады. Осы тұрғыдан наноқұрылымдарды заттардың ерекше фазалық күйі деп те қарастыруға болады. Нанометрлік аралықтағы құрылым элементтерінен пайда болған заттар мен материалдардың қасиеттері көлемдік фазада анықталмайды. Олардың сипаттамаларының өзгеруі құрылым элементтері өлшемінің кішіреюіне ғана емес, кванттық-механикалық эффекттердің әсеріне, тасымалдау процесінің толқындық табиғатына және шекаралық беттік процесстерге де тәуелді болады. Наноқұрылымдардың өлшемдері мен пішінін басқару арқылы, кәдімгі материалдар сипаттамаларына мүлде ұқсамайтын, жаңа функционалдық сипаттамалар енгізуге болады. Бұл наноқұрылымдарға қазіргі кезде белгілі көміртекті нанотүтікшелерді, белоктарды, ДНК және үй температурасында жұмыс істейтін «бірэлектрондық» транзисторды жатқызуға болады. Егер ғалымдар наноқұрылымдардың және осындай нысандардың қасиеттерін анықтайтын заңдылықтар мен принциптерін толық игерсе ғылым мен техникада өте үлкен жаңалықтар пайда болар еді.

Нанотехнология материалдар мен жүйелерге жаңа қасиеттер мен сапа беруі нәтижесінде тіршіліктің барлық саласында (компьютерлік техника, емдеу техникалық жетісітіктер және т.б.) өте үлкен жетістіктерге жетуге мүмкіншілік тудырады.

Нег. 3[62-86], 7[422-431], 8 [393-400]. 2[316-346], 8[304-316]

Қос. 48 [350-361].

Бақылау сұрақтары:

1. Жарық қасиеттерінің корпускулярлы-толқындық екіжақтылығы неден құралады?

2. Анықталмағандық қатыстарын пайдаланып, белгілі фотон импульсі бойынша оның локализация аймағын анықтауға бола ма?

3. Толқындық функцияның статистикалық мәні неде?

4. Кіші өлшемді жүйелер туралы түсінік.

5. Кванттық шұңқыр.

6. Кванттық жіп.

7. Кванттық нүкте.

8. Нанотехнологияның қолдану салалары.

11-дәріс

Шредингердің жалпы және стационар теңдеулері. Бір өлшемді потенциалдық шұңқырдағы бөлшек. Бөлшектің потенциалдық тосқауыл арқылы өтуі (Туннелдік эффект)

Кванттық механикадағы бөлшектің күйін, координат пен уақытқа тәуелді Ψ(x,y,z,t) толқындық функцияның берілуі бойынша анықталатындығын өткен дәрістерде біз түсіндірген болатынбыз. Сондықтан, кванттық механикадағы толқындық функцияның түрін іздеу үшін, классикалық механикадағы Ньютонның қозғалыс теңдеуі сияқты теңдеуді алу керек. Мұндай теңдеуді 1926 жылы Э.Шредингер тапты. Шредингер теңдеуі қорытылмайды, ол белгілі тәжірибелік фактілер негізінде постулаттандырылады және оның растығы теориялық есептер мен тәжірибелік мәліметтердің сәйкес келуімен дәлелденеді. Жалпы жағдайда Шредингер теңдеуінің түрі

, (11.1)

мұндағы m – бөлшектің массасы, 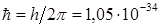Дж×с – 2p-ге бөлінген Планк тұрақтысы, – жорамал сан, Ψ(x,y,z,t) – толқындық функция, U(x,y,z,t) – күштік өрістегі бөлшектің потенциялдық энергиясы, 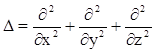– Лаплас операторы.

(11.1) теңдеуі v<<c жылдамдықпен (с – вакуумдағы жарық жылдамдығы) қозғалатын кез-келген микробөлшек үшін орынды. Шредингер теңдеуі Ψ(x,y,z,t) толқындық функциясына қосымша шарттар қояды:

1. Ψ (x,y,z,t) толқындық функциясы шекті, үздіксіз және бірмәнді болуы қажет;

2. Ψ(x,y,z,t) толқындық функциясы үздіксіз дербес туындыларға ие болуы керек;

3. Ψ(x,y,z,t) функциясы интегралдануы керек, яғни 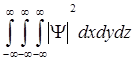интегралы шекті болуы қажет.

(11.1) Шредингер теңдеуі жалпы жағдай үшін шешілмейді. Бірақ, бұл теңдеудегі потенциялық энергия уақытқа тәуелсіз, яғни бөлшек қозғалатын күштік өріс стационарлы болатын есептер үшін қысқартуға болады. Бұл жағдайда Ψ(x,y,z,t) толқындық функцияны екі толқындық функцияның көбейтіндісі ретінде жіктейміз: y(x,y,z) – тек координатқа тәуелді және j(t) – тек уақытқа тәуелді:

. (11.2)

(11.2) өрнегін (11.1) Шредингер теңдеуіне қойып, мынаны аламыз

.

Соңғы теңдеудің оң және сол жағын y×j көбейтіндісіне бөлеміз:

. (11.3)

Теңдеудің сол жақ бөлігі тек координатқа, ал оң жақ бөлігі тек уақытқа тәуелді болғандықтан, бұл теңдіктің әр жағы жеке-жеке тұрақты бір шамаға тең болған жағдайда ғана орындалады. Ол тұрақты шама энергияның өлшемін иемденуі керек және U(x,y,z) потенциялық энергиясы бар күштік өрістегі қозғалатын бөлшектің толық энергиясы болуы керек, яғни -Е. Осыдан екі теңдеу аламыз: біріншісі тек уақытқа тәуелді

, (11.4)

екіншісі тек координатқа тәуелді (Шредингердің стационарлы теңдеуі)

,

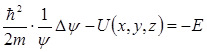мұны келесі түрде жазуға болады:

. (11.5)

Шрёдингердің стационарлық теңдеуі (11.5) кез-келген U(x,y,z) үшін шешіле бермейді, бірақ кейбір дербес жағдайларда бұл теңдеудің шешімін табуға болады. Берілген U(x,y,z) үшін Шредингер теңдеуін қанағаттандыратын толқындық функциялар меншікті функциялар деп, ал осы кездегі Шредингер теңдеуінің шешімі табылатын Е-нің мәндері энергияның меншікті мәндері деп аталады. Айнымалы шамаларды бөле отырып (11.4) теңдеуін интегралдауға болады

.

Соңғы теңдеуден (11.4) теңдеуді қанағаттандыратын толқындық функцияны аламыз

, (11.6)

мұндағы j₀ – j функциясының амплитудалық мәні.

Бір өлшемді потенциалдық шұңқырдағы электронның қозғалысы туралы есепті қарастырып көрейік. Потенциалдық шұңқыр деп 11.1-суретте көрсетілгендей түрі бар, U(x)-тың х-қа тәуелділігін айтады.

Мұндай қозғалыстың, мысалы ретінде металл ішіндегі электрондардың қозғалысын қарастыруға болады. Бұл жағдайда металл сыртындағы электрон ның потенциалдық энергиясы нөлге тең. (11.1-суреттегі І және ІІІ аймақтар – шұңқыр сырты |x|>a, U=0), ал металл ішіндегі потенциялы теріс мәнге ие және электронның металдан шығу жұмысына тең (11.1 суреттегі ІІ аймақ, шұңқыр іші, |x|<a, U=-U₀).

11.1-сурет. Бірөлшемді потенциалдық шұңқыр.

Потенциалдық шұңқырдың ені 2а. Электрон қозғалысы бір өлшемді болғандықтан (ОХ осі бойымен), толқындық функция тек х осіне тәуелді болады және Лаплас операторының түрі 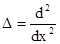. Е<0 екенін ескеріп, Шредингер теңдеуін І, ІІІ аймақтар және ІІ аймақ үшін мына түрде жазамыз:

I және III: 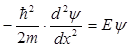, (11.7)

II: . (11.8)

(11.7) теңдеуін келесі түрде жазайық

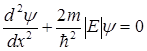және (11.9)

деп белгілейік. Олай болса І және ІІІ аймақтар үшін Шредингер теңдеуі мына түрге келеді

. (11.10)

Бұл теңдеудің шешуі келесі түрдегі толқындық функция болып табылады:

. (11.11)

ψ(х) функциясы шекті функция, олай болса х=±¥ мәндерінде ψ(х) шекті болуы үшін А=В=0 болуы керек, яғни І- және ІІІ- аймақтар үшін y(х)=0. Олай болса |y|²=0, ал мұның мағынасы І- және ІІІ- аймақтардағы электронды байқау ықтималдығы нөлге тең екенін білдіреді.

Енді потенциалдық шұңқыр ішіндегі (ІІ аймақ) электрон қозғалысын қарастырайық. Ол үшін (11.8) теңдеуін мына түрде жазайық

, (11.12)

мұндағы

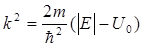. (11.13)

ІІ аймақ үшін Шредингер теңдеуін аламыз, |x|<a

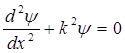. (11.14)

Бұл (11.14) теңдеуінің шешімі келесі түрдегі толқындық функция болады

, (11.15)

мұндағы С және D – шекаралық шарттардан анықталатын тұрақты коэффициенттер. Толқындық функция үздіксіз болу керек, сондықтан І және ІІ аймақтар шекарасы үшін

y_І(- a)=y_ІІ(- a) шарты орындалуы керек, ал ІІ және ІІІ аймақтар шекарасы үшін y_ІІ(a)=y_ІІІ(a) шарты орындалуы керек. Толқындық функцияның үздіксіз шарттарынан потенциалдық шұңқырдың шекарасында келесі шарттар шығады

. (11.16)

Алынған (11.16) теңдеулерін мүшелеп қосып coska =0 аламыз, ал бұл 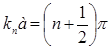кезінде орындалады, мұндағы n=0,1,2,… Толқындық сан 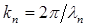деп есептеп, мына теңдеуді аламыз:

(11.17)

Бұл, потенциалдық шұңқырдың еніне де-Бройлдың жарты толқын ұзындығының тақ саны келетіндігін көрсетеді. Табылған k_n мәнін (11.13)-ке қойып, мынаны аламыз;

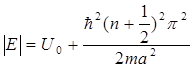. (11.18)

Соңғы өрнек, потенциалдық шұңқырдағы электрон n бүтін санына байланысты энергияның дискретті мәндерін қабылдауы мүмкін деген қортындыға келтіреді және энергияның кез-келген мәндеріне ие болуы мүмкін емес. Басқаша айтқанда, потенциалдық шұңқырдағы электрон, классикалық физикадағы көз-қарастан бөлек, дискретті энергетикалық күйлерде болады.

(11.16) теңдеуді мүшелеп алып, sіnka =0, яғни k_nа = np аламыз. Соңғы өрнектен

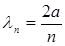. (11.19)

Бұл өрнектен, потенциалдық шұңқырдың еніне толқын ұзындығының бүтін саны дәл келетіндігін көрсетеді. (11.13) теңдеуін ескеріп, потенциалдық шұңқырдағы электрон энергиясы үшін мынаны табамыз:

. (11.20)

Бұл жағдайда да (11.18) сияқты энергия дискретті мәндерді қабылдайды. Алынған Шредингер теңдеуінің шешімі арқылы потенциалдық шұңқырдағы электрон үшін мынадай қортынды шығаруға болады: потенциалдық шұңқырдағы электронның энергиясы мен де-Бройль толқын ұзындығы кез-келген мәндерді қабылдамайды, олар тек қатаң түрде дискретті мәндерді қабылдайды.

Берілген есепті қарастыру кезінде потенциалдық шұңқырдың шекарасында толқындық функция нолге тең болады деп есептедік. Шын мәнінде, потенциалдық шұңқыр шекарасындағы электронның де-Бройль толқыны өзін әртүрлі сыну көрсеткіштері бар екі ортаның шекарасындағы электромагниттік толқындар сияқты сезінеді. Электромагниттік толқындар екінші ортаға өту шекарасында біршама шағылатындығы және сынатындығы белгілі. Потенциалдық шұңқыр шекарасындағы де-Бройль толқыны да өзін сол сияқты сезінеді, яғни потенциалдық шұңқыр шекарасының сыртында электронды байқ

Дата добавления: 2014-01-20