Пример-метафора. Продолжая метафору частицы, перемещающейся по кривой, можно сказать, что у нее на пути вдоль параметрической кривой не должно быть остановок (кроме начала и

Продолжая метафору частицы, перемещающейся по кривой, можно сказать, что у нее на пути вдоль параметрической кривой не должно быть остановок (кроме начала и конца) и внезапного изменения направления.

Для того чтобы представить направление движения частицы, можно мысленно "укрепить" на ней стрелку, которая непрерывно указывает направление движения вдоль параметрической кривой.

На математическом языке стрелка на частице называется касательной. Если касательная в соседних точках не меняет внезапно своего направления, такую кривую считают гладкой (рис. 12.4).

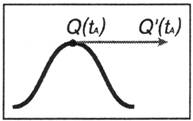
Рис. 12.4. Касательная на гладкой кривой

Если «на кривой имеется излом, то направление касательной в точке Q меняется практически мгновенно (рис. 12.5).

Рис. 12.5. Касательная на кривой с изломом

Теперь мы должны подробнее познакомиться с основами построения гладких кривых, применяющихся в векторной компьютерной графике. Начнем с NURBS-кривых, которые являются более общим (а соответственно, и более сложным) случаем таких кривых.

Дата добавления: 2014-01-20