Контрольные точки

NURBS-кривая

Обсуждение стоит начать с объяснения термина NURBS, который является аббревиатурой (сокращением) и расшифровывается как Non-Uniform Rational B-spline, где:

"Non-Uniform" (неоднородный) означает, что область влияния контрольной точки на форму кривой может быть различной. Это очень важное свойство для моделирования иррегулярных кривых.

"Rational" (рациональный) означает, что математическое выражение, описывающее форму моделируемой кривой, есть отношение двух полиномов.

Эта особенность позволяет точнее моделировать различные кривые, например, конические сечения.

"B-spline" (basis spline, базовый сплайн) — способ математического описания кривой интерполяцией между тремя и более контрольными точками.

Замечание

Кривые Безье являются специальным (частным) случаем В-сплайна.

Для начала вспомним, что в определении параметрической кривой левая часть выражения, описывающая функцию q, выглядит так:

q(t) =...,

где t — параметр, представляющий заданный набор значений определенного диапазона, как правило, от 0 до 1. Используя эти значения, получают последовательность пар {х, у}, по которым строится моделируемая кривая (рис. 12.6).

Рис. 12.6. Пример построения параметрической кривой

В указанном выше выражении не определена правая часть, т. е. собственно параметрическое уравнение, а точнее, параметрические уравнения.

Одной из основополагающих особенностей NURBS-кривой является то, что ее форма определяется расположением множества контрольных точек (control points). На рис. 12.7 эти точки обозначены как Bi.

Замечание

Контрольные точки соединены для наглядности прямыми линиями. Эта ломаная линия получила название управляющего многоугольника (control polygon).

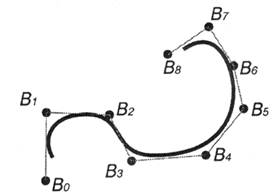
Рис. 12.7. Множество контрольных точек, определяющих параметрическую кривую

Эта особенность NURBS-кривой важна, поскольку позволяет локализовать изменение формы кривой перемещением отдельных контрольных точек без изменения формы всей кривой в целом (рис. 12.8).

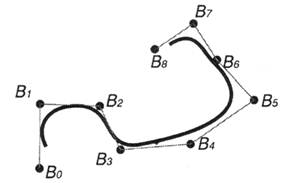
Рис. 12.8. Изменение формы фрагмента кривой, вызванное перемещением контрольной точки

Каждая контрольная точка определяет форму только той части кривой, которая находится в ее окрестности, и оказывает меньшее воздействие или вовсе не влияет на форму оставшейся части кривой.

Дата добавления: 2014-01-20