Математические основы векторной графики

В векторной графике основным элементом изображения является линия. В растровой графике тоже есть линии, но они рассматриваются как комбинации точек. Для каждой точки линии в растровой графике отводится одна или несколько ячеек памяти до 4^х (чем больше цветов могут иметь точки, тем больше ячеек им выделяется). Следовательно, чем длиннее растровая линия, тем больше памяти она занимает. В векторной графике объем памяти, занимаемый линией, не зависит от размеров линии, т.к. линия представляется в виде формулы (в виде нескольких параметров). Что бы вы ни делали с этой линией, меняются только ее параметры, хранящиеся в памяти. Количество же ячеек остается неизменным для любой линии.

В основе векторной графики лежат математические представления о свойствах геометрических фигур (прежде всего математическое представление линии).

Первая фигура Точка (узел) – задается двумя числами (х, у), определяющими ее положение относительно начала координат.

Прямая линия – достаточно двух параметров, т.е. уравнения у = bх + а. Зная параметры b и а, всегда можно нарисовать бесконечную прямую линию в известной системе координат.

Отрезок прямой – для задания надо знать еще два параметра, координаты х₁ и х₂, начала и конца отрезка, поэтому для описания отрезка прямой линии необходимы 4 параметра.

Кривая второго порядка – это гиперболы, эллипсы, окружности, т. е. линии, уравнения которых не содержат степеней выше второй и не имеющих точек перегиба. Общая формула кривой второго порядка:

х² + а₁у² + а₂ ху + а₃ х +а₄ у + а₅ = 0

5 параметров достаточно для описания бесконечной кривой второго порядка. Для записи отрезка кривой второго порядка необходимо 7 параметров.

Кривая третьего порядка – линии, уравнения которых не содержат степеней выше третей и имеют точку перегиба (функция у = х³ парабола).

х³ + а₁у³ + а₂х²у + а₃ху² + а₄х² + а₅у² + а₆ху + а₇х + а₈у +а₉ = 0

Для записи кривой третьего порядка достаточно 9 параметров. Для задания отрезка кривой третьего порядка, надо иметь 11 параметров.

Кривые Безье. Кривые третьего порядка соответствуют тем линиям, которые мы наблюдаем в живой природе, поэтому в качестве основных объектов векторной графики используются именно такие линии. Рисовать кривую третьего порядка по заданным коэффициентам ее уравнения – занятие утомительное. В векторной графике применяют особый вид кривых третьего порядка – кривые Безье. В начале 70-х годов профессор Пьер Безье, проектируя на компьютере корпуса автомобилей Рено, впервые применил для этой цели особый вид кривых, описываемых уравнением третьего порядка (функции Безье).

В настоящее время кривые Безье присутствуют в любом графическом пакете. Все компьютерные шрифты состоят из кривых Безье. Кривые Безье используются и в растровой графике. Так, в программе Photoshop используется термин контур, базирующийся на кривых Безье. Именно с помощью этого инструмента вы можете выделить на фотографии нужный объект (например, для его вырезания), который будет использован при создании фотомонтажа.

Отрезки кривых Безье описываются 8 параметрами, а не 11, как кривые третьего порядка. Метод построения кривой Безье основан на использовании пары касательных, проведенных к линии в точках ее концов. На практике эти касательные выполняют роль рычагов, с помощью которых линию изгибают так, как это необходимо. На форму линии влияет не только угол наклона касательной, но и длина ее отрезка.

Отрезками такой кривой можно создавать сколь угодно сложный контур. В этом случае он будет состоять из набора кривых Безье. В местах сочленений отрезков линия может иметь изломы, но с помощью функции сглаживания управляющие точки соседних отрезков легко выстраиваются в одну линию, после чего излом исчезает.

Появление кривых Безье вызвало переворот в видео и трехмерной графике, т.к. до их появления контуры компьютерных персонажей были ломанными, поверхности – граненными, а движение – прерывистым. Кривые Безье позволили реализовать наиболее общий и интуитивно понятный способ управления движением.

Объекты векторной графики

Линии. Все, что есть в векторной иллюстрации, состоит из элементарных объектов векторной графики линий. Простейшие объекты соединяются в более сложные. Объект прямоугольник можно рассматривать как четыре связанные линии, куб можно рассматривать либо как 12 связанных линий, либо как 6 связанных прямоугольников. Иллюстрация составляется из простых объектов, как из кубиков.

Процесс рисования в векторных редакторах фактически сводится к созданию контуров нужной формы и приданию им определенных заливок и обводок. Построение линии предполагает также задание ряда дополнительных атрибутов, определяющих ее основные свойства: форму, толщину, цвет, стиль (сплошная, пунктирная и т.п.). Количество атрибутов зависит от вида линии. Контур понятие математическое, и толщины он не имеет. Чтобы сделать контур видимым, ему придают обводку – линию заданной толщины и цвета, проведенную строго по контуру. По умолчанию всем новопостроенным линиям задается одинаковая толщина, однако по желанию обводку можно изменить – создать пунктирную, градиентную или художественную.

Узлы (Опорные точки). Узел является другим основным элементом векторной графики. В векторных редакторах форму контура изменяют путем манипулирования узлами. Это можно сделать следующими способами:

1. перемещением узлов; 2. изменением свойств узлов, атрибутов связанных с ними касательных линий и опорных точек; 3. добавлением или удалением узлов. При выделении узловой точки криволинейного сегмента у нее появляются одна или две управляющие точки, соединенные с узловой точкой касательными линиями. Рис.5.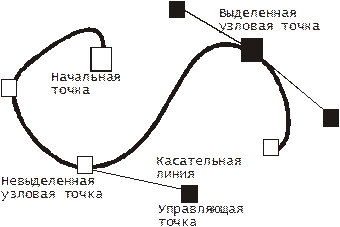
Термины узлов кривых Безье.

Управляющие точки отмечены черными закрашенными точками. Расположение касательных линий и управляющих точек определяет длину и форму (кривизну) криволинейного сегмента, а их перемещение приводит к изменению формы контура.

Типы узловых точек. В CorelDraw узловые и управляющие точки перемещают с помощью инструмента Форма. Для этого достаточно щелкнуть инструментом Форма на соответствующей узловой или управляющей точке и перетащить их в нужном направлении. Вид касательных линий и соответственно методы управления кривизной сегмента в точке привязки определяются типом узловой точки. Различают три типа узловых точек:

1. Симметричный узел – оба отрезка касательных по обе стороны точки привязки имеют одинаковую длину и лежат на одной прямой, которая показывает направление касательной к контуру в данной узловой точке, т.е. кривизна сегментов с обеих сторон точки привязки одинакова.

Изменение положения управляющей точки приводит к соответствующему изменению угла наклона касательной к кривой. Изменение длины касательной линии с одной стороны точки привязки приводит к соответствующему изменению второй касательной, что изменяет радиус кривизны линии в точке привязки. В CorelDraw симметричные узлы создаются автоматически при рисовании кривых инструментом Безье методом перетаскивания.

2. Гладкий узел – оба отрезка касательных линий по обе стороны опорной точки лежат на одной прямой, которая показывает направление касательной к кривой в данной точке, но длина управляющих линий разная. Следовательно, кривизна криволинейных участков, прилегающих к этой опорной точке, различна с разных сторон.

Изменение длины касательной линии с одной стороны опорной точки путем перемещения управляющей точки приводит к изменению радиуса кривизны этого криволинейного сегмента с одной стороны узловой точки. При этом длина второго отрезка касательной линии не изменяется.

3. Острый угол – касательные линии с разных сторон опорной точки не лежат на одной прямой. Поэтому два криволинейных сегмента, прилегающих к опорной точке, имеют различную кривизну с разных сторон узловой точки, и контур в этой точке образует резкий излом. Для острого угла радиус кривизны и угол наклона касательной для каждого криволинейного сегмента можно регулировать независимо друг от друга соответствующим изменением длины и угла наклона касательной линии для каждого, прилегающего к опорной точке криволинейного сегмента в отдельности. В частности, один из отрезков касательных может быть равен нулю.

Примитивы. Наряду с разнообразными кривыми, векторные редакторы имеют в своем составе специальные инструментальные средства для создания простых форм (графических примитивов), что упрощает построение сложных объектов. К основным примитивам присутствующих во всех векторных редакторах относятся: прямоугольник (квадрат), эллипс (круг), многоугольник (звезда), спираль. В графических редакторах предусмотрена возможность управления числом сторон многоугольника и количеством вершин у звезд.

Часто наряду со своим прямым назначением простые формы используют в качестве исходных заготовок для создания на их базе более сложных объектов. В этом случае для последующего редактирования созданных заготовок необходимо привлечение технологии редактирования кривых Безье с помощью перемещения узлов и управляющих точек. Для осуществления этой процедуры требуется выполнить преобразование примитивов в кривые Безье, поскольку их математическое описание отличается от формул, заложенных в построение кривых Безье. В CorelDraw преобразование в кривые выполняется командой Компоновать/Преобразовать в кривые.

Дата добавления: 2014-01-20