Метод решения СЛАУ с постолбцовым выбором главного элемента

ЛЕКЦИЯ 17.

Метод Гаусса решения СЛАУ на кластере.

Рассматриваются системы вида:

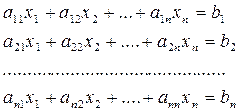
или иначе, системы векторно-матричных уравнений

Ax=b.

Наиболее известным методом решения систем данного вида является метод Гаусса, состоящий в последовательном исключении неизвестных. Будем поэтапно приводить систему к треугольному виду, исключая последовательно сначала x 1 из второго, третьего,…, n -го уравнений, затем x 2 из третьего, четвертого,…, n -го уравнения преобразованной системы и так далее. На первом этапе заменим второе, третье,…, n -ое уравнения на уравнение, получающееся сложением этих уравнений с первым, умноженным соответственно на На втором этапе проделываем такие же операции, как и на первом, с подсистемой исходной системы, получающейся исключением первого уравнения и т.д.

Продолжая этот процесс, на (n -1)–ом этапе так называемого прямого хода ме-

тода Гаусса данную систему приведем к треугольному виду:

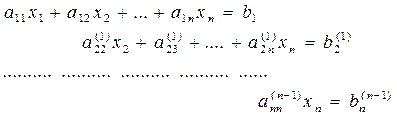
Коэффициенты этой системы могут быть получены из коэффициентов данной системы последовательным пересчетом по формулам:

где верхний индекс k (номер этапа) изменяется от 1 до (n -1), нижние индексы

i и j (в любой очередности) – от k+ 1 до n.

Треугольная структура системы позволяет последовательно одно за

другим вычислять значения неизвестных, начиная с последнего:

Этот процесс последовательного вычисления неизвестных называют обратным ходом метода Гаусса. Он определяется одной формулой

где k полагают равным n, n- 1, …,2,1 и сумма по определению считается равной нулю, если нижний предел суммирования у знака суммы имеет значение больше верхнего.

Таким образом, алгоритм Гаусса выглядит так:

1. Для

2. Найти что , обменять строки и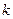

3. Для :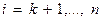

4. ,

5.

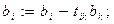
6. Для :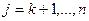

7.

8.

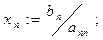
9. Для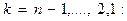

10.

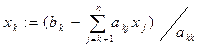
Подав на его вход квадратную матрицу коэффициентов при неизвестных исходной системы и вектор свободных членов, и выполнив три вложенных цикла прямого хода и один цикл вычислений обратного хода, на выходе получим вектор –решение.

Чтобы уменьшить влияние ошибок округления на каждом этапе прямого

хода уравнения системы обычно переставляют так, чтобы деление производи-

лось на наибольший по модулю в данном столбце (обрабатываемом подстолб-

це) элемент. Числа, на которые производится деление в методе Гаусса, называ-

ются ведущими или главными элементами. Отсюда название – метод Гаусса с

постолбцовым выбором главного элемента (или с частичным упорядочиванием

по столбцам).

Частичное упорядочивание по столбцам требует внесения в алгоритм сле-

дуюших изменений: между строками 1 и 2 нужно сделать вставку:

• Найти такое m≥k, что │ amk │= max{│ aik │} при i≥k,

• иначе поменять местами bk и bm, akj и amj при всех j=k,…,n.

Сравнение метода единственного исключения с компактной схемой Гаусса. Кроме изложенного выше метода Гаусса единственного исключения существуют и другие методы решения СЛАУ, например, метод LU- факториза-

ции матриц, называемый компактной схемой Гаусса. Покажем, в чем сходство

этих методов. В случае компактной схемы матрица представляется в виде про-

изведения A=LU, где L – нижняя треугольная матрица, U – верхняя треугольная матрица.

После нахождения матриц система Ax=b заменяется системой LUx=b и решение СЛАУ выполняется в два этапа:

Ly=b

Ux=y

Таким образом, решение данной системы с квадратной матрицей коэффи-

циентов свелось к последовательному решению двух систем с треугольными

матрицами коэффициентов.

Получим сначала формулы для вычисления элементов yi. Для этого запишем уравнение Ly=b в развернутом виде:

Значит все yi могут быть последовательно найдены при i= 1, 2, …., n по

формуле

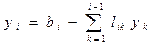
Развернем теперь векторно-матричное уравнение Ux = y:

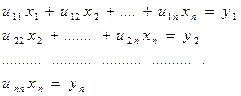
Отсюда значения неизвестных xi находятся в обратном порядке, то есть при i=n, n-1, …2, 1, по формуле

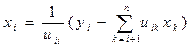
Сходство метода Гаусса (МГ) с компактной схемой Гаусса (КСГ) состоит в том, что элементы матриц L и U в КСГ соответствуют по величине коэффици-

ентам, получаемым при разложении в МГ.

Методы блочного размещения данных в кластере. Теперь будет рассмотрено размещение матрицы по слоям в машинах с распределенной памятью с целью наиболее эффективного выполнения гауссового исключения.

Двумя главными затруднениями в выборе размещения данных для гауссова исключения являются:

• Баланс нагрузки, то есть обеспечение загрузки всех процесоров на протяжении всего времени вычислений

• Возможность использования BLAS3 на одном процессоре, чтобы подсчи

тать иерархию памяти на каждом процессоре

Примечание. Уровенень BLAS1 библиотеки BLAS используется для вы-

полнения операций вектор-вектор, уровенень BLAS2 – для выполнения мат-

рично-векторных операций, уровенень BLAS3 – для выполнения матрично-

матричных операций.

Рассмотрим варианты секционирования матриц. Для удобства мы будем

нумеровать процессоры от 0 до р-1, и матричные столбцы (или строки) от 0 до

n-1. Во всех случаях каждая подматрица обозначается номером процессора (от

0 до 3), который содержит ее. Процессор 0 представлен затененными подмат-

рицами.

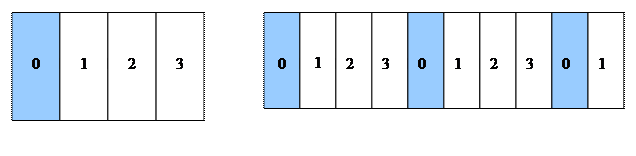
Рассмотрим перый вариант – размещение по столбцам матрицы А (Column Blocked Layout). При этом разбиении столбец i хранится в последнем незаполненном процессоре, если считать, что c=ceiling(n/p) есть максимальное число столбцов, приходящееся на один процессор и вести счет столбцов слева направо. Это разбиение не позволяет сделать хорошую балансировку нагрузки, поскольку как только первые с столбцов завершены, процесор 0 становтся свободным до конца вычислений. Размещение по строкам (Row Blocked Layout) создает такую же проблему.

Другой вариант – циклическое размещение по столбцам (Column Cyclic

Layout) использует для решения проблемы простоев назначение столбца i

процессору с номером i mod p. Однако, тот факт, что хранятся одиночные

столбцы, а не их блоки, означает, что мы не можем использовать BLAS2 для

факторизации A(ib:n,ib:end) и возможно не сможем использовать BLAS3 для

обновления A(end+1:n,end+1:n). Циклическое размещение по строкам (Row Cyclic Layout) создает такую же проблему.

Третье размещение - столбцовый блочно- циклический вариант (Column

Block Cyclic Layout) есть компромисс между двумя предыдущими. Мы выбира-

ем размер блока b, делим столбцы на группы размера b, и распределяем эти

группы циклическим образом. Это означает, столбец i хранится в процессоре

(последний (i/b)) mod p. В действительности это распределение включает пер-

вые два как частный случай b=c=ceiling(n/p) и b=1, соответственно.

Есть еще одно размещение – блочное смещенное размещение (Block Skewed Layout. В нем имеется особенность, что каждая строка и каждый столбец распределяются среди всех р процессоров. Так называемый винтовой (p-fold) параллелизм пригоден для любых строчных и столбцовых операций.

Варианты LU Decomposition. Возможны три естественных варианта для LU decomposition: левосторонний поиск, правосторонний поиск и метод Краута.

• left-looking вариант вычисляет блочный столбец зараз, используя ранее

вычисленные столбцы.

• right-looking вариант вычисляет на каждом шаге строчно-столбцовый

блок (block row column) и использует их затем для обновления заключи-

тельной подматрицы. Этот метод называется также рекурсивным алго-

ритмом. Термины right and left относятся к области доступа к данным.

• Crout ваприант представляет гибрид left- and right версий.

Дата добавления: 2014-01-20