Теоретические результаты

Инварианты программ

Программы, интерпретированные над алгебрами данных

Пусть A – алгебра с сигнатурой операций S = <s₁, …, s_k> и носителем A. Пусть, далее, X = < x₁, …, x_n > - вектор переменных, которые мы интерпретируем как переменные программы. Для краткости мы будем называть X памятью программы, а векторы a = < a₁, …, a_n>, a_i Î A - состояниями памяти. Множество U = Aⁿ образует пространство - универсум состояний памяти программы. Вычисляющий оператор – это отображение F: U à U, определенное покоординатно системой присвоений

x₁:= f₁(X), …, x_n:= f_n(X) (2)

Вычисляющий оператор мы будем записывать в векторной форме X:= F(X), а вектор координатных функций (вычислений) – в форме F = <f₁, …, f_n>. Отметим, что в таких обозначениях вычисляющий оператор интерпретируется как одновременное присвоение вектору переменных значений – правых частей покоординатных операторов присвоений.

Мы будем говорить, что программа P определена линейно (интерпретирована над векторным про­странством), если A – некоторое поле (область целостности), а все ее вычисляющие операторы имеют вид

X:= F*X + b, (3)

где F – линейный оператор, действующий в векторном пространстве U, а b Î U.

Мы будем говорить, что программа P определена полиномиально (интерпретирована над полиномиальным кольцом), если A – некоторое поле (область целостности), а все ее вычисляющие операторы имеют вид

X:= F(X), (4)

гдеf_i Î A [X], т.е. многочлены с коэффициентами из A.

Мы будем говорить, что программа P определена рационально (интерпретирована над полем рациональных выражений), если A – некоторое поле, а все ее вычисляющие операторы имеют вид

X:= F(X), (5)

гдеf_i Î A (X), т.е. рациональные выражения с коэффициентами из A.

Условия определяются как предикаты в некотором специальном языке L условий. Во всяком случае, этот язык включает предикаты равенства и их отрицания (=, ¹).

Таким образом, программы, интерпретированные над линейными пространствами, на каждом шаге вычислений осуществляют линейные преобразования универсума состояний памяти U, программы, интерпретированные над полиномиальными кольцами – полино­миаль­ные преобразования U, а программы, интерпретированные над полем рациональных выражений - рациональные преобразования U.

Многочлен g(X) Î A[X] называется полиномиальным инвариантом программы P, если при любом начальном состоянии памяти a = < a₁, …, a_n>, если программа P завершает работу, для заключительного состояния памяти b выполняется равенство g(b) = 0.

Множество всех полиномиальных инвариантов рационально определенных программ образует радикальный идеал кольца A[X], который мы будем обозначать через .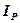

В дальнейшем мы будем рассматривать также множество всех элементов 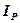, степени которых ограничены некоторой константой M. Множество таких многочленов образует векторное пространство, которое обозначается через 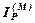. Понятно, что .

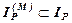Теорема 1. Если ch(A) = 0 и язык условий L включает предикаты равенства и их отрицания (=, ¹), проблема построения базиса 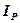в классе линейно определенных программалгоритмически неразрешима.

Понятно, что из этой теоремы сразу следует неразрешимость рассматриваемой проблемы для всех классов программ, рассматриваемых в настоящей лекции. Поэтому в дальнейших результатах условия в программах приходится игнорировать, считая программы абсолютно недетерминированными. Список (1) операций над программами при этом редуцируется до

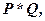
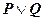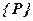, . (6)

Основной результат [3] настоящей работы, состоит в следующем:

Теорема 2. Пусть P - программа, интерпретированная над полиномиальным кольцом A[X], и .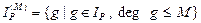

Тогда:

а) Проблема принадлежности 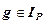алгоритмически разрешима.

б) Проблема построения базиса векторного пространства 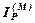алгоритмически разрешима.

Доказательство. (Индукция по структуре регулярного выражения, представляющего программу)

Пусть все вычисляющие операторы, встречающиеся в программе P, и .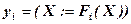

Доказательство утверждения а) будем вести индукцией по структуре редуцированной программы P, т.е. по структуре ее регулярного выражения в сигнатуре (6), в которой вычисляющие операторы – суть атомы .

Пусть w = y_j1*y_j2*…_*y_jk – программа, представляющая собою последо­ва­тельность вычисляющих операторов. Мы будем говорить, что w Î P, если P допускает вычисления, описанные w. Mы будем также называть w словом P. Собственно программа P ассоциируется тогда со множеством принадлежащих ей слов (множество слов – это множество всевозможных путей вычислений P).

Введём следующие обозначения. Через g(w), 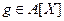, обозначим многочлен 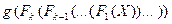, а через 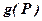- множество многочленов вида g(w), 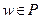. Идеал, порожденный множеством 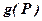, обозначим через .

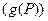Мы покажем, что для каждой программы 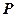существует и может быть эффективно построено конечное подмножество слов 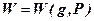такое, что 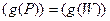. Поскольку g - инвариант программы P тогда и только тогда, когда g(w) = 0 для любого 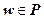, проверка инвариантности g сведётся к проверке равенств g (w) = 0, .

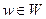1. (базис индукции) 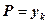. Тогда .

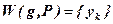2. (шаг индукции)

а).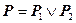

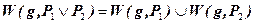
б)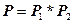

Пусть 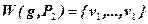. Поскольку из 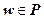следует 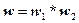, где 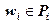имеем 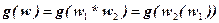, откудa

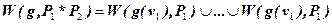(7)

в)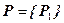

Тогда , где E – обозначение тождественного вычисляющего оператора. Рассмотрим последовательность идеалов:

Поскольку кольцо A[X] нетерово, эта последовательность стабилизируется на некотором номере 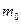. Покажем, что 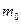- наименьшее натуральное число такое, что

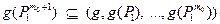(8)

В самом деле, из (7) следует

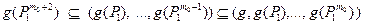
поэтому из равенства 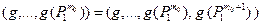следуют равенства 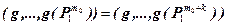для любого натурального k, откуда

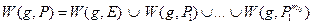(9)

Поскольку проблема принадлежности 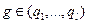алгоритмически разрешима, формулы (6) - (8) описывают рекурсивный алгоритм построения 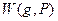. Утверждение а) доказано.

Для доказательства утверждения б) необходимо рассмотреть многочлен 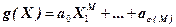степени M с неопределенными коэффициентами и для него построить множество 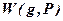. Поскольку кольцо 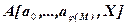также нетерово, это построение можно осуществить с помощью алгоритма пункта а).

Пусть 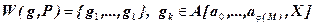. Система равенств 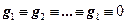определяет систему линейных уравнений над A с неизвестными , фундамен­таль­ная система решений которой задаёт искомый базис .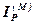

Дата добавления: 2014-01-20