Основные задачи и алгоритмы

Из доказательства теоремы 2а) видно, что основной алгоритмической проблемой, которую нужно решить при реализации соответствующего алгоритма, является проблема

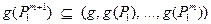
Иными словами, задача сводится к тому, чтобы распознать принадлежность некоторого многочлена полиномиальному идеалу, заданному своим базисом. Эта задача является клас­сической задачей теории полиномиальных идеалов, и для ее решения лучше всего использовать базисы Гребнера полиномиальных идеалов.

Таким образом, все идеалы, которые строятся в алгоритме теоремы 2а), должны быть представлены своими базисами Гребнера. В дальнейшем мы будем обозначать тот факт, что идеал I представлен базисом Гребнера f₁, …, f_k, равенством

I = (f₁, …, f_k )_Gr.

Базис Гребнера идеала I мы будем обозначать через Gr(I).

Наш алгоритм теоремы 1а) должен быть основан на решении следующих задач:

1. Для I = (f₁, …, f_k )_Gr , J = (g₁, …, g_l )_Gr найти K = (f₁, …, f_k,h₁ ,..., h_m)_Gr

2. Для I = (f₁, …, f_k )_Gr, вычисляющего оператора X:= H(X), найти J = (g₁,..., g_l )_Gr, т.е. найти Gr((f₁(H(X)), …, f_k(H(X)))).

3. Для I = (f₁, …, f_k )_Gr , J = (g₁, …, g_l )_Gr распознать I Í J.

Задачи 1 и 3 – классические задачи теории полиномиальных идеалов, решение которых в терминах базисов Гребнера хорошо известно. Для решения задачи 2 можно восполь­зоваться общим алгоритмом пополнения, который строит базис Гребнера по произвольному конечному множеству полиномов или использовать формулы, аналогичные формулам (11), приведенным для рационально определенных программ. Рассмотрим теперь вопросы, связанные с реализацией алгоритма теоремы 1б). Отме­­­тим, что из метода доказательства следует, что искать инварианты можно, задавая их в виде полиномиальных форм, т.е. многочленов «специального» вида с неопределенными коэффициентами. Например, можно определить общий вид искомых инвариантов как линейную комбинацию нескольких многочленов с неопределенными коэффициентами:

g(X) = a₁*g₁(X)+…+a_k*g_k(X) (9)

Если, например, требуется искать линейные инварианты, следует положить

g₁= x₁,..., g_n = x_n, g_n+1 = 1. (10)

Можно, к примеру, искать все инварианты вида g(X) = a₁*x₁² +…+a_n * x_n² и т.п.

Поскольку вычисляющие операторы оставляют неопределенные коэффициенты неподвижными, алгоритмы теоремы 2а) следует применять покординатно к вектору многочленов (g₁(X), … g_k(X)). Базисы Гребнера следует строить отдельно для многочленов g₁(X), … g_k(X), а условие обрыва возрастающих цепочек п. в) алгоритма теоремы 1а) применять ко всему вектору идеалов (I₁,..., I_n). Таким образом, построение конечного множества слов из символов y_i вычисляющих операторов при анализе программы P = {P₁} заканчивается при таком значении m, при котором стабилизируются все координаты вектора идеалов (I₁,..., I_n).

Дата добавления: 2014-01-20