КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 0
|
|
|
|
|
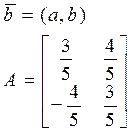
Пример 1. ( линейный оператор с характеристическим многочленом 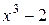 )
)
Рассмотрим линейный оператор с матрицей
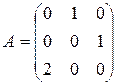 ,
,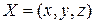 .
.
Покажем, что рациональное выражение
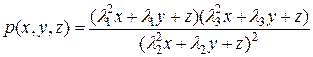 (2)
(2)
где 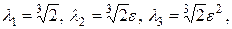 а
а 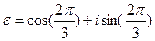 - первообразный корень степени 3 из 1 – L–инвариант этого оператора.
- первообразный корень степени 3 из 1 – L–инвариант этого оператора.
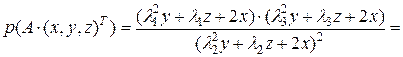
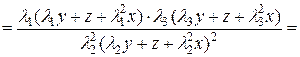
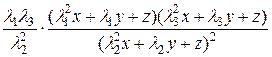 =
=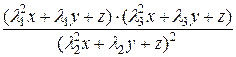
Определение 2. Пусть 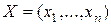 ,
, 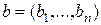 - два набора переменных. Линейным циклом мы называем фрагмент императивной программы вида
- два набора переменных. Линейным циклом мы называем фрагмент императивной программы вида
X:= b;
While Q(X, b) do X:= A*X
Замечание. Операторы X:=b, X:=A*X интерпретируются как одновременные присвоения переменным левых частей значений правых частей. В дальнейшем условие Q(X, b) мы будем игнорировать, считая линейный цикл бесконечным, а его выполнение недетерминированным. Т.о. мы рассматриваем циклы вида
X:= b;
While True|False do X:= A*X
Предложение 1. Если 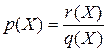 - L-инвариант линейного оператора
- L-инвариант линейного оператора  , многочлен
, многочлен 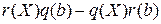 - инвариант линейного цикла над полем
- инвариант линейного цикла над полем 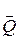 . Такие инварианты циклов мы будем также называть L-инвариантами (линейных циклов).
. Такие инварианты циклов мы будем также называть L-инвариантами (линейных циклов).
Пример 2. (линейный цикл с оператором примера 1)
Линейный цикл, соответствующий оператору  , имеет вид
, имеет вид
(x, y, z):= (a, b, c);
While True|False do (x, y, z):= (y, z, 2*x)
L-инвариант этого цикла определен формулой (2):
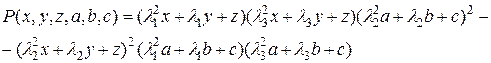 (3)
(3)
Отметим, что L-инвариант цикла 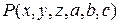 определен над полем
определен над полем 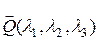 . Однако ему соответствует набор L-инвариантов с коэффициентами из поля
. Однако ему соответствует набор L-инвариантов с коэффициентами из поля 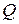 , которые можно построить, приведя (3) к каноническому виду – многочлену от
, которые можно построить, приведя (3) к каноническому виду – многочлену от 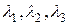 , а затем – к многочлену от
, а затем – к многочлену от 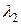 , используя соотношение
, используя соотношение 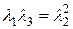 и соотношения Виета. Продемонстрируем технику вычисления L-инвариантов над полем
и соотношения Виета. Продемонстрируем технику вычисления L-инвариантов над полем 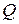 .
.
Введем обозначения
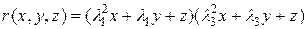 ,
, 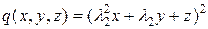
Многочлены 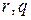 определены над полем
определены над полем 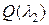 . Вычислим
. Вычислим 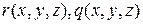 в виде многочленов от
в виде многочленов от 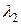 . Получим:
. Получим:
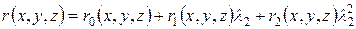 ,
, 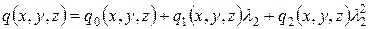 ,
,
где
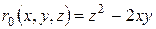 ,
, 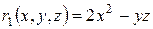 ,
, 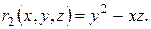
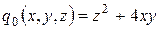 ,
, 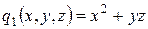 ,
, 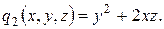 (4)
(4)
Дробь 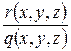 представима в виде многочлена от
представима в виде многочлена от 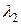 с коэффициентами из
с коэффициентами из 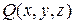 .
.
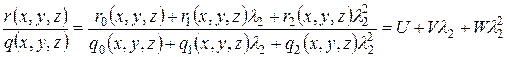 ,
,
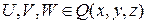 (5)
(5)
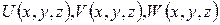 можно вычислить методом неопределенных коэффициентов, используя равенство (5). Осталось заметить, что
можно вычислить методом неопределенных коэффициентов, используя равенство (5). Осталось заметить, что 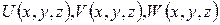 - L-инварианты оператора
- L-инварианты оператора  . В самом деле,
. В самом деле,
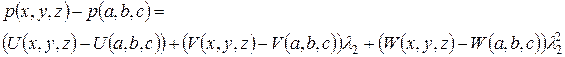
Поскольку 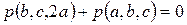 , имеем
, имеем
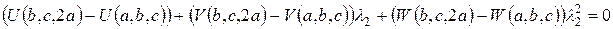

Ввиду линейной независимости векторов 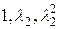 над
над 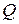
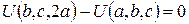 ,
, 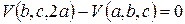 ,
, 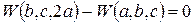 ,
,
т.е 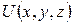 ,
, 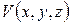 ,
, 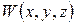 - L-инварианты над
- L-инварианты над 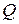 .
.
Отметим, что если переменным 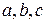 придать числовые значения, L-инвариант преобразуется в инвариант цикла.
придать числовые значения, L-инвариант преобразуется в инвариант цикла.
Метод построения L-инвариантов, который мы будем рассматривать, заключается в вычислении и анализе собственных значений и собственных векторов линейных операторов.
Предложение 2. Пусть 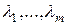 - собственные значения линейного оператора
- собственные значения линейного оператора  и
и 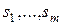 - соответствующие им собственные векторы сопряженного оператора
- соответствующие им собственные векторы сопряженного оператора 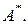 Предположим, что существуют такие целые числа
Предположим, что существуют такие целые числа 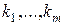 , что
, что
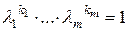 . (6)
. (6)
Тогда
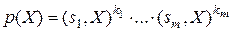 (7)
(7)
- L -инвариант линейного оператора  .
.
Доказательство. Пусть 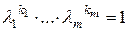 . Тогда
. Тогда 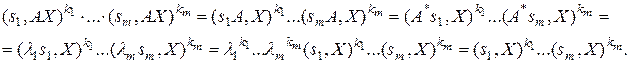
Соотношение (6) мы будем называть мультипликативным соотношением (между корнями характеристического многочлена), определяющим L -инвариант (7).
Пример 3 (продолжение примера 2). Рассмотрим метод предложения 2 применительно к примеру 2. Вычислим собственные числа оператора 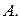
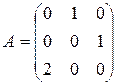 ,
, 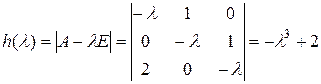 . Т.о. характеристический многочлен имеет вид
. Т.о. характеристический многочлен имеет вид 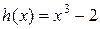 . Его корни -
. Его корни - 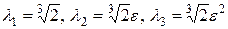 ,
, 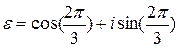 (
(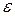 - первообразный корень степени 3 из 1).
- первообразный корень степени 3 из 1).
Вычислим далее собственные векторы матрицы 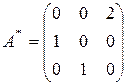 . Решим для этого систему однородных линейных уравнений
. Решим для этого систему однородных линейных уравнений 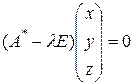 , причем вычисления будем осуществлять в поле
, причем вычисления будем осуществлять в поле 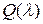 по модулю
по модулю 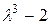 . Получим систему линейных уравнений
. Получим систему линейных уравнений
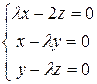 , ранг которой равен 2. Фундаментальное решение этой системы – вектор
, ранг которой равен 2. Фундаментальное решение этой системы – вектор 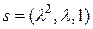 . Поэтому собственными векторами оператора
. Поэтому собственными векторами оператора 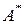 являются векторы
являются векторы
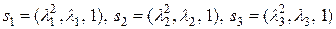 .
.
Легко установить, что 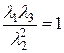 . Поэтому оператор
. Поэтому оператор  имеет L-инвариант (2).
имеет L-инвариант (2).
Следствие 1. Если характеристический (минимальный) многочлен 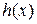 линейного оператора
линейного оператора  имеет свободный член, равный
имеет свободный член, равный 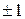 (т.е.
(т.е. 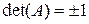 ), линейный оператор
), линейный оператор  обладает L -инвариантом.
обладает L -инвариантом.
Доказательство. Пусть 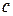 – свободный член многочлена
– свободный член многочлена 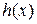 . Тогда
. Тогда 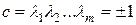 . Поэтому либо
. Поэтому либо 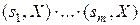 , либо (
, либо (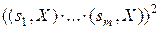 - L-инвариант оператора
- L-инвариант оператора  . Отметим, что коэффициенты этого полинома принадлежат
. Отметим, что коэффициенты этого полинома принадлежат 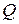 , поскольку они симметричны относительно перестановок корней
, поскольку они симметричны относительно перестановок корней 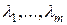 .
.
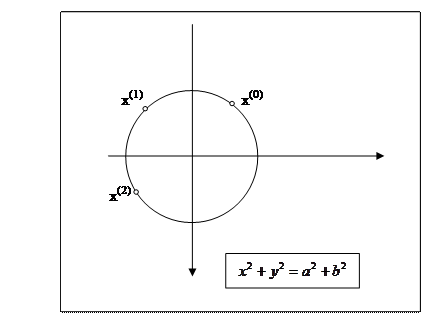
Пример 4. Цикл поворота точки плоскости 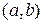 на угол
на угол 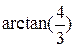 .
.
(x,y):= (a,b);
While True do (x, y):= (4/5*x - 3/5*y, 3/5*x + 4/5*y)
Вычислим собственные значения и собственные векторы оператора  :
:
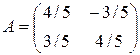 .
. 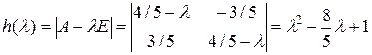 .
.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 407; Нарушение авторских прав?; Мы поможем в написании вашей работы!