
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Собственные полиномы жордановых клеток
|
|
|
|
..
..
Поскольку 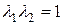 , L-инвариант оператора
, L-инвариант оператора  имеет вид
имеет вид
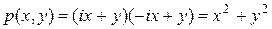 .
.
Инвариант цикла имеет вид 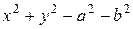 .
.
Пример 5. Цикл вычисления последовательности Фибоначчи, начиная с пары 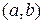 .
.
(x,y):= (a,b);
While True|False do (x, y):= (x + y, x)
Вычислим собственные значения и собственные векторы оператора 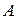 :
:
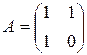 .
. 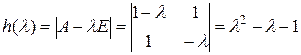 .
.
Поскольку 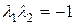 , L-инвариант оператора
, L-инвариант оператора 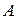 имеет вид
имеет вид
 .
.
Инвариантное соотношение цикла имеет вид 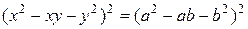 .
.
Следствие 2. Если характеристический (минимальный) многочлен  линейного оператора
линейного оператора 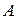 имеет вид
имеет вид  , линейный оператор обладает L -инвариантами.
, линейный оператор обладает L -инвариантами.
Доказательство. Корни 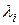 характеристического многочлена
характеристического многочлена  определены формулой
определены формулой 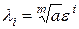 , где
, где 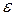 - первообразный корень степени
- первообразный корень степени  из 1. Легко видеть, что если
из 1. Легко видеть, что если 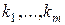 - целые числа такие, что
- целые числа такие, что 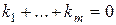 , то
, то 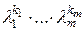 - некоторая степень
- некоторая степень 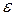 . В самом деле,
. В самом деле,
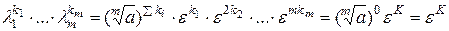 ,
,
где 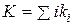 . Поэтому произведение
. Поэтому произведение 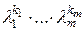 в подходящей степени равно 1.
в подходящей степени равно 1.
Итак, L-инварианты оператора 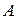 существуют и вычисляется аналогично тому, как это сделано в примере 3. В частности, L-инвариантами оператора
существуют и вычисляется аналогично тому, как это сделано в примере 3. В частности, L-инвариантами оператора 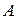 являются рациональные выражения
являются рациональные выражения
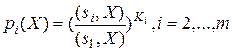 ,
,
где 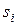 - собственные векторы
- собственные векторы 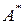 , а
, а  - наименьшие натуральные числа такие, что
- наименьшие натуральные числа такие, что 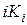 кратно
кратно  :
: 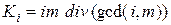 .
.
Предложение 3. Пусть 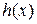 - многочлен от переменной
- многочлен от переменной 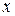 с рациональными коэффициентами и
с рациональными коэффициентами и 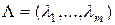 - все его корни из алгебраического замыкания
- все его корни из алгебраического замыкания 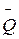 поля
поля 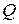 . Рассмотрим множество
. Рассмотрим множество 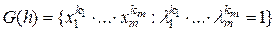
 - множество мономов из поля рациональных выражений
- множество мономов из поля рациональных выражений  (возможно, с отрицательными степенями), которые при подстановке
(возможно, с отрицательными степенями), которые при подстановке 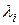 вместо
вместо 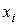 получают значение 1. Тогда
получают значение 1. Тогда 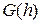 - мультипликативная абелева группа с конечным числом образующих.
- мультипликативная абелева группа с конечным числом образующих.
Доказательство. Каждому моному 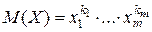 поставим в соответствие бином кольца
поставим в соответствие бином кольца 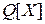
 следующим образом: моном
следующим образом: моном 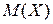 представим в виде дроби
представим в виде дроби 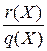 , в числителе которой запишем степени переменных с положительными показателями, а в знаменателе – степени переменных с отрицательными показателями, взятыми со знаком «минус»:
, в числителе которой запишем степени переменных с положительными показателями, а в знаменателе – степени переменных с отрицательными показателями, взятыми со знаком «минус»: 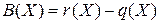 .
.
Группа 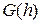 , очевидно, может быть определена и множеством выше определенных биномов:
, очевидно, может быть определена и множеством выше определенных биномов: 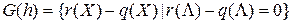 . Во множестве биномов
. Во множестве биномов 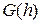 можно выделить конечное подмножество
можно выделить конечное подмножество  , которое образует базис идеала кольца
, которое образует базис идеала кольца 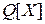 , порожденного множеством
, порожденного множеством 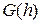 :
: 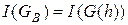 . Построим базис Гребнера этого идеала, опираясь на базис
. Построим базис Гребнера этого идеала, опираясь на базис  . Легко видеть, что S-полином пары биномов также является биномом. Кроме того, редукция бинома заключается в замене
. Легко видеть, что S-полином пары биномов также является биномом. Кроме того, редукция бинома заключается в замене  на
на 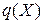 . Поэтому процесс построения базиса Гребнера приводит к конечному множеству биномов, которое мы будем обозначать через
. Поэтому процесс построения базиса Гребнера приводит к конечному множеству биномов, которое мы будем обозначать через 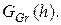 Каждый элемент
Каждый элемент 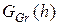 , в свою очередь, определяет моном рассматриваемого нами вида. Обозначим множество таких мономов через
, в свою очередь, определяет моном рассматриваемого нами вида. Обозначим множество таких мономов через 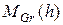 . Осталось показать, что
. Осталось показать, что 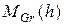 образует множество, порождающее группу
образует множество, порождающее группу 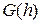 .
.
Пусть 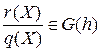 ,
,  . Обозначим через
. Обозначим через 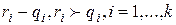 биномы из
биномы из 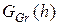 – элементы базиса Гребнера. (Обозначения переменных в формулах мы опускаем.) Поскольку
– элементы базиса Гребнера. (Обозначения переменных в формулах мы опускаем.) Поскольку 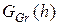 - базис Гребнера, бином
- базис Гребнера, бином 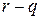 редуцируется к нулю с помощью элементов
редуцируется к нулю с помощью элементов 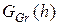 «исчерпыванием». Это означает, что на каждом шаге редуцирования существует такой номер
«исчерпыванием». Это означает, что на каждом шаге редуцирования существует такой номер 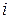 базисного элемента, что
базисного элемента, что 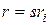 . Шаг редуцирования исчерпыванием состоит в следующем преобразовании:
. Шаг редуцирования исчерпыванием состоит в следующем преобразовании:  . Этому преобразованию поставим в соответствие следующее преобразование монома - элемента
. Этому преобразованию поставим в соответствие следующее преобразование монома - элемента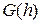 :
:
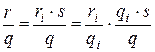
Таким образом, шаг редуцирования применительно к элементам 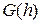 состоит в выделении в мономе
состоит в выделении в мономе 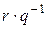 сомножителя
сомножителя 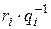 . Редуцированный бином, если это необходимо, следует переупорядочить так, чтобы первый его моном был больше второго. Это преобразование состоит в следующем:
. Редуцированный бином, если это необходимо, следует переупорядочить так, чтобы первый его моном был больше второго. Это преобразование состоит в следующем: 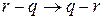 . Понятно, что после этого преобразования в мономе
. Понятно, что после этого преобразования в мономе 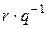 выделяются сомножители знаменателя:
выделяются сомножители знаменателя: 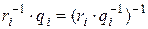 . Итак, мы показали, что процесс редуцирования исчерпыванием соответствует процессу разложения монома
. Итак, мы показали, что процесс редуцирования исчерпыванием соответствует процессу разложения монома 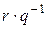 в произведение базисных мономов (возможно, с отрицательными показателями). Теорема доказана.
в произведение базисных мономов (возможно, с отрицательными показателями). Теорема доказана.
Пример 6 (Продолжение примера 3). Легко видеть, что для многочлена 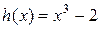 имеют место следующие мультипликативные соотношения между его корнями:
имеют место следующие мультипликативные соотношения между его корнями:
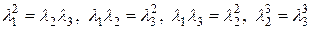
Этим соотношениям соответствуют биномы
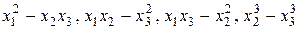 ,
,
которые образуют базис Гребнера идеала 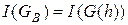 .
.
Следствие 1. Пусть 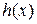 - многочлен от переменной
- многочлен от переменной 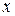 с рациональными коэффициентами и
с рациональными коэффициентами и 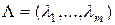 - все его корни из алгебраического замыкания
- все его корни из алгебраического замыкания 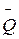 поля
поля 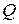 . Рассмотрим множество
. Рассмотрим множество 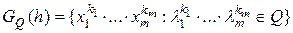
 - множество мономов из поля рациональных выражений
- множество мономов из поля рациональных выражений  (возможно, с отрицательными степенями), которые при подстановке
(возможно, с отрицательными степенями), которые при подстановке 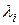 вместо
вместо 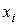 получают рациональные значения. Тогда
получают рациональные значения. Тогда 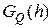 - мультипликативная абелева группа с конечным числом образующих.
- мультипликативная абелева группа с конечным числом образующих.
Доказательство по существу повторяет доказательство предложения 3. Вместо биномов вида  следует рассматривать биномы вида
следует рассматривать биномы вида 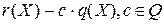 . Более того, вместо поля
. Более того, вместо поля 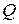 можно рассматривать любую мультипликативную подгруппу
можно рассматривать любую мультипликативную подгруппу 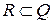 .
.
Следствие 2. Множество всех L-инвариантов оператора 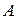 образует поле рациональных выражений.
образует поле рациональных выражений.
Доказательство очевидно. Поле L-инвариантов оператора 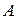 , порожденное элементами
, порожденное элементами 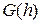 , имеет конечное число образующих – элементов
, имеет конечное число образующих – элементов 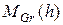 .
.
Проблему описания всех L -инвариантов линейного оператора можно теперь уточнить как проблему построения конечного множества образующих группы 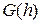 .
.
Определение 3. L-инварианты оператора 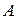 , определенные мультипликативным соотношением между корнями характеристического многочлена
, определенные мультипликативным соотношением между корнями характеристического многочлена 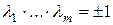 , будем называть целыми. L-инварианты оператора
, будем называть целыми. L-инварианты оператора 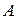 , определенные мультипликативным соотношением
, определенные мультипликативным соотношением  , будем называть рациональными.
, будем называть рациональными.
Предложение 5. Если характеристический многочлена оператора 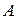 имеет вид
имеет вид  , оператор
, оператор 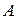 обладает рациональными L-инвариантами.
обладает рациональными L-инвариантами.
Доказательство. Пусть 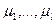 - корни многочлена
- корни многочлена 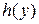 . Тогда
. Тогда  . Каждый из сомножителей вида
. Каждый из сомножителей вида 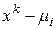 определяет рациональные L-инварианты, которые вычисляются аналогично тому, как это сделано в следствии 2 предложения 2.
определяет рациональные L-инварианты, которые вычисляются аналогично тому, как это сделано в следствии 2 предложения 2.
III. Нелинейные инварианты линейных циклов и собственные полиномы линейных операторов
В общем случае невырожденный линейный оператор 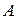 в подходящем базисе может быть представлен матрицей - жордановой формой [12, 13].
в подходящем базисе может быть представлен матрицей - жордановой формой [12, 13].
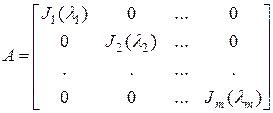 , (4)
, (4)
где 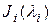 - жордановы клетки разных размеров. Жорданова клетка имеет вид
- жордановы клетки разных размеров. Жорданова клетка имеет вид
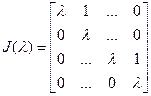 (5)
(5)
Таким образом, теорема 2 относится только к тем строкам матрицы линейного оператора  , которые соответствуют собственным векторам
, которые соответствуют собственным векторам  , т.е. к совокупности последних строк жордановых клеток
, т.е. к совокупности последних строк жордановых клеток  ,
, 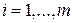 . Ниже мы распространим эту теорему на произвольные невырожденные линейные операторы, введя в рассмотрение жордановы клетки в целом.
. Ниже мы распространим эту теорему на произвольные невырожденные линейные операторы, введя в рассмотрение жордановы клетки в целом.
Для анализа линейных циклов линейный оператор 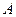 следует рассматривать как линейное преобразование
следует рассматривать как линейное преобразование 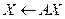 переменных
переменных 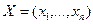 линейного пространства
линейного пространства 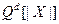 однородных полиномов некоторой степени
однородных полиномов некоторой степени 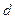 . Преобразование
. Преобразование 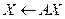 определяет линейное преобразование пространства
определяет линейное преобразование пространства 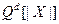 в себя (гомоморфизм)
в себя (гомоморфизм) 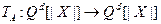 . Для
. Для  оно задано формулой
оно задано формулой
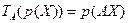 .
.
Определение 3. Полином  называется собственным полиномом линейного оператора
называется собственным полиномом линейного оператора 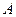 с собственным числом
с собственным числом 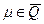 , если
, если 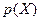 - собственный вектор
- собственный вектор 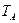 , т.е.
, т.е. 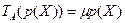 . Таким образом, собственный полином определяется формулой
. Таким образом, собственный полином определяется формулой
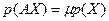 . (6)
. (6)
Замечание 2. Понятия собственного многочлена и L-инварианта линейного оператора – некоторые аналоги понятий основных понятий геометрической теории инвариантов – а именно, понятий относительного и абсолютного инвариантов группы 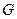 преобразований векторного пространства в том случае, когда эта группа определена как циклическая c образующим элементом
преобразований векторного пространства в том случае, когда эта группа определена как циклическая c образующим элементом 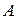 :
: 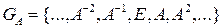 [15].
[15].
Пример 1. Пусть  - собственный вектор оператора
- собственный вектор оператора 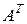 и
и 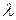 - его собственное значение. Тогда
- его собственное значение. Тогда 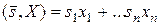 - собственный полином оператора
- собственный полином оператора 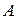 с собственным числом
с собственным числом 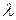 .
.
Предположим, что линейный оператор 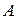 состоит из одной жордановой клетки вида (5), которую обозначим через
состоит из одной жордановой клетки вида (5), которую обозначим через 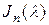 . Если размеры клетки и ее собственное значение в данном контексте не играют роли, их обозначения мы будем игнорировать, обозначая оператор через
. Если размеры клетки и ее собственное значение в данном контексте не играют роли, их обозначения мы будем игнорировать, обозначая оператор через 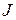 . Приведем решение задачи построения всех собственных полиномов жордановой клетки
. Приведем решение задачи построения всех собственных полиномов жордановой клетки 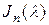 .
.
Теорема. Не существует собственных полиномов от двух переменных 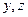 .
.
Доказательство. 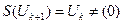 для любого
для любого 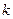 .
.
Рассмотрим однородные многочлены степени  от переменных
от переменных 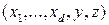 . Пусть
. Пусть 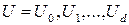 - последовательность подпространств, определенная в (8).
- последовательность подпространств, определенная в (8).
Теорема 3. Существует система многочленов  ,
, 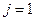 ,
, 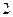 ,…,
,…, 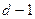 степени
степени 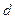 и многочлен
и многочлен 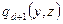 степени
степени  такие, что многочлен
такие, что многочлен
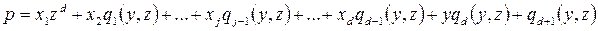 (9)
(9)
является собственным многочленом оператора 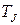 .
.
Пример 2. П оследовательность собственных полиномов жордановой клетки 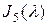 в пространстве
в пространстве 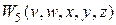 .
.
 ,
, 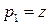 .
.
 ,
, 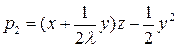 .
.
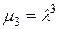 ,
,  .
.
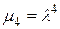 ,
, 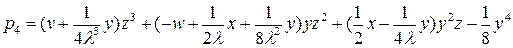 .
.
Теорема 4. Для жордановой клетки 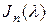 существует набор
существует набор 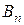 , состоящий из
, состоящий из  собственного полинома вида (9):
собственного полинома вида (9): 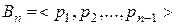 ,
,

 …,
…, 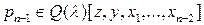 .
.
Любой собственный полином 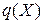 жордановой клетки
жордановой клетки 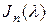 можно представить в виде
можно представить в виде
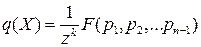 . (15)
. (15)
где 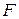 - многочлен от
- многочлен от  переменной с коэффициентами из
переменной с коэффициентами из 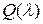 .
.
Замечание 2. Отметим, что формулы (16) по существу определяют изоморфное отображение векторного пространства однородных полиномов степени 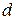
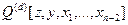 в векторное пространство собственных полиномов
в векторное пространство собственных полиномов 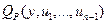 , элементы которого имеют вид
, элементы которого имеют вид  , где
, где 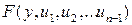 - взвешенно-однородный полином с весами переменных
- взвешенно-однородный полином с весами переменных
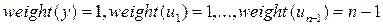 .
.
Система образующих 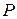 пространства
пространства 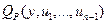 состоит из собственных полиномов и переменной
состоит из собственных полиномов и переменной 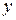 :
:
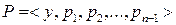 .
.
В системе образующих 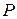 матрица
матрица 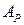 оператора
оператора 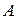 имеет вид
имеет вид
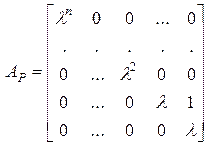 .
.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 509; Нарушение авторских прав?; Мы поможем в написании вашей работы!