Машинные методы синтеза

Практическая проверка вышеупомянутых методов, а также других традиционных алгоритмов синтеза показывает, что вычислительные трудности не позволяют осуществить сквозной синтез регуляторов САУ по единому функционалу качества с учетом возможностей технической реализации и условий эксплуатации САУ. Поэтому предлагается осуществлять синтез изменяемой части САУ в соответствии с процедурой, приведенной на рис. 3.

В таком алгоритме последовательно осуществляется синтез структуры регуляторов САУ U = φ(Y, V, К, t) для линеаризованных матмоделей (ММ), неизменяемых их частей при упрощенном функционале качества I₀=I₀(Y, К, V, t) и минимуме ограничений G₀=G₀(Y, Λ, t)≤N₀ и оптимизация параметров САУ машинно-аналитическим методом уже по полной ММ неизменяемой части Y^*=F(Y, Λ, X, U, t) с учетом дополнительных критериев и ограничений

I₁=I₁(Y,K,V,t), C₁=C₁(Y,Λ,t)≤N₁ (1.23)

учитывающих характеристики процессов S.

Полученные в результате оптимизации искомые параметры регулятора К и V проверяются при моделировании. Алгоритм является итерационным.

В соответствии с представленной на рис. 3 схемой синтеза САУ начальным этапом является синтез линейных регуляторов линейных объектов. Стремление получить первое приближение регуляторов САУ в виде, наиболее близком к синтезируемому в смысле критериев (1.8) и (1.9), и охватить как непрерывные, так и дискретные регуляторы САУ приводит к привлечению алгоритмов методов полиномиальных уравнений (1.16) — (1.19) и частотных характеристик.

Однако в ряде случаев эти алгоритмы оказываются практически неприемлемыми для синтеза многомерных САУ. Этого недостатка лишены методы пространства состояний (МПС). Они представляют собой группу машинных методов синтеза САУ на основе формирования исходной ММ. МПС разработаны в основном для линейных САУ и отличаются от других методов синтеза широкими возможностями по применению ЭВМ для их реализации. В то же время применение МПС для «ручных» расчетов САУ неэффективно.

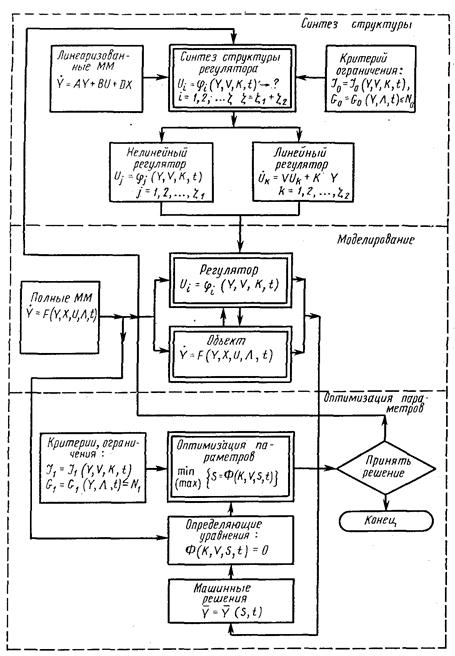
Рис. 3. Схема основного алгоритма синтеза САУ

Создание регулярных методов синтеза на основе представления исходной системы в пространстве состояний еще далеко до завершения, и на сегодняшний день существует лишь ряд способов синтеза линейных управлений линейными объектами.

Рассмотрим основной алгоритм МПС и возможности его применения для синтеза структуры и начальных параметров регуляторов САУ. Применение метода МПС к САУ требует выполнения следующих условий: приводимости исходной линейной системы к форме Коши и исключения минимаксных критериев синтеза и ограничений в (1.8), (1.9).

В предположении, что эти условия выполнены, рассмотрим применение МПС по критерию минимальной длительности процессов к ММ в форме

, (1.24)

получаемой как частный случай из формы Коши. Переходя от этого уравнения к разностному, получим уравнение

(1.25)

где

Следует заметить, что для дискретных систем управления величина Т в (1.25) тождественна периоду дискретности. От ее выбора существенно зависят динамические характеристики синтезированной системы, требования, предъявляемые к цифровому вычислителю и исполнительному элементу.

Существует ряд способов вычислений матриц Ф₀(Т),Ф₁(Т),Ф₂(Т), из которых наиболее эффективно их вычисление с помощью метода Ракитского на основе рекуррентных формул. Основной трудностью при этом является зависимость сходимости вычислительного процесса от величины шага Т, обусловленности и размерности матриц А, В, D. Если в качестве критерия синтеза принять минимальное время перехода системы из начального положения Y[0] в положение Y[NT] при X(t)=0, то минимальное N определяется из известного соотношения

N ≥ m/ l (1.26)

где m — порядок исходной системы (1.24), а l — размерность вектора U(nT). Искомое управление U(nT) находят из уравнения

, (1.27)

которое получается в результате решения системы уравнений

(1.28)

относительно вектора

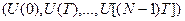
Система (1.28) получается из (1.27) при и в предположении, что известна полная информация о выходных координатах системы Y(nT). Тогда все дело сводится к нахождению матрицы σ(Т). Имея в виду критерии качества систем регулирования, положим в (1.28) Y(NT)=0, тогда σ(Т) будет содержать первые l строк матрицы

(1.29)

которая должна быть неособой — |S(T)|=0.

Если l — размерность вектора U, то общее число дискретных управлений (импульсов, поступающих на исполнительный элемент) будет k=N l, где N — число необходимых шагов для перевода системы из состояния Y[0] в состояние Y[NT]. Недостатками МПС являются сравнительная сложность (при увеличении размерности системы) вычислительной процедуры и лишь частичное отражение критериев (1.8) — (1.9) в критериях метода.

В тех случаях, когда для синтеза структуры САУ линейные управления оказываются недостаточными для решения задач, поставленных перед САУ, приходится осуществлять синтез нелинейных регуляторов. В частности, в предыдущих методах не учитывается ограничение исполнительных устройств управления. Управления, построенные с их учетом, основаны на замечательной теореме выдающегося советского математика Л. С. Понтрягина, получившей название принципа максимума.

В соответствии с принципом максимума для динамической системы (1.24) с функционалом общего вида

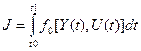(1.30)

разработан ряд методов синтеза управления U(t), переводящих систему из точки Y(t₀) в точку Y(t_n) таким образом, что функционал (1.30) принимает наименьшее значение, а

|U(t)|≤U_ДОП. (1.31)

Так как «строгий» синтез оптимального управления U(t) при условиях и ограничениях, принимаемых в проектировании САУ, не имеет практического приложения, то для машинной ориентации целесообразно воспользоваться квазиоптимальными методами синтеза нелинейных регуляторов. Достаточно эффективной оказывается машинная ориентация предложенного Л. Е. Конаревым метода последовательного синтеза управлений, оптимальных по быстродействию. Этот метод позволяет получать управление в ряде САУ, удовлетворяющее критериям (1.8), (1.9).

Дата добавления: 2014-01-20