Интенсивность испарения влаги

Скорость сушки определяет один из важнейших технологических параметров – интенсивность испарения влаги из материала m, которая выражается количеством влаги, испаряемой с единицы поверхности материала F в единицу времени:

,

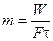где τ − общая продолжительность сушки.

Интенсивность испарения влаги связана с механизмом тепло- и массообмена влажного материала с окружающей средой. Как отмечалось, этот механизм является достаточно сложным, так как включает процессы перемещения влаги из глубины материала к его поверхности и перемещения влаги (в виде пара) с поверхности материала в окружающую среду. Каж­дый из этих процессов подчиняется собственным закономерностям и протекает с различной интенсивностью в разные периоды сушки.

1.9. Испарение влаги с поверхности материала [1, 5]

Этот процесс происходит главным образом вследствие диффузии пара через пограничный слой воз­духа у поверхности материала (внешняя диффузия). Таким путем осуществляется перенос до 90% всей влаги; он обусловливается движущей силой — разностью концентраций или разностью парциальных давлений пара у поверхности материала р _м и в окружающей среде р _п. Помимо диффузионного потока перенос некоторого количества влаги и теплоты происходит за счет движения молекул пара в пограничном слое (мольный перенос). Наконец, перепад температур в пограничном слое также ускоряет перемещение молекул пара (термодиффузия). В условиях конвективной сушки, при относительно низких температурах, перенос влаги за счет термодиффузии пренебрежимо мал.

В период постоянной скорости влажность материала больше гигроскопической, пар у его поверхности является насыщенным (р _м = р _п) и соответствует температуре мокрого термометра t _м. В этот период происходит интенсивное поступление влаги из внутренних слоев материала к его поверхности. Скорость поверхностного испарения влаги из материала может быть принята равной скорости испарения ее со свободной поверхности жидкости и определена, согласно закону Дальтона. Поэтому урав­нение влагоотдачи с поверхности материала имеет вид

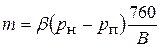, (1.47)

где β – коэффициент массоотдачи (влагоотдачи).

В уравнении парциальные давления пара р _н и р _п, а также барометрическое давление В выражены в мм рт. ст.

Выражая коэффициент массоотдачи через диффузионный критерий
Нуссельта, представим уравнение в форме

.

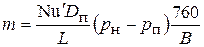В этом уравнении D _п – коэффициент влагопроводности (для влаги, находящейся в парообразном состоянии); D _п – аналог коэффициента теплопроводности (находится опытным путем); L – определяющий геометрический размер по направлению движения воздуха вдоль поверхности испарения влаги из материала.

Трудность практического использования уравнений заключается в том, что β и соответственно Nu’ зависят не толь­ко от основного фактора — скорости воздуха (газа), но и от многих дру­гих: условий обтекания сушильным агентом поверхности материала, ее формы и размеров, температуры сушки и т.п.

Имеется ряд эмпирических зависимостей, с помощью которых можно в первом приближении рассчитать величину β.

Дата добавления: 2014-01-20