
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Малая выборка
|
|
|
|
Под малой выборкой понимается несплошное обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности.
(n<30, может доходить до 4-5). Средняя ошибка малой выборки вычисляется по формуле:
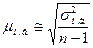 , где
, где 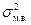 - дисперсия малой выборки;
- дисперсия малой выборки; 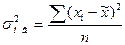
Предельная ошибка малой выборки 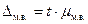
где t - коэффициента доверия, определяемый по закону распределения Стьюдента (1908 г. английским математиком У. Госсетом), в зависимости от уровня значимости 0,05 или 0,01 и численности выборки n.
Графически распределение Стьюдента имеет вид одновершинной кривой, которая симметрична относительно оси ординат и при увеличении объема выборки приближается к кривой нормального распределения.
При проведении малой выборки для определения предельной ошибки выборки используются следующие показания распределения Стьюдента.
| n | t | |
| 0,05 | 0,01 | |
| 3,183 | 5,841 | |
| 2,777 | 4,604 | |
| 2,571 | 4,032 | |
| 2,447 | 3,707 | |
| 2,364 | 3,500 | |
| 2,307 | 3,3546 | |
| 2,263 | 3,250 | |
| 2,119 | 2,910 | |
| 2,08 | 2,832 | |
| 2,056 | 2,779 | |
| 2,042 | 2,75 |
При контрольной проверке качества поставленного в торговлю товара получены следующие данные о содержании влаги в пробах, %. По данным выборочного обследования необходимо установить с вероятностью 0,95, предел в котором находится средний процент содержания воды в данной партии товара.
| Пробы xi | 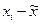
| (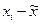 )2 )2
| Пробы xi | 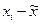
| (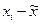 )2 )2
|
| 4,3 | 0,2 | 0,04 | 3,9 | -0,2 | 0,04 |
| 4,2 | 0,1 | 0,01 | 4,5 | 0,4 | 0,16 |
| 3,8 | 0,3 | 0,09 | 4,4 | 0,3 | 0,09 |
| 4,3 | 0,2 | 0,04 | 4,0 | -0,1 | 0,01 |
| 3,7 | -0,4 | 0,16 | 3,9 | -0,2 | 0,04 |
| Итого 41,0 | - | 0,68 |
Находим среднюю пробу малой выборки 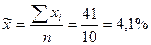
Далее определим дисперсию малой выборки 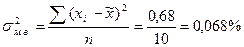
Средняя ошибка малой выборки равна 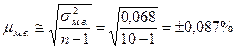
При n=10 и заданном уровне значимости a=0,05 находим по таблице коэффициент доверия t = 2,263. Предельная ошибка малой выборки составит: 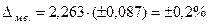
Следовательно, с вероятностью 0,95 можно утверждать, что во всей партии товара содержание воды находится в пределах:
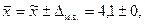 2 т. е. в пределах от 3,9% до 4,3%.
2 т. е. в пределах от 3,9% до 4,3%.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 393; Нарушение авторских прав?; Мы поможем в написании вашей работы!