Показатели тесноты связи множественной корреляции

Теснота связи между изучаемыми показателями при множественной корреляции определяется на основе различных коэффициентов:

парные коэффициенты корреляции r измеряют тесноту линейной связи между факторами и между результативным признаком и каждым из рассматриваемых факторов без учета их взаимодействия с другими факторами;

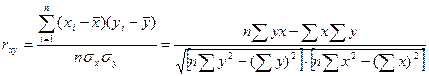
частные коэффициенты корреляции характеризуют степень влияния факторов на результативный признак при условии, что остальные факторы присутствуют, но закреплены на постоянном уровне. В зависимости от количества факторов, влияние которых исключается, частные коэффициенты корреляции могут быть первого порядка (при исключении влияния одного фактора), второго порядка (при исключении влияния двух факторов) и т.д. Частный коэффициент корреляции первого порядка между у и x₁ при исключении влияния x₂ в двухфакторной модели рассчитывается по формуле

;

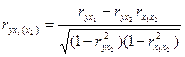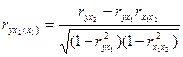
где , , 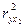— парные коэффициенты корреляции между соответствующими признаками;

совокупный коэффициент множественной корреляции R оценивает тесноту связи между результативным признаком и всеми факторами. Это основной показатель линейной множественной корреляции. Для двухфакторной модели совокупный коэффициент множественной корреляции рассчитывается по формуле:

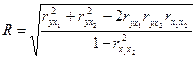
Совокупный коэффициент корреляции Rизменяется от 0 до 1. Чем меньше эмпирические значения результативного признака отличаются от выровненных по линии множественной регрессии, тем корреляционная связь между исследуемыми показателями теснее и совокупный коэффициент множественной корреляции ближе к единице. Совокупный коэффициент множественной детерминации, равный R², показывает, какая часть вариации результативного признака обусловлена влиянием факторов, включенных в модель.

Проверка значимости коэффициента множественной корреляции осуществляется на основе F-критерия Фишера.

Гипотеза о значимости коэффициента множественной корреляции подтверждается, если F_расч>F_кр (при соответствующем уровне значимости 1% или 5% и числе степеней свободы n₁ =2 –число степеней свободы числителя и n₂=n-3- число степеней свободы знаменателя).

Совокупный индекс множественной корреляции характеризует тесноту связи между результативным признаком и всеми факторами при криволинейной зависимости:

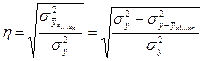
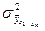- дисперсия результативного признака под влиянием факторов, включенных в модель;

-остаточная дисперсия результативного признака, вызванная влиянием не учтенных моделью факторов. При линейной форме связи совокупный коэффициент и индекс множественной корреляции равны между собой.

Взаимосвязи между признаками анализируются на материале выборочных наблюдений. Поэтому для проверки того, что полученные зависимости носят закономерный, а не случайный характер, оценивается значимость показателей корреляции и регрессии с помощью критериев t-Стьюдента и F-Фишера.

Корреляционно-регрессионный анализ служит для оценки показателей бизнес-плана и нормативных экономических показателей. Дает возможность для краткосрочного прогнозирования развития производства предприятий. Уравнение множественной регрессии позволяет найти теоретическое, возможное значение результативного показателя при определенных значениях факторных признаков. Задаваясь средними или лучшими значениями факторов по совокупности предприятий, можно установить потенциально возможный уровень результативного показателя, что раскрывает резервы предприятия по улучшению экономической деятельности.

РЯДЫ ДИНАМИКИ

Вы знаете, что любое явление или процесс находятся в постоянном развитии во времени.

Статистика изучает социально-экономические явления и процессы, находящиеся в непрерывном движении, изменении, развитии, т.е. в динамике

. Ряд динамики - это расположенные в хронологической последовательности числовые значения показателей, которые характеризуют изменение явления во времени.

Каждый временной ряд состоит из двух элементов: 1) момента или периода времени, к которым относятся статистические данные; 2) из уровней ряда – это статистические показатели, которые характеризуют изучаемый объект за указанный период времени.

Ряды динамики обычно представляются в виде таблиц или графически. Наиболее распространенным видом является линейная диаграмма, которая строится в прямоугольной системе координат. На оси абсцисс откладывается время, а на оси ординат – уровня ряда. Также используются столбиковая диаграмма, секторная диаграмма и др.

Виды рядов динамики:

1) по виду показателей выделяют ряды из абсолютных (временной ряд объема выпуска продукции предприятием в стоимостном выражении, временной ряд числа выпускников ВУЗа; средних (средними величинами могут выражаться уровни, характеризующие динамику средней заработной платы на предприятиях, среднесписочной численностью работников предприятия)и относительными величинами (ОПРП, динамика доли городского и сельского населения, динамика доли произведенной промышленной и сельскохозяйственной продукции.)

2) по времени, отраженному в динамических рядах. Делятся на моментные (характеризуют состояние явления на определенную дату например, численность студентов факультета ЭиП на конец года.

Поскольку в каждом последовательном уровне содержится полностью или частично значение предыдущего уровня, то суммировать уровни моментного ряда не следует, т.к. это приводит к повторному счету.)

Интервальным рядом называется ряд динамики, уровни которого характеризуют размер явления за конкретный период времени (год, квартал, месяц и т.д.) Например, данные динамики о добычи нефти в России. Значения уровней интервального ряда из абсолютных показателей можно суммировать, что позволяет получить ряды динамики более укрупненных периодов или дробить, чтобы получить среднемесячные данные.

Добыча нефти в РФ, млн. тонн

3) по расстоянию между датами подразделяются на ряды с равноотстоящими интервалами (расстояние между датами регистрации или окончания интервалов одинаково) с неравноотстоящими (расстояние между датами регистрации или окончания интервалов различно) Например, ряд динамики численности населения (промежуток в начале составляет 10 лет, а в конце 1 год).

4) по числу показателей ряды динамики делят на:

-изолированные ряды, содержащие только один показатель;

-комплексные ряды, содержащие несколько взаимосвязанных показателей;

Основное требование, предъявляемое к динамическим рядам, - сопоставимость их уровней. Чтобы быть сопоставленными, уровни ряда должны иметь:

1) одни и те же содержательные границы;

2) одни и те же территориальные границы;

3) одни и те же единицы измерения (если показатели приводятся в ценностных единицах, то необходимо перевести его в другие единицы (т.к. со временем происходит непрерывное изменение цен), а если это невозможно, то представить его в виде относительного показателя, например, имеется ряд динамики размера реальной среднемесячной заработной платы 1995 и 1999 г.г., то чтобы сопоставить эти два ряда, необходимо их привести к уровню потребительских цен за этот же период путем деления размера заработной платы на уровень потребительской цены и умножить на 100%, тогда возможно сопоставление этих рядов).

4) одинаковую продолжительность периодов, за которые приводятся данные (для интервальных рядов);

5) единую методологию расчета.

Ряды динамики могут быть представлены графически. Наиболее распространенным видом является линейная диаграмма, которая строится в прямоугольной системе координат. На оси абсцисс откладывается время, а на оси ординат – уровня ряда. Также используются столбиковая диаграмма, секторная диаграмма и др.

Дата добавления: 2014-01-20