Средние характеристики ряда динамики

Для обобщающей характеристики динамики исследуемого явления определяют средние показатели динамики — средний уровень ряда и средние показатели изменения уровней ряда.

Метод расчета среднего уровня ряда динамики зависит от вида временного ряда.

Для интервального ряда с равными промежутками времени средний уровень рассчитывается по формуле простого среднего арифметического:

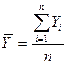
где n-число уровней ряда

Для интервального ряда с неравными промежутками времени средний уровень рассчитывается по формуле среднего арифметического взвешенного:

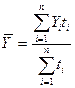
где где t_i-число периодов времени, в течение которых уровень не изменялся.;

y_1,,y₂, y_n-уровни ряда.

Средний уровень моментного ряда определяется по формуле среднего хронологического. Для моментных рядов с равноотстоящими уровнями средний уровень моментного ряда будет равен простому среднему хронологическому:

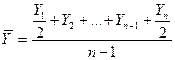
где n-число дат

y_1,,y₂, y_n-уровни ряда в последовательные моменты времени.

Средний уровень моментного ряда с неравноотстоящими уровнями определяется по формуле среднего хронологического взвешенного с весами t_i, равными продолжительности промежутков времени между моментами, в которые происходят изменения в уровнях динамического ряда:

,

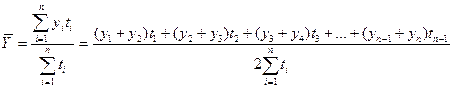где t_i-количество дней (месяцев) между смежными датами.

Например, на 1 января отчетного года стоимость основных средств предприятий составляла 75 млрд. руб. В марте были приобретены основные средства на сумму 2 млрд. руб., в мае выбыло основных средств на 7 млрд. руб., а в сентябре было приобретено еще основных средств на 8 млрд. руб. Определим среднюю годовую стоимость основных средств предприятия. Для удобства расчетов данные представим в виде табл. 8.5.

Среднегодовая стоимость основных средств предприятия по данным приводимого примера составит 74,417 млрд. руб.:

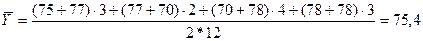млрд. руб.

Если же ориентироваться на стоимость основных средств предприятия на начало и конец отчетного года, т.е., например, использовать показатели балансового отчета предприятия, то полу­чим иной показатель среднегодовой стоимости основных средств предприятия:

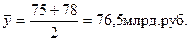
где 78 млрд. руб. – стоимость основных средств на конец года (78=75+2-7+8 по условию).

Даты времени	Стоимость основных средств (в млрд. руб.)	Число месяцев, в течение которых стоимость не изменялась	yiti
I/I		-
I/IV
I/VI
I/X
I/I тек
Итого	-

Поэтому для анализа деятельности предприятия следует пользоваться данными внутренней отчетности, что позволяет получить более достоверную оценку результатов.

Однако нужно иметь в виду, что средняя будет достаточно надежной характеристикой ряда динамики, если она характеризует период со стабильными уровнями развития. Если за исследуемый период можно выделить этапы, в течение которых условия развития существенно менялись, то пользоваться общей средней не целесообразно, а предпочтение нужно отдать средним, рассчитанным по отдельным этапам.

Средние показатели изменения уровней ряда рассчитываются усреднением цепных показателей динамики.

1 Средний абсолютный прирост (убыль) рассчитывается как простая средняя арифметическая из показателей абсолютных цепных приростов:

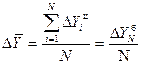
Значение среднего абсолютного прироста показывает, насколько в среднем изменяется уровень ряда за единичный промежуток времени.

Средний относительный прирост (коэффициент роста) вычисляется по формуле среднего геометрического из показателей цепных коэффициентов роста и показывает, во сколько раз в среднем изменяется уровень ряда за единичный промежуток времени:

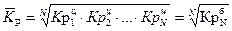
3. Средний темп роста представляет собой средний относительный прирост (коэффициент роста), выраженный в процентах:

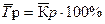
4. Средний темп прироста, показывает, на сколько процентов в среднем за единичный промежуток времени изменяется уровень ряда. Рассчитывается он на основе среднего темпа роста, вычитанием из последнего 100%:

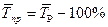
Если уровни ряда динамики снижаются, то средний темп роста будет меньше 100%, а средний темп прироста будет отрицательной величиной.

Дата добавления: 2014-01-20