Автокорреляция в остатках

Рассматривая последовательность остатков как временной ряд, можно построить график их зависимости от времени. В со­ответствии с предпосылками МНК остатки ε _t должны быть слу­чайными (рис. 1 а). Однако при моделировании временных ря­дов нередко встречается ситуация, когда остатки содержат тен­денцию (рис. 1 б) и в))или циклические колебания (рис.1 г)). Это свидетельствует о том, что каждое следующее значение ос­татков зависит от предшествующих. В этом случае говорят о на­личии автокорреляции остатков.

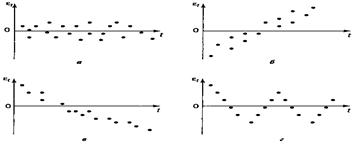
Рис. 1. Модели зависимости остатков от времени

а— случайные остатки; б — возрастающая тенденция в остатках;

в - убывающая тенденция в остатках;

г - циклические колебания в остатках

Существуют два наиболее распространенных метода опреде­ления автокорреляции остатков. Первый метод - это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции. Второй метод — использо­вание критерия Дарбина — Уотсона и расчет величины

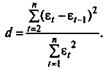
Соотношение между критерием Дарбина — Уотсона и коэф­фициентом автокорреляции остатков первого порядка:

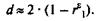
Таким образом, если в остатках существует полная положи­тельная автокорреляция и= 1, то d = 0. Если в остатках полная отрицательная автокорреляция, то= -1 и, следовательно, d = 4. Если автокорреляция остатков отсутствует, то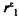= 0 и d = 2. Следовательно,

0 ≤ d ≤ 4.

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина - Уотсона следующий. Выдвигается гипотеза H₀ об отсутствии автокорреляции остатков. Альтернативные ги­потезы Н₁ и H* ₁ состоят, соответственно, в наличии положитель­ной или отрицательной автокорреляции в остатках. Далее по спе­циальным таблицам (см. приложение) определяются критичес­кие значения критерия Дарбина - Уотсона d_L и d_U для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости α. По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Принятие или отклонение каж­дой из гипотез с вероятностью (1 — α) рассматривается на рис. 2.

Рис. 2. Механизм проверки гипотезы о наличии автокорреляции остатков

Если фактическое значение критерия Дарбина — Уотсона по­падает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу H ₀.

Есть несколько существенных ограничений на применение критерия Дарбина — Уотсона.

Во-первых, он неприменим к моделям, включающим в качест­ве независимых переменных лаговые значения результативного признака, т. е. к моделям авторегрессии. Для тестирования на ав­токорреляцию остатков моделей авторегрессии используется критерий h Дарбина.

Во-вторых, методика расчета и использования критерия Дар­бина — Уотсона направлена только на выявление автокорреляции остатков первого порядка. При проверке остатков на автокорре­ляцию более высоких порядков следует применять другие методы, рассмотрение которых выходит за рамки данного учебника.

В-третьих, критерий Дарбина — Уотсона дает достоверные результаты только для больших выборок. В этом смысле резуль­таты примера 6.4 нельзя считать достоверными ввиду чрезвычай­но малого числа наблюдений n = 7, по которым построена модель регрессии.

Дата добавления: 2014-01-20