Плоский математический маятник

III. Вязкое трение.

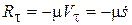(11.15)

Такая модель трения применяется, когда между трущимися поверхностями присутствует смазка.

Система уравнений движения точки в этом случае имеет вид:

(11.16)

Уравнения (11.16) решаются в той же последовательности, что и уравнения (11.8).

Рассмотрим пример на несвободное движение материальной точки, когда она удерживается на линии.

Математическим маятником называется материальная точка, подвешенная на нерастяжимой нити, совершающая движение в одной вертикальной плоскости под действием силы тяжести.

Рассмотрим движение маятника массой m и длиной нити ОМ = l (рис.11.4) в вертикальной плоскости Oxy, используя оси естественного

Рис.11.4

трехгранника М 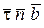. Пусть О ₁ – начало отсчёта дуги s, определяющей положение материальной точки М на траектории, а М ₀ – её начальное положение (необязательно совпадает с началом отсчёта), определяемое дугой s ₀. 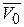- начальная скорость точки. Освободимся от связи и заменим действие нити реакцией нити , направленной вдоль нити к точке подвеса О. Тогда материальная точка будет двигаться под действием двух сил:

силы тяжести 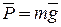и реакции нити . Основной закон динамики будет иметь вид

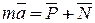(11.17)

Проектируя (11.17) на естественные оси получим дифференциальные уравнения движения точки в форме Эйлера:

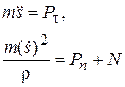(11.18)

В уравнениях (11.18) перейдём к новой более удобной при движении точки по дуге окружности переменной – углу , образованным нитью с осью Оx (рис.11.4): .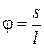

Тогда в уравнениях (11.18)

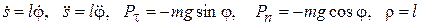(11.19)

и, следовательно, после преобразований получим:

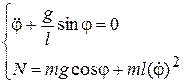(11.20)

При решении обратной задачи несвободной точки первое уравнение системы (11.20) определяет закон движения точки, второе – реакцию нити. Первое уравнение представляет собой нелинейное дифференциальное уравнение, которое не интегрируется в элементарных функциях.

Рассмотрим случай малых колебаний маятника, положив 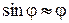и обозначив .

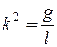В этом случае дифференциальное уравнение движения маятника примет вид:

. (11.21)

Уравнение (11.21) является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.

Характеристическое уравнение этого дифференциального уравнения имеет вид:

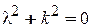. (11.22)

Так как его корнями являются мнимые числа 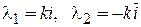, то общее решение дифференциального уравнения можно представить в виде:

.

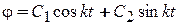Константы интегрирования С ₁ и С ₂ определим из начальных условий:

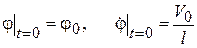. (11.23)

Так как

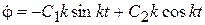, (11.24)

то подставляя начальные условия (11.23) в решение (20.6) и (20.8), получим

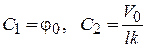
и, следовательно,

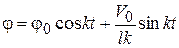(11.25)

Преобразуем решение (11.25), умножив и разделив правую часть на выражение :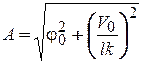

.

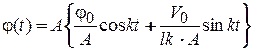Так как , обозначим .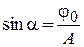

Тогда 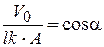и, следовательно,

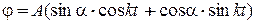или

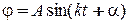(11.26)

Получили, что материальная точка совершает движение по синусоидальному закону. Такое движение точки называется гармоническими колебаниями. Характеристиками такого движения являются:

А – амплитуда колебаний;

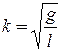- круговая частота колебаний;

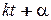- фаза колебаний;

- начальная фаза колебаний;

Т - период колебаний (время в секундах, за которое фаза колебаний изменится на 2p):

.

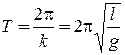Таким образом, малые колебания математического маятника будут гармоническими колебаниями с частотой колебаний 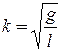и периодом малых колебаний 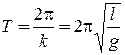. Они будут также изохронными, т.к. период колебаний не зависит от начальных условий.

Подставляя решение (11.26) во второе уравнение системы (11.20) определим силу натяжения нити N.

Дата добавления: 2014-01-20