
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Работа силы на элементарном и конечном перемещениях
|
|
|
|
Элементарная работа силы D А равна скалярному произведению векторов силы  и элементарного перемещения
и элементарного перемещения 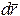 :
:
D А =  ×
× 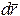 .
.
Вектор элементарного перемещения 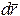 направляется по касательной к траектории в данной точке (рис. 14.2) и по модулю равен элементарной дуге ds. Исходя из определения скалярного произведения векторов, элементарную работу можно вычислить по следующим формулам:
направляется по касательной к траектории в данной точке (рис. 14.2) и по модулю равен элементарной дуге ds. Исходя из определения скалярного произведения векторов, элементарную работу можно вычислить по следующим формулам:
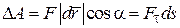 или
или  , (14.7)
, (14.7)
где 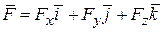 ,
, 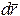 = dx
= dx 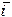 + dy
+ dy 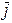 + dz
+ dz  .
.
При этом знак элементарной работы будет положительным, если угол a острый. Если угол a тупой, то элементарная работа будет отрицательной.
Работа силы на конечном перемещении 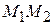 (рис. 14.2) равна криволинейному интегралу, взятому вдоль дуги кривой от
(рис. 14.2) равна криволинейному интегралу, взятому вдоль дуги кривой от 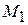 до
до  , от элементарной работы:
, от элементарной работы:
 . (14.8)
. (14.8)
Знак работы имеет следующий смысл: если сила способствует движению, то работа положительна, если не способствует движению - отрицательна. Единицей измерения работы в системе СИ является
1 джоуль (Дж) = 1 Н× м = 1 кг ×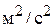 .
.
 |
Рис. 14.2
Примеры работы сил, наиболее часто используемые в задачах:
1). Работа сил тяжести:
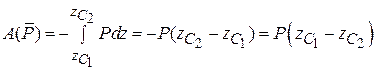 .
.
При перемещении абсолютно твердого тела из положения с центром масс в точке  (рис. 14.3) в положение с центром масс в точке
(рис. 14.3) в положение с центром масс в точке 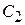 работа силы тяжести тела равна произведению веса тела на вертикальное перемещение его центра масс. В случае перемещения твердого тела из положения с центром масс в точке C 2 в положение с центром масс в точке C 1 работа силы тяжести поменяет знак:
работа силы тяжести тела равна произведению веса тела на вертикальное перемещение его центра масс. В случае перемещения твердого тела из положения с центром масс в точке C 2 в положение с центром масс в точке C 1 работа силы тяжести поменяет знак:
 = ± Ph, (14.9)
= ± Ph, (14.9)
 где
где  .
.
Рис. 14.3
2). Работа силы трения скольжения. Величина силы трения, действующей на материальную точку М при ее движении по шероховатой поверхности (рис. 14.4), определяется по формуле Кулона-Амонтона  , где f – коэффициент трения, N – величина нормальной реакции поверхности.
, где f – коэффициент трения, N – величина нормальной реакции поверхности.
Тогда по формуле (25.8)
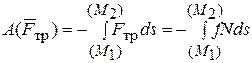 .
.
Если величина силы трения постоянная, то
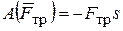 , (14.10)
, (14.10)
где 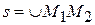 .
.

Рис. 14.4
3). Работа силы, приложенной к вращающемуся телу.
При вращательном движении, так как 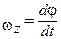 и
и 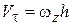 элементарная работа силы
элементарная работа силы  , приложенной к твердому телу, вращающемуся вокруг неподвижной оси, равна
, приложенной к твердому телу, вращающемуся вокруг неподвижной оси, равна
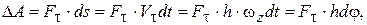
где h –расстояние от точки приложения силы до оси вращения.
Следовательно,
 (14.11)
(14.11)
где  – момент силы
– момент силы  относительно оси вращения z,
относительно оси вращения z, 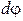 – элементарное угловое перемещение тела.
– элементарное угловое перемещение тела.
Работа силы  на конечном угле поворота
на конечном угле поворота 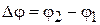 , где
, где  и
и 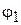 – конечное и начальное значения угла j, определяющего положение тела, вычисляется по формуле
– конечное и начальное значения угла j, определяющего положение тела, вычисляется по формуле
 ,
,
где 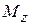 - момент силы
- момент силы  относительно оси вращения z.
относительно оси вращения z.
В случае постоянного момента
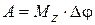 .
.
4). Работа внутренних сил твердого тела. Сумма работ всех внутренних сил  абсолютно твердого тела на любом его перемещении равна нулю.
абсолютно твердого тела на любом его перемещении равна нулю.
Утверждение доказывается на основании теоремы кинематики о проекциях скоростей двух точек тела и того, что исходя из аксиомы А3, внутренние силы входят в систему попарно, являясь противоравными силами.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1378; Нарушение авторских прав?; Мы поможем в написании вашей работы!