
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение реакций опор вращающегося тела
|
|
|
|
Рис.15.3 | Пусть твердое тело вращается вокруг неподвижной оси z под действием приложенных к нему внешних активных сил 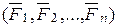 и реакции связей и реакции связей  и и 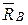 , приложенных в закрепленных точках тела А и В. Определим реакции связей , приложенных в закрепленных точках тела А и В. Определим реакции связей  и и 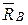 , как величины, зависящие от приложенных сил и характера вращения тела. Примем точку А за начало координат и разложим реакции связей на составляющие , как величины, зависящие от приложенных сил и характера вращения тела. Примем точку А за начало координат и разложим реакции связей на составляющие
|
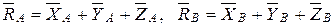 .
.
Пусть  - угловая скорость тела,
- угловая скорость тела, 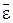 - угловое ускорение тела,
- угловое ускорение тела,  - центр масс тела, АВ = l.
- центр масс тела, АВ = l.
Применим теорему об изменении количества движения:
 .
.
В проекциях на оси координат получим:
 (15.8)
(15.8)
Применяя теорему об изменении кинетического момента относительно точки А, имеем
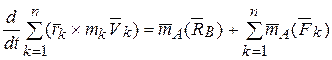 (15.9)
(15.9)
Определим проекции векторных произведений в равенстве (26.9):

Тогда векторное уравнение (15.6) в проекциях на оси координат запишется в следующем виде:
 (15.10)
(15.10)
Выразим в уравнениях (15.8) и (15.10) все производные от координат через угловую скорость и угловое ускорение тела. Для этого введём цилиндрические координаты. Декартовы координаты связаны с цилиндрическими координатами 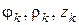 (рис.26.3) формулами
(рис.26.3) формулами
 (15.11)
(15.11)
Вычислим производные, учитывая, что при вращательном движении тела изменяется только угловая координата k -ой точки тела Mk:
 (15.12)
(15.12)
Выполняя операции дифференцирования и подставляя значения производных  в (15.8) получим:
в (15.8) получим:
 (15.13)
(15.13)
Выполняя операции дифференцирования в (15.10) и подставляя значения производных (15.13), после сокращений получим:
 (15.14)
(15.14)
В формулах (15.13) и (15.14) вынося квадрат угловой скорости и угловое ускорение за знак суммирования и обозначая осевой момент инерции 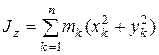 , центробежные моменты инерции
, центробежные моменты инерции  , координаты центра масс
, координаты центра масс 
 , получим окончательно систему уравнений:
, получим окончательно систему уравнений:
|

Последнее уравнение системы (15.15) не содержит реакций. Оно является уравнением вращательного движения тела, из которого находятся угловое ускорение  и угловая скорость
и угловая скорость  . Остальные пять уравнений содержат шесть неизвестных реакций. Следовательно, система является неопределённой. Из третьего уравнения можно определить лишь сумму реакций
. Остальные пять уравнений содержат шесть неизвестных реакций. Следовательно, система является неопределённой. Из третьего уравнения можно определить лишь сумму реакций 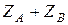 . Эта неопределённость устраняется конструктивно заменой верхней сферической опоры в точке В цилиндрической. Это дает последней свободу перемещения вдоль оси z и тогда
. Эта неопределённость устраняется конструктивно заменой верхней сферической опоры в точке В цилиндрической. Это дает последней свободу перемещения вдоль оси z и тогда 
Из системы уравнений (15.15) видно, что реакции опор зависят как от внешних активных сил, так и от кинематических характеристик тела, координат центра масс  и центробежных моментов инерции тела
и центробежных моментов инерции тела  . Составляющие реакций, зависящие от последних, называются динамическими. Составляющие реакций, зависящие только от внешних активных сил, называются статическими. При быстром вращении тела динамические составляющие реакций могут быть большими. Определим условия, при которых динамические составляющие равны нулю.
. Составляющие реакций, зависящие от последних, называются динамическими. Составляющие реакций, зависящие только от внешних активных сил, называются статическими. При быстром вращении тела динамические составляющие реакций могут быть большими. Определим условия, при которых динамические составляющие равны нулю.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 672; Нарушение авторских прав?; Мы поможем в написании вашей работы!
