Основные понятия аналитической механики

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ

ЛЕКЦИЯ 16

На прошлой лекции мы закончили изучение общих теорем динамики и их применение в динамике твердого тела. В некоторых случаях общие теоремы динамики позволяют до конца решить задачу определения движения механической системы. В тех случаях, когда нет необходимости знать движение каждой материальной точки, теоремы позволяют определить изменение таких общих характеристик, как количество движения, кинетический момент, кинетическая энергия, центр масс.

Однако в случаях несвободных систем, приходится при этом вводить неизвестные реакции связи, определение которых не всегда требуется по условиям задачи и определение которых, к тому же, бывает затруднительно, или вовсе невозможно.

Раздел теоретической механики, называемый аналитической механикой,изучает общие методы, позволяющие составлять дифференциальные уравнения движения несвободных механических систем, не вводя реакции идеальных связей.

Связи и их классификация

При изучении динамики несвободной материальной точки мы уже рассматривали связи. Обобщим эти понятия на систему материальных точек.

Механическая система называется свободной, если ее точки могут занимать любые положения, а их скорости могут принимать произвольные значения. В противном случае механическая система называется несвободной. Для несвободных систем должны быть указаны ограничения, накладываемые на координаты или скорости или на те и другие. Эти ограничения, как мы знаем, называются связями. Они могут быть записаны в виде уравнений или неравенств.

В общем случае уравнение связи можно записать в виде:

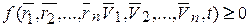или

(16.1)

Если в соотношении (16.1) реализуется только знак равенства, то связь называется удерживающей, если в виде неравенства, то – неудерживающей. Если уравнение связи не содержит скорости точек, т.е.

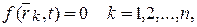то (16.2)

связь называется геометрической или голономной.

Если же в уравнение связи входят скорости точек, то связь называется кинематической или дифференциальной. Если уравнение кинематической связи нельзя проинтегрировать и нельзя представить в виде (16.2), то такая связь называется неголономной.

Пример 1. Гантель (рис. 16.1).

Две материальные точки связанные невесомым стержнем называются «гантелью». Пусть длина стержня равна l.

Рис. 16.1

Тогда координаты материальных точек удовлетворяют уравнению геометрической связи:

Пример 2. Кривошипно-ползунный механизм (рис. 16.2).

Рис.16.2

Рассмотрим механизм как систему связанных материальных точек А и В. Уравнения связей:

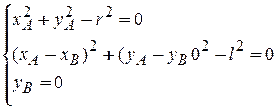
Дата добавления: 2014-01-20