Практические аспекты использования теоремы отсчетов и выбора частоты дискретизации

Восстановление аналогового сигнала

Из анализа рис. 1.15, г, вытекает правило восстановления аналогового сигнала: используя фильтр нижних частот, необходимо избавиться от спектральных составляющих с частотой выше f_m. При этом фильтр должен быть настроен так, чтобы ослабление при f_m отсутствовало, а на частоте f₀ - f_m было бы бесконечно большим.

Из изложенного выше можно сделать следующий вывод: исходную функцию можно восстановить с помощью выборочных значений непрерывной, ограниченной по полосе временной функции, если выполняется условие f₀ > 2f_m. Для этого необходимо образовать из выбранных значений последовательность импульсов Дирака и подать их на вход идеального фильтра нижних частот с f_гр = f_m.

Если частоту выборки взять ниже, чем это следует из теоремы о дискретизации, возникает составляющая с разностной частотой f₀ - f < f_m, которая не подавляется фильтром и присутствует на выходе в виде пульсаций (см. рис. 1.15, в).

При практическом выполнении фильтров возникает проблема, связанная с невозможностью получения импульсов Дирака. Необходимо, как это иллюстрируется рис. 1.14, формировать импульсы с конечными значениями амплитуды и конечной длительностью, т.е. в этом случае не будет выполняться условие предельного перехода (1.17). Подставляя выражение (1.17) в (1.16), получаем для конечного e приближенную импульсную последовательность:

Применяя преобразование Фурье, находим спектр этой последовательности импульсов:

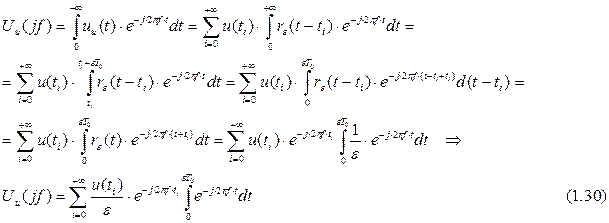
В выражении (1.30) интеграл под знаком суммы представляет собой спектр одиночного импульса с единичной амплитудой и длительностью e×T₀. Экспоненциальный множитель перед интегралом учитывает сдвиг во времени переднего фронта этого импульса на время t_i=i×T₀. Дробь u(t_i) / e представляет собой значение амплитуды i -ого импульса. Воспользовавшись ранее полученным выражением для спектра одиночного импульса длительностью t и амплитудой E (см. соотношение (1.12)), получаем:

Часть последнего выражения, заключенная в фигурные скобки, представляет собой спектр последовательности импульсов Дирака U_d(jf) (см. соотношение (1.28). Таким образом, окончательно имеем:

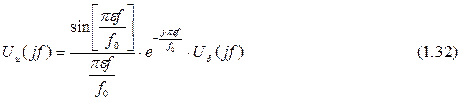
Это тот же спектр, что и для импульсов Дирака, однако с наложением весовой функции вида sinx/x, ослабляющей высокочастотные составляющие. В случае предельного перехода для e ®0 происходит вырождение в последовательность импульсов Дирака с соответствующим преобразованием спектра в U_d(jf) (см. (1.32)). Особенный интерес представляет случай ступенчатой функции (e ®1). Для нее длительность импульса eT₀ равна длительности выборки T₀. Отсюда получаем спектр ступенчатой аппроксимации исходного сигнала (e ®1):

Спектр ступенчатой аппроксимации получается умножением спектра последовательности импульсов Дирака на весовую функцию. На рис. 1.16 представлен спектр амплитуд импульсов Дирака и модуль весовой функции. При максимальной частоте спектра сигнала f_m =0,5 f₀ имеет место ослабление сигнала с коэффициентом 0,64; при максимальной частоте f_m =0,2 f₀, ослабление составляет 0,94. Таким образом, искажения спектра до частоты среза f_m остаются пренебрежимо малыми, если выбрать f₀» 5×f_m.

Для восстановления первоначального сигнала необходим, как показано выше, фильтр нижних частот, который отфильтровывает спектральные составляющие с частотой ниже f_m. Реальный фильтр имеет спад коэффициента усиления конечной крутизны. Чтобы разделить спектральные составляющие, нужно выбрать частоту f₀ также больше 2 f_m. Тогда можно добиться того, что на нижней частоте f₀ - f_m ослабление будет достаточно большим. В этой связи даже целесообразно вместо последовательности импульсов Дирака применить ступенчатую функцию, так как соответствующая весовая функция имеет характер фильтра нижних частот (тем более что ее достаточно просто реализовать на практике с помощью подключенного к выходу ЦАП устройства выборки-хранения).

Искажения спектра в полосе пропускания можно устранить, несколько увеличив коэффициент усиления фильтра нижних частот вблизи частоты среза. Для того чтобы на частотах выше f_m добиться достаточного снижения коэффициента усиления, можно рекомендовать выбрать нулевую точку частотной характеристики вблизи частоты f₀ - f_m.

Таким образом установили, что даже для идеализированных сигналов со строго ограниченным частотным спектром, достаточно точное восстановление сигнала по его дискретным отсчетам возможно лишь при выборе частоты дискретизации в 2-2,5 раза выше, чем это следует из соблюдения граничного условия теоремы отсчетов (т.е. f₀=2×f_max).

Рассмотрим теперь дискретизацию а также восстановление по дискретам реального сигнала, спектр которого, вообще говоря, не является ограниченным. Напомним, что в идеале при соблюдении условия теоремы отсчетов f₀≥2×f_max исходный сигнал восстанавливается по своим дискретам с использованием (1.27), которое в этом случае принимает вид:

Интерполяционный ряд (1.34) носит название ряда Котельникова. Для сигналов со строго ограниченным спектром это выражение является тождеством. Однако спектры реальных сигналов стремятся к нулю лишь асимптотически. Так любой ограниченный во времени непериодический сигнал всегда имеет бесконечный спектр. Поэтому определение верхней границы частотного спектра F_max обычно производится приближенно (например по критерию 90%-ного содержания энергии или средней мощности сигнала).

1) Следовательно, применение равномерной дискретизации к таким сигналам приводит к возникновению в системах обработки информации специфических высокочастотных искажений, обусловленных выборкой (свертка всего первоначального спектра внутрь полосы частот 0… f_дискр /2 – см. «Компьютерра» 11 авг. 1998, с. 23; или см. ниже на этой же странице).

2) Кроме того, и идеальный П-образный фильтр низких частот с граничной частотой F_max, в точности восстанавливающий исходный сигнал в соответствии с (1.34) является физически нереализуемым. Это приводит к проникновению в спектр отфильтрованного дискретизированного сигнала высокочастотных комбинационных составляющих с частотами (f_дискр-F_{сигнала}).

Для уменьшения двух указанных разновидностей высокочастотных искажений необходимо либо увеличивать частоту дискретизации f_дискр=(3…5)f_max, либо использовать перед АЦП дополнительный фильтр низких частот, ограничивающий спектр исходного сигнала перед его аналого-цифровым преобразованием.

Поясним возникновение высокочастотных искажений, обусловленных выборкой (1-ой разновидности) на примере дискретизации звукового сигнала (частотный диапазон 0…20 кГц) на частоте 40 кГц, т.е. при выполнении граничного условия теоремы отсчетов.

Одно из изменений, которое претерпевает спектр сигнала в результате его дискретизации состоит в свертке всего первоначального спектра звукового сигнала, простирающегося примерно от 20 Гц до нескольких сот килогерц, внутрь полосы частот от 0 Гц до половины частоты дискретизации – 20 кГц. Этот процесс изображен на рис. 1.17.

Рис. 1.17. Процесс свертки спектра внутрь частотного диапазона 0…20 кГц

Свертка означает, что все составляющие исходного аналогового сигнала с частотами выше половины частоты дискретизации (а это в основном неслышимые помехи) попадают в слышимый человеческим ухом диапазон частот от 20 Гц до 20 кГц, то есть неслышимые помехи становятся слышимыми, и, таким образом, может резко ухудшиться отношение сигнал/шум.

Все это выглядит весьма непривычно, если не сказать, что вообще противоречит здравому смыслу и упомянутой выше теореме отсчетов! Получается, что происходит дискретизация высокочастотных сигналов с составляющими, лежащими значительно выше не только половины частоты дискретизации, но и самой частоты дискретизации. Однако данное реальное явление иллюстрирует рис. 1.18, на котором показан процесс дискретизации высокочастотного синусоидального сигнала на частоте, которая более чем вдвое ниже частоты самого сигнала.

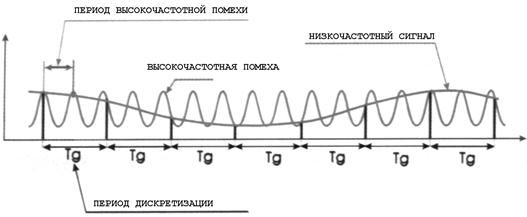
Рис. 1.18. Дискретизация высокочастотной синусоидальной помехи

Хорошо видно, что период колебаний высокочастотной помехи более чем вдвое меньше, нежели период дискретизации. А период, как известно, обратно пропорционален частоте. Значит, частота помехи действительно больше частоты дискретизации. Кроме того, дискретные отсчеты (толстые черные столбики) высокочастотной помехи полностью совпадают с дискретными отсчетами некоторого низкочастотного сигнала (тонкая плавная кривая на рис. 1.18). Таким образом, после дискретизации высокочастотного сигнала мы получили низкочастотный сигнал. Это и есть эффект свертки высокочастотных помех внутрь частотного диапазона от 0 Гц до половины частоты дискретизации.

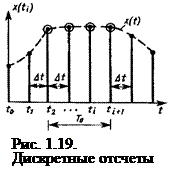Рассмотренная равномерная дискретизации (при Dt = const) иногда может приводить к получению избыточных отсчетов, не оказывающих существенного влияния на процесс восстановления исходного сообщения. Например, если функция x(t) мало изменяется на некотором, достаточно протяженном интервале времени Т₀ (как это показано на рис. 1.19), то соответствующие дискретные отсчеты сигнала практически не отличаются друг от друга и, следовательно, нет необходимости использовать все указанные отсчеты для хранения или передачи информации по линии связи. Сокращение избыточной информации возможно на основе способов адаптивной (неравномерной) дискретизации, обеспечивающих выбор интервала Dt между соседними отсчетами с учетом фактического изменения характеристик сигнала (в частности, скорости его изменения).

1.2.2. Дискретизация по уровню (квантование)

Отличительной особенностью дискретизации по уровню является замена непрерывной шкалы уровней сигнала x(t) дискретной шкалой x_i (i = 1, 2,..., т), в которой различные значения сигнала отличаются между собой не менее чем на некоторое фиксированное (или выбираемое в процессе квантования) значение Dх, называемое шагом квантования. Необходимость квантования вызвана тем, что цифровые вычислительные устройства могут оперировать только с числами, имеющими конечное число разрядов. Таким образом, квантование представляет собой округление передаваемых значений с заданной точностью. При равномерном квантовании (Dх = const) число разрешенных дискретных уровней х, составляет

Где x_max и x_min — соответственно верхняя и нижняя границы диапазона изменения сигнала. Чем меньше значение Dх, тем меньше получаемая ошибка — шум квантования x (х) = х - х_i, которая вычисляется как разность между текущим действительным значением сигнала x(t) и его дискретным представлением х_i. Максимальное значение ошибки квантования зависит от правил округления непрерывной величины x(t) до ее дискретного эквивалента x_i:

1) Усечение — если квантование происходит с отождествлением с нижней границей интервала, то x (х)_max = Dх.

2) Округление — если в результате квантования любое из значений сигнала x(t), попавшее в интервал (х_i – Dх /2; х_i + Dх /2), округляется до х_i, то возникающая при этом ошибка x (х) не превышает половины шага квантования, т. е. max|x(х)| = 0,5Dх.

На практике шаг квантования Dх выбирают, исходя из уровня помех, в той или иной форме присутствующих при измерении, передаче и обработке реальных сигналов.

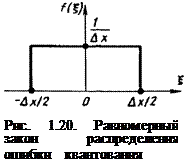
Если функция х(t) заранее неизвестна, а шаг квантования Dх достаточно мал по сравнению с диапазоном изменения сигнала (x_max – x_min), то принято считать ошибку квантования x (х) случайной величиной, подчиняющейся равномерному закону распределения. Тогда при использовании 1-го правила округления плотность вероятности f₁( x) для случайной величины x принимает значение 1/ Dх внутри интервала (0; + Dх) и равна нулю вне этого интервала. При использовании 2-го правила округления, как показано на рис. 1.20, плотность вероятности f₂( x ) для случайной величины x принимает значение 1/ Dх внутри интервала (– Dх /2; + Dх /2) и равна нулю вне этого интервала. Определим среднюю мощность шумов квантования. Для этого необходимо вспомнить некоторые вероятностные характеристики случайных процессов:

Математическое ожидание (mean value) m_x(t) – теоретическая оценка среднего взвешенного значения случайного процесса плотностью вероятности p(x,t) в момент времени t: .

Как несложно догадаться, (а можно и получить из формулы), для 1-го правила округления математическое ожидание ошибки квантования составит половину шага квантования Dx/2, для 2-го — 0.

Дисперсия (variance) характеризует среднюю мощность отклонений случайного процесса от его среднего значения m_x(t) (математического ожидания), называемых флуктуациями (fluctuation):

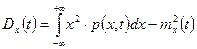
Среднее квадратическое отклонение (standard deviation) – квадратный корень из дисперсии, служит амплитудной мерой разброса значений случайного процесса в момент времени t относительно математического ожидания: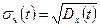

Мощность шумов квантования характеризует дисперсия D( x ) ошибки квантования x. Определим ее для первого и второго правил округления:

1)

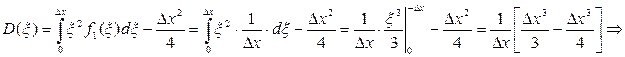
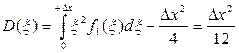(1.36)

2)

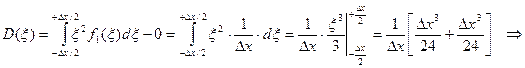
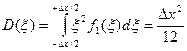(1.36)

Найденная величина прямо пропорциональна мощности шума квантования.

При Dх = const относительная погрешность квантования d(x)=x(х)/х существенно зависит от текущего значения сигнала x(t). В связи с этим при необходимости обработки и передачи сигналов, изменяющихся в широком диапазоне, нередко используется неравномерное (нелинейное) квантование, когда шаг Dх принимается малым для сигналов низкого уровня и увеличивается с ростом соответствующих значений сигнала (например, Dх выбирают пропорционально логарифму значения |х(t)|). Например, при адаптивной разностной компрессии ( ADPCM – Adaptive Differential Pulse Code Modulation), используемой при кодировании междугородних телефонных разговоров, шаг квантования разности величин соседних отсчетов пропорционален средней (или максимальной) амплитуде сигнала на кодируемом временном отрезке.

Относительная погрешность квантования также зависит и от количества уровней квантования, которое при представлении квантуемой величины двоичным кодом равно целой степени числа 2: m=2ⁿ (где m – число уровней квантования). Оценим относительный шум квантования, используя для этого логарифмические единицы децибелы (считая что исследуемый сигнал находится вблизи максимума шкалы и округление происходит по 1-му правилу):

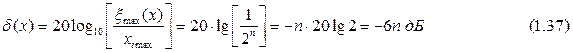
Убедиться на практике в такой зависимости шума квантования от разрядности АЦП можно записывая высококачественный музыкальный сигнал с одинаковой частотой дискретизации (44100 Гц) и разной разрядностью кодового слова например 8 бит и 16 бит. В 1-ом случае будет отчетливо слышна зашумленность (грязный звук), во втором качество будет практически неотличимо от оригинала. (Такой эксперимент можно проделать, используя программу «Фонограф» Windows естественно при наличии в компьютере звуковой 16-битной карты и СDROM).

Отдельный интерес представляет вопрос о соотношении разрядности АЦП, частоты дискретизации сигнала и шума квантования. Допустим сигнал x(t) с частотным спектром, ограниченным частотой f_m, оцифровывается с помощью k -разрядного АЦП на частоте дискретизации f₀=2f_m. Условно серию оцифрованных отсчетов сигнала можно представить как сумму точных дискрет сигнала x(t_i) (без ошибок округления) и ошибок округления Dx(t_i) (шумов квантования), взятых с интервалом 1/(2 f_m) по оси времени. Среднеквадратическое значение шума квантования представляет собой кв. корень из дисперсии (величины пропорциональной мощности шумов квантования (см. соотношение (1.36)) и составляет 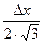(Dx – шаг квантования). Причем этот шум располагается в полосе частот от 0 до половины частоты дискретизации 0…f_m. Таким образом, при оцифровке сигналов размахом (удвоенной амплитудой) А в полный рабочий диапазон АЦП, отношение сигнал/шум в децибелах составит:

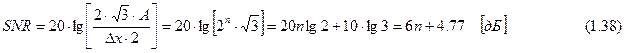
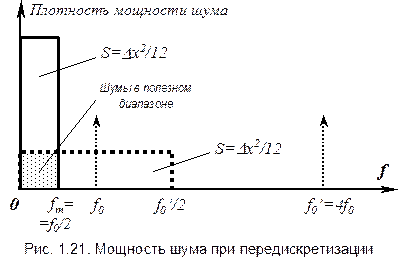Дискретизируем теперь сигнал на частоте в 4 раза превышающей исходную, т.е. на частоте f₀’=8f_m. Представляя оцифрованный сигнал в виде суммы точного ряда дискрет и ряда ошибок округления, заключаем, что дисперсия (мощность шума) не изменилась оставшись равной прежней величине 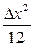. Но теперь в результате увеличения частоты дискретизации этот шум располагается в полосе частот от нуля до половины новой частоты дискретизации 0…4 f_m. (см. рис. 1.21). А наш полезный сигнал в оцифрованном виде как и раньше будет иметь спектр, простирающийся до частоты f_m. Таким образом, спектр шума стал в четыре раза шире спектра полезного сигнала при прежней мощности шума. Отсюда следует, что мощность шума внутри спектра полезного сигнала 0…f_m упадет в 4 раза (или среднеквадратичное значение шума уменьшится в 2 раза), а это равносильно увеличению отношения сигнал/шум на 6 дб:

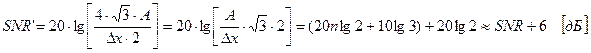
Описанный процесс можно продолжать. При этом каждое увеличение частоты дискретизации в 4 раза создает условия для улучшения отношения сигнал-шум на 6 дб, что равносильно увеличению разрядности АЦП на один двоичный разряд (см. соотношения 1.37, 1.38). Исходя из вышесказанного, уровень шумов принято оценивать по формуле:

,

где n – разрядность АЦП (количество двоичных разрядов), f_m – максимальная частота спектра дискретизируемого сигнала, C_S – постоянная, учитывающая форму сигнала (для гармонических сигналов C_S =1,7 дБ, для обычных звуковых сигналов C_S = –15…+2 дБ). Наличие слагаемого C_S обусловлено зависимостью шума квантования от параметров дискретизируемого сигнала (корреляцией шума с сигналом).

Следует отметить, что указанное увеличения отношения сигнал-шум можно реализовать при условии цифровой фильтрации дискретизированного сигнала перед окончательным восстановлением его непрерывной формы на выходе. С помощью цифрового фильтра с большим ослаблением шума в полосе задержания и узкой переходной полосой (а сделать такой цифровой фильтр не составляет большого труда в отличие от аналогового) можно подавить полосу от f_m до 4ⁿ×f_m кГц, содержащую только шумы квантования, и получить лучшее на 6n дБ отношение сигнал/шум квантования.

Таким образом, квантователь АЦП не обязательно должен иметь высокую разрядность, чтобы выходной поток цифровых данных АЦП тоже имел таковую. Увеличить эффективную разрядность АЦП можно, используя метод оверсэмплинга (передискретизации ) и цифровой фильтрации (см. главу 4).

1.3. Коды и кодирование

1.3.1. Количественное измерение информации в сигнале

Рассмотрим вопрос о количественном измерении информации, доставляемой сигналом. Как уже говорилось, реальный сигнал можно заменить его упрощенной дискретной моделью, согласно которой существенными (информативными) считаются лишь те его значения, которые соответствуют ближайшим узлам решетки (сетки), полученной в результате дискретизации сигнала по времени и уровню (рис. 1.22). Если сигнал имеет конечную длительность Т, то число его дискретных отсчетов во времени можно приближенно оценить с помощью теоремы Котельникова: n=T/Dt=2F_maxT. Здесь F_max — максимальная частота в спектре сигнала х(t). Число уровней сигнала x(t) определяют соотношением (1.35), где шаг квантования Dх определяется требуемой точностью обработки информации.

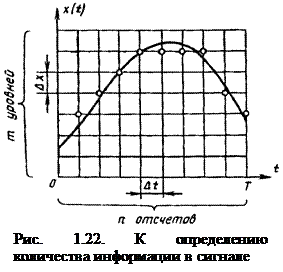Полагая, что количество информации, которое можно перенести сигналом, будет тем больше, чем больше число возможных сообщений (комбинаций сигнала), дадим оценку числу таких сообщений в рассматриваемом случае. Так как в каждый дискретный момент времени сигнал может принимать одно из т значений, то с помощью двух соседних отсчетов сигнала можно передать уже m² различных сообщений, за три отсчета – т³ сообщений и т. д. В общем случае число различных комбинаций сигнала за время T=nDt составляет N = тⁿ.

Полученное таким образом число N дает комбинаторную оценку информации, содержащейся в произвольном дискретном сообщении (слове) из n элементов (букв), каждая из которых принимает одно из т возможных значений, составляющих вместе некоторый алфавит. (Так, с помощью двухразрядного десятичного числа можно записать 100 различных чисел от 0 до 99. При средней длине слова в русском языке n = 5 и алфавите с т = 32 буквами можно составить 33,5 миллиона различных слов 32⁵=(2⁵)⁵=2²⁵»32 000 000.)

Вместе с тем использование N в качестве меры информации неудобно, так как в данном случае не выполняется условие аддитивности, т. е. пропорциональности между длиной слова (длительностью сигнала) и количеством содержащейся в нем информации. Между тем удвоение времени передачи должно приводить к удвоению количества передаваемой информации.

Р. Хартли предложил в качестве меры количества информации использовать логарифм числа возможных сообщений:

Согласно (1.40), количество информации в сигнале пропорционально длительности сигнала (числу отсчетов n). Выбор основания логарифма а влияет лишь на размерность, т. е. на единицу измерения количества информации. Наиболее часто принимается а = 2, при этом значение I измеряется в битах. 1 бит — это количество информации, соответствующее одному из двух равновозможных состояний (да - нет, включить - выключить, исправно — неисправно). В вычислительной технике 1 бит обозначает 1 двоичный разряд - символ, принимающий значение 0 или 1. В качестве единицы представления данных в ЭВМ используется байт — слово (набор) из восьми двоичных разрядов (битов). Легко видеть, что байтом можно передать одно из 2⁸ = 256 различных сообщений.

1.3.2. Выбор вида модуляции для передачи сообщения

1) Рассмотрим амплитудно-импульсную модуляцию, широко распространенную при построении аналого-цифровых преобразователей (АЦП). Носителем информации при АИМ является периодический импульсный сигнал u_н(t), вид которого определяется тремя заданными параметрами: амплитудой Е (далее принимаем Е = 1), длительностью t и периодом следования Т (или частотой основной гармоники w₀ = 2p/T).

Полагаем, что сигнал u(t) на выходе модулятора описывается уравнением

u(t)=[U₀+x(t)]u_н(t) (1.41)

где U₀ — амплитуда импульсов при равенстве нулю входного сигнала x(t)=0. На рис. 1.23 показана временная диаграмма модулированного сигнала u(t) для случая x(t)=U_mcos(Wt+j), где W<w₀. Определим частотный спектр амплитудно-модулированного импульсного сигнала с гармонической огибающей.

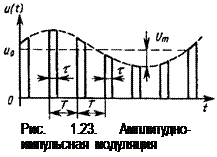Следовательно, сигнал u(t) является периодическим и его спектр амплитуд (рис. 1.24) содержит кроме постоянной составляющей и гармоники с частотой W также высокочастотные гармоники с частотами кратными основной (тактовой) частоте импульсного сигнала w₀, и, кроме того, гармоники с боковыми частотами kw₀±W. В общем случае, когда спектр модулирующего сигнала x(t) занимает некоторую полосу частот (0... W_max), по обе стороны от каждой из спектральных линий с частотами kw₀ располагаются боковые полосы частот шириной 2W_max. (Приблизительно то же самое было показано при доказательстве теоремы отсчетов, когда информационный сигнал модулировал по вольт-секундной площади периодическую последовательность d-импульсов).

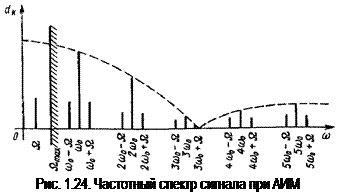Общая ширина частотного спектра АИМ-сигнала определяется необходимостью пропускания периодической последовательности импульсов, а не исходным модулирующим сигналом. Из графика также следует, что сигнал х(t) можно восстановить с помощью фильтра низких частот, имеющего полосу пропускания от 0 до W_max. Для неискаженного выделения сигнала необходимо, чтобы другие составляющие спектра не попали в данную полосу частот. Ближайшей к полосе пропускания фильтра является составляющая (w₀ – W_max). Поэтому условие отсутствия искажений принимает вид W_max < (w₀ – W_max ) или w₀ >2W_max что полностью согласуется с теоремой Котельникова.

Помехоустойчивость АИМ весьма мала, так как помехи, действующие на сигнал в процессе его передачи, искажают прежде всего амплитуду импульса, поэтому АИМ обычно применяют в комбинациях с другими видами модуляции.

Одним из наиболее перспективных видов модуляции считается кодоимпульсная модуляция (КИМ), при которой каждый отсчет сигнала x(t) передается кодовой комбинацией, состоящей из нескольких импульсов.

1.3.3. Основные характеристики кодов, выбор оптимальной значности кода

Процесс преобразования сообщения в дискретный сигнал называют кодированием информации, а множество различных кодовых комбинаций, получаемых при данном правиле кодирования – кодом.

Важной характеристикой кода является основание (или значность) кода m, т. е. число возможных значений, которые могут принимать элементы (символы, буквы) кодовой комбинации.

Пусть требуется передать сигнал, уровень которого изменяется от 0 до 10 В. Если погрешность представления данных составляет 10 мВ, то каждый отсчет сигнала можно рассматривать как одно из 1000 возможных сообщений. Для передачи этой информации можно предложить различные способы:

а) каждому сообщению поставить в соответствие определенный уровень напряжения, при этом основание кода т = 1000, а длина кодовой комбинации (слова) принимает минимальное значение n =1;

б) можно воспользоваться двоичным (бинарным) сигналом с т= 2, но тогда потребуется комбинация длины n = 10 (2¹⁰ = 1024), так что некоторые комбинации здесь не использованы. Возможны и промежуточные варианты. Поэтому целесообразно поставить вопрос об определении оптимальной пары значений т (значности кода) и n (длины кодового слова).

В качестве критерия оптимальности примем минимум произведения числа требуемых символов (уровней) m на длину кодовой комбинации n, необходимой для представления заданного числа сообщений N. В общем случае, если значность кода m, то для передачи N сообщений, потребуется комбинация длиной n, причем должно выполняться неравенство mⁿ³N. Отсюда

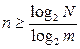
Тогда можно записать

А указанное условие минимума принимает вид

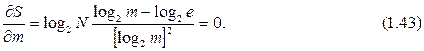
или т = е. Как видно для задачи о передаче N сообщений, наиболее экономное представление множества сообщений соответствует m = 2, 3.

Таким образом, код с основанием m = 2 (двоичный) оказывается не только удобным вследствие легкости формирования бинарных сигналов (низкий и высокий уровень напряжения), но и одним из наиболее экономных.

Примером двоичного кода является запись натурального числа А в позиционной двоичной системе счисления, осуществляемая по следующему правилу:

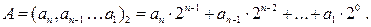
Здесь символы a₁, a₂,…a_n принимают значения 0 или 1, n - число разрядов в коде. Предполагается, что символ a_n, расположенный в старшем разряде кодовой комбинации, имеет наибольший вес 2^n-1, тогда как вес символа a₁ в младшем разряде является минимальным и равен 2⁰=1.

Для представления дробных чисел, значения которых не превышают единицы, обычно используют запись в следующем виде:

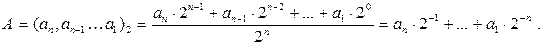
Рассмотренный код относится к арифметическим кодам, на которые распространяются арифметические операции сложения, вычитания, умножения, деления.

Примером кода, отличного от арифметического, является код Грея, обладающий тем ценным свойством, что любые 2 соседние кодовые комбинации отличаются лишь значением одного разряда. Он используется при построении различных преобразователей аналог-код, что позволяет свести к ЕМР ошибку неоднозначности при считывании информации.

1.3.4. Помехозащищенное кодирование

В процессе передачи и хранения информации, представленной в двоичном коде, могут возникать ошибки, связанные с изменением отдельных дискретных символов (0 вместо 1 и 1 вместо 0), вследствие действия помех.Этиошибки носят случайный характер и нередко приводят к существенным искажениям передаваемой информации (примером являются ошибки в старших разрядах кодовой комбинации при передаче числовой информации). Обеспечить помехоустойчивость можно, применяя корректирующие или помехозащищенные коды, позволяющие своевременно обнаруживать и исправлять возникающие ошибки.

К. Шеннон доказал, что если скорость передачи информации через канал с помехами не превышает его пропускной способности, то всегда можно построить такой код, при котором вероятность безошибочного декодирования будет сколь угодно близка к единице. Под пропускной способностью канала понимается максимально возможная для данного канала скорость передачи информации C [бит/c], которую находят по соотношению Хартли–Шеннона

где F_k - полоса частот канала в Гц; Р_с и P_пом — средние мощности полезного сигнала и помехи.

(Сравните пропускная способность канала в отсутствие шума, установленная законом Хартли, определяется в виде: 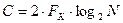, где N – число уровней кодирования (2 в двоичной системе)).

Идея построения корректирующих двоичных кодов предложена Р. В. Хеммингом. Для ее пояснения введем понятие кодового расстояния между двумя числами, закодированными в двоичном коде. Кодовое расстояние двух чисел A₁ и A₂ есть количество единиц в их сумме по модулю 2 (операция поразрядного исключающего ИЛИ). Попросту говоря, это количество отличающихся двоичных разрядов в указанных кодовых комбинациях.

Пусть восемь кодовых комбинаций для 3-разрядного двоичного кода являются разрешенными (допустимыми), тогда кодовое расстояние между соседними комбинациями d = 1. Например соседней кодовой комбинацией нуля (000) является восемь (100).Так как в данном случае отсутствует какой-либо признак, позволяющий судить о появлении ошибки в кодовой комбинации, то такой код не является помехозащищенным.

Допустим, что лишь четыре из восьми кодовых комбинаций считаются разрешенными, например это комбинации 001, 010, 100 и 111. Тогда кодовое расстояние d = 2, причем искажение символа в одном из разрядов приводит к получению запрещенной кодовой комбинации (000, 011, 101 или 110), что легко выявляется при проверке. Полученный таким образом двоичный код называют кодом с обнаружением одиночной ошибки. Здесь присутствует выигрыш, состоящий в том что одиночная ошибка обнаруживается, и проигрыш в том что при той же разрядности слова уменьшилось число информационных разрядов (n=2). Т.е. теперь можно закодировать лишь числа от 0 (00) до 3 (11).

Для d = 3 в качестве разрешенных кодовых комбинаций можно принять, например, 010 и 101. При этом обеспечивается возможность не только обнаружения, но и исправления одиночной ошибки. Действительно, получение запрещенной кодовой комбинации 110 указывает на наличие ошибки, для исправления которой необходимо перейти к ближайшей из разрешенных кодовых комбинаций (в данном случае — 010). Данный код позволяет обнаруживать и двойные ошибки, так как при одновременном искажении символов в двух разрядах кодовой комбинации последняя также попадает в число запрещенных за счет еще большего проигрыша в длине слова несущего полезную информацию (1 разряд).

Из сказанного следует, что построение помехозащищенных кодов всегда связано с введением избыточности в передаваемые кодовые комбинации. При этом корректирующая способность кода, т. е. число обнаруживаемых и исправляемых с его помощью ошибок, определяется главным образом кодовым расстоянием. В общем случае минимальное кодовое расстояние

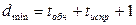
Где t_обн – число обнаруживаемых ошибок; t_испр – число исправляемых ошибок. Если код позволяет только обнаруживать ошибки, не исправляя их, то d_min=t_обн+1. Для кода, исправляющего все обнаруженные ошибки, d_min=2t_испр+1.

Наиболее вероятными являются ошибки единичной кратности. Их и следует обнаруживать и исправлять в первую очередь.

Простейшим из помехозащищенных кодов является код с проверкой на четность (d = 2), который используется при вводе и хранении информации в ЭВМ (часто при записи и извлечении из ОЗУ). В данном случае к кодовой комбинации, состоящей из n информационных разрядов а_n, а_n-1,.... а₁, добавляется один дополнительный (проверочный) разряд a₀ так, что кодовая комбинация принимает вид

Значение проверочного разряда а₀ вычисляют сложением по модулю 2 значений всех информационных разрядов:

Иначе говоря, а₀ = 0, если общее количество единиц в информационных разрядах кодовой комбинации является четным числом, или а₀ = 1, если это число нечетно. Но тогда при отсутствии ошибки кодовая комбинация всегда содержит четное число единиц и, следовательно, сумма

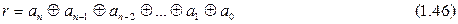
должна принимать нулевое значение (r = 0). Если в результате проверки установлено, что контрольная сумма (1.46) принимает значение r = 1, то это указывает на наличие одиночной ошибки в принятой кодовой комбинации. Недостатком данного кода является отсутствие возможности автоматической коррекции ошибок.

Примером корректирующего кода, позволяющего обнаружить и исправить одиночную ошибку (d = 3), является код Хемминга, идея построения которого заключается в следующем. Допустим, что кодовая комбинация содержит n информационных и k проверочных разрядов, причем значение каждого проверочного разряда определяется суммированием по модулю 2 определенного числа информационных разрядов. После приема кодовой комбинации производят k проверок, заключающихся в вычислении контрольных сумм r₁, r₂, … r_k для определенных наборов значений из всех (n + k) разрядов. Если записать результаты данных проверок справа налево, то получим k -разрядное контрольное число r = (r_k, r_k-1, … r₁), которое и указывает номер искаженного разряда в двоичной системе счисления. Отсутствию ошибки в кодовой комбинации соответствует контрольное число r, составленное только из нулей.

Таблица 1.1. Результаты расчета количества контрольных разрядов в коде Хемминга

n	k	n+k	R=k/(n+k)
			0,67
			0,6
			0,5
			0,43
			0,44
			0,4
			0,36
			0,33
			0,24

Это число должно описывать (n + k + 1) различных событий, включая отсутствие ошибки или искажение одного из (n + k) разрядов. Так как в k двоичных разрядах можно записать лишь 2^k различных контрольных чисел, то обязательным является выполнение условия

откуда можно найти требуемое значение k для заданного числа n. (см. табл. 1)

Результаты проверок r₁, r₂, … r_k в коде Хемминга вычисляются в соответствии с проверочными уравнениями (1.48).

Первое уравнение включает в себя те разряды кодовой комбинации, в номерах которых в двоичной форме записи стоит единица в младшем разряде (при 2⁰). Второе представляет собой сумму по модулю 2 всех разрядов, в двоичных номерах которых стоит единица на позиции 2¹, т. е. в предпоследнем разряде. Третье составлено как сумма по модулю 2 тех разрядов, в двоичных номерах которых имеется единица на третьем месте, считая с конца (т. е. при 2²), и т. д.

Анализ уравнений (1.48) показывает, что разряды a₁, a₂, a₄…входят только по одному разу в каждое из этих уравнений. Поэтому именно эти разряды удобно принять в качестве проверочных. Приравнивая проверочные уравнения к нулю при отсутствии ошибок, т. е. Полагая r₁=r₂=…=r_k=0, можно найти требуемые значения проверочных разрядов:

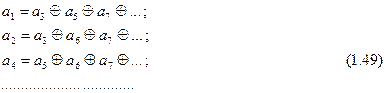
Так как информационные и проверочные разряды в полученной кодовой комбинации строго разграничены (разнесены), код Хемминга относят к разделимым кодам (в неразделимых кодах обычно отсутствует четкое деление на информационные и проверочные разряды).

На практике также широко распространена группа корректирующих кодов, называемых циклическими. Эти коды хорошо приспособлены для обнаружения и исправления не только одиночных ошибок, но и ошибок высокой кратности (пакетов ошибок), имеют простые кодирующие и декодирующие устройства.

При построении циклического кода удобно представить кодовую комбинацию в виде полинома:

,

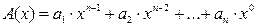где х — фиктивная переменная, заменяющая собой число 2 — основание системы счисления. Так, например, от комбинации А = (1011)₂ = 1×2³+0×2² + 1×2¹ + 1×2⁰ можно перейти к полиному А (х) = 1× х³ + 0 × х² + 1× х¹ + 1×х⁰ = х³ + х + 1. Над полиномами можно производить любые алгебраические операции, как и над двоичными числами. Исключение составляет сложение, которое должно производиться только по модулю 2: 0 × хⁱ + 0 × хⁱ = 0×х ⁱ; 0 × хⁱ + 1 × хⁱ = 1×х ⁱ; 1× хⁱ + 0 × хⁱ = 1×х ⁱ; 1× хⁱ + 1 × хⁱ = 0×х ⁱ. Как следствие, –1× хⁱ = 1× хⁱ, т. е. вычитание заменяется сложением.

Циклические коды образуются путем умножения комбинации исходного кода, выраженной в виде полинома А(х) степени (n – 1), на образующий полином G(x) степени k (в соответствии с указанным правилом, разрешенными считаются лишь те кодовые комбинации, которые делятся без остатка на полином G(x)). В качестве образующего полинома G(x) обычно выбирают какой-либо неприводимый полином от аргумента х, т. е. такой, который не может быть представлен в виде произведения сомножителей — полиномов с вещественными коэффициентами. К неприводимым полиномам относятся: G(х) = х + 1; G (х) = х² + х + 1; G (х) = х³ + х² + 1; G (х) = х³ + х + 1; G (х) = х⁴ + х³ + 1 и т. д. Степень k образующего полинома G(x) задается исходя из требования к корректирующей способности кода. Так, если циклический код должен обеспечивать обнаружение и исправление одиночной ошибки, то для определения значения k можно воспользоваться условием (1.47).

Характерное свойство циклических кодов — при циклической перестановке символов кодовой комбинации получается другая комбинация этого же кода. Например, если A₁ = (1011)₂ - комбинация циклического кода, то A₂ = (0111)₂ — также комбинация этого кода.

Пример. Для кодовой комбинации А = (1001); имеем A(x)=x³+1. Так как п = 4, то для кода с обнаружением и исправлением одиночной ошибки, с учетом (1.47), принимаем k = 3. Выбираем G (х) = х³ + х² + 1. Перемножая полиномы А (х) и G (х), получаем F (х) = А (х) G (х) = х⁶ + х⁵ + х² + 1, т. е. комбинация циклического кода принимает вид F = (1100101)₂.

Декодирование циклического кода сводится к делению кодовых комбинаций на образующий полином G(x). Если полученный при этом остаток R (х) отличен от нуля, то это указывает на наличие ошибки, которая должна выявляться с помощью специальной логической схемы.

1.4. Структура цифровой системы записи-воспроизведения звука на основе оптического компакт-диска

В заключение этого раздела приведем структурную схему реального ЭПУ – системы цифровой передачи звука (например цифровая система записи-воспроизведения на/с оптический компакт диск) [10].

Принцип, на котором базируется способ передачи звуковых сигналов в цифровой форме, состоит в том, что полное воспроизведение любого сигнала на стороне приема возможно и в том случае, когда передается не весь сигнал, а лишь периодически выделяемые из него отсчеты. Очевидное техническое достоинство такого способа передачи ничтожное влияние внешних помех на полученные в результате преобразования импульсные сигналы. Обработка цифровых сигналов проводится устройствами, легко поддающимися интеграции и обладающими высокой временной стабильностью свойств.

Обобщенная структурная схема системы цифровой звукопередачи показана на рис. 1.25. Аналоговый (непрерывный во времени) сигнал источника подается на фильтр, ограничивающий его частотную полосу. Затем из аналогового сигнала с помощью схемы выборки хранения выделяются отсчеты, т.е. производится квантование сигнала во времени. Далее сигнал поступает на АЦП, который преобразует амплитуду каждого отсчета в закодированные числа. Они и представляют собой цифровые сигналы, дискретные во времени и по величине. Для защиты от возможных ошибок, а также для согласования с параметрами канала передачи цифровой сигнал, как правило, перекодируется путем введения контрольных символов (избыточность). На приемной стороне с помощью ЦАП вырабатывается сигнал, амплитуда которого в каждый момент времени соответствует амплитуде отсчета на стороне передачи. Наконец, сигнал подается на фильтр НЧ, который позволяет восстановить непрерывный во времени (аналоговый) сигнал.

2. Цифроаналоговые преобразователи (ЦАП)

При построении устройств, связывающих ЭВМ с объектами, использующими информацию в непрерывной форме, требуется преобразование информации из цифровой формы в аналоговую (непрерывную) и из аналоговой в цифровую (см. рис. 2.1.). Цифроаналоговые преобразователи (ЦАП) широко используется там, где необходимо с помощью цифровой информации, выдаваемой ЭВМ, управлять аналоговыми устройствами, например, осуществлять перемещения клапана, пропорциональные рассчитанному значению цифрового сигнала. Кроме того, ЦАП используются в составе аналого-цифровых преобразователей (АЦП) для формирования опорного аналогового сигнала (тока или напряжения), с которым сравнивается преобразуемый сигнал (см. ниже АЦП).

Рассмотрим сначала цифро-аналоговое преобразование, поскольку оно проще с точки зрения принципа действия и способа построения, и, кроме того, ЦАП иногда на практике используются как компоненты аналого-цифровых преобразователей (АЦП).

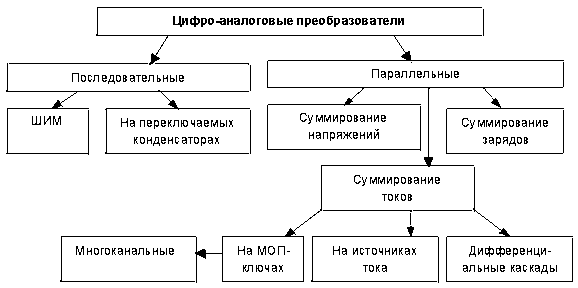
Рис. 2.2. Классификация ЦАП

Цифроаналоговым преобразователем (ЦАП) называется устройство, осуществляющее автоматическое преобразование входных значений, представленных числовыми кодами в эквивалентные им значения какой-нибудь физической величины (напряжения, тока). Преобразование обеспечивает соответствие между входным числовым значением N, и ее аналоговым эквивалентом x(t). Количественная связь для любого момента времени t, определяется соотношением х(t)=N_ti×Dx±dx_i, где Dx — шаг квантования по уровню (аналоговый эквивалент единицы младшего разряда кода); dx_i - погрешность преобразования.

Цифро-аналоговый преобразователь (ЦАП) предназначен для преобразования числа, определенного, как правило, в виде двоичного кода, в напряжение или ток, пропорциональные значению цифрового кода. Схемотехника цифро-аналоговых преобразователей весьма разнообразна. На рис. 2.2 представлена классификационная схема ЦАП по схемотехническим признакам. Кроме этого, ИМС цифро-аналоговых преобразователей классифицируются по следующим признакам:

· По виду выходного сигнала: с токовым выходом и выходом в виде напряжения

· По типу цифрового интерфейса: с последовательным вводом и с параллельным вводом входного кода

· По числу ЦАП на кристалле: одноканальные и многоканальные

· По быстродействию: умеренного и высокого быстродействия

2.1. Параллельные ЦАП

2.1.1. ЦАП с cуммированием весовых токов (с двоично-взвешенными сопротивлениями)

ЦАП с весовыми двоично-взвешенными сопротивлениями (рис. 2.3) состоит из следующих компонентов:

1) n ключей, по одному на каждый разряд, управляемых преобразуемым двоичным кодом N;

2) матрицы двоично-взвешенных резисторов; источника опорного напряжения U_оп;

3) выходного операционного усилителя, с помощью которого суммируются токи, протекающие через двоично-взвешенные сопротивления, для получения аналогового выходного сигнала U_вых пропорционального цифровому коду.

Регистр, который обычно является внешним устройством по отношению к ЦАП, вырабатывает двоичный код N, состоящий из n двоичных разрядов:

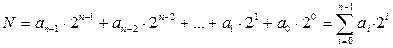
Каждый i-й разряд управляет ключом S_i который подключается к инвертирующему входу ОУ, когда a_i = 1, или к общей шине, когда a_i = 0. Сопротивления резисторов, соединенных с ключами, таковы, что обеспечивается пропорциональность протекающего в них тока двоичному весу соответствующего разряда входного кода. Сопротивление резистора в младшем разряде имеет значение R, сопротивление следующего резистора R/2 и т. д. до сопротивления резистора в старшем разряде, значение которого R/2^n-1. ОУ включен по схеме инвертирующего суммирующего усилителя, следовательно выходное напряжение определяется как

Максимальное выходное напряжение имеет место, когда все разряды примут значение равное 1.

Номиналы сопротивлений в младшем и старшем разрядах отличаются в 2^n-1 раз и должны быть выдержаны с высокой точностью. Например, для 12-разрядного ЦАП использование в старшем разряде сопротивления 10кОмпотребует включения в младший разряд преобразователя сопротивления порядка 20 МОм. Это создает трудности при реализации ЦАП посредством интегральной технологии. К тому же к точности резисторов старших разрядов предъявляются более жесткие требования, поскольку разброс токов в них не должен превышать половины единицы младшего разряда. Поэтому разброс сопротивления в k-м разряде должен быть меньше, чем

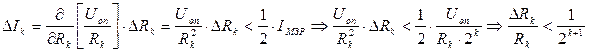(2.2)

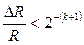(2.3)

Из этого условия следует, что разброс сопротивления резистора, например, в четвертом разряде (2⁴)не должен превышать 3%, а в 10-м разряде (2¹⁰) – 0,05% и т.д.

Рассмотренная схема при всей ее простоте обладает следующими недостатками:

1) значения сопротивлений весовых резисторов могут различаться в тысячи раз, а это делает весьма затруднительной реализацию этих резисторов в полупроводниковых ИМС.

2) сопротивление резисторов старших разрядов в многоразрядных ЦАП может быть соизмеримым с сопротивлением замкнутого ключа, а это приведет к погрешности преобразования.

2.1.2. ЦАП на основе матрицы R–2R

Эти недостатки устранены в схеме ЦАП AD7520 (отечественный аналог 572ПА1), разработанном фирмой Analog Devices в 1973 году, которая в настоящее время является по существу промышленным стандартом (по ней выполнены многие серийные модели ЦАП). Указанная схема представлена на рис. 2.4. В качестве ключей здесь используются МОП-транзисторы.

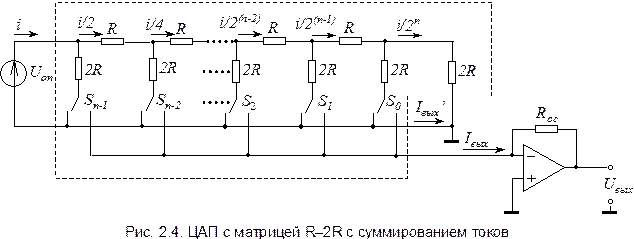
В этой схеме задание весовых коэффициентов ступеней преобразователя осуществляют посредством последовательного деления опорного напряжения с помощью резистивной матрицы постоянного импеданса. Основной элемент такой матрицы представляет собой делитель напряжения (рис. 2.5), который должен удовлетворять следующему условию: если он нагружен на сопротивление R _н, то его входное сопротивление R _вх также должно принимать значение R _н. Коэффициент ослабления цепи a= U ₂/ U ₁ при этой нагрузке должен иметь заданное значение. При выполнении этих условий получаем следующие выражения для сопротивлений:

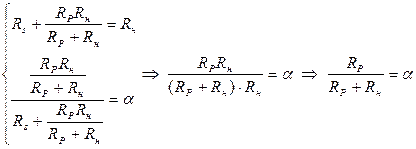
(2.4)

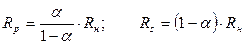(2.5)

При двоичном кодировании a =0,5. Если положить R_н =2 R, то

R_s=R и R_p=2R (2.6)

в соответствии с рис. 2.5.

Поскольку в любом положении переключателей S_k они соединяют нижние выводы резисторов с общей шиной схемы, источник опорного напряжения нагружен на постоянное входное сопротивление R _вх= R. Это гарантирует неизменность опорного напряжения при любом входном коде ЦАП.

Согласно рис. 2.4, выходные токи схемы определяются соотношениями:

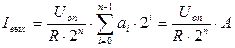(2.7)

(2.8)

выходное напряжение:

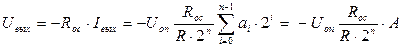(2.9)

а входной ток:

(2.10)

Поскольку нижние выводы резисторов 2 R матрицы при любом состоянии переключателей S_i соединены с общей шиной схемы через низкое сопротивление замкнутых ключей, напряжения на ключах всегда небольшие, в пределах нескольких милливольт. Это упрощает построение ключей и схем управления ими и позволяет использовать опорное напряжение из широкого диапазона, в том числе и различной полярности. Поскольку выходной ток ЦАП зависит от U _оп линейно (см. (2.7)), преобразователи такого типа можно использовать для умножения аналогового сигнала (подавая его на вход опорного напряжения) на цифровой код. Такие ЦАП называют перемножающими (MDAC).

В рассмотренной схеме ЦАП используется токовый режим работы суммирующего элемента, т.е. ОУ выполняет суммирование токов. Несложно видеть, что выходной ток I_вых определяется как

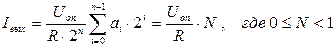(2.11)

Формирование разрядных токов в рассматриваемых ЦАП осуществляется с помощью ключей, коммутирующих токи (токовых ключей). Потенциалы между контактами таких ключей близки к 0, и следовательно переходные процессы протекают быстрее. По таким схемам (с КМОП токовыми ключами) реализованы ИМС 10- и 12-разрядных ЦАП К572ПА1, К572ПА2 (рис. 2.6) с временем преобразования соответственно 5 мкс и 15 мкс. Отличие К572ПА2 от К572ПА1 состоит в наличие двух последовательно включенных регистров RG1 и RG2, позволяющих записывать и хранить цифровую информацию, а также управлять аналоговыми переключателями тока (RG2). Это делает данную БИС удобной для организации связи с микропроцессором.

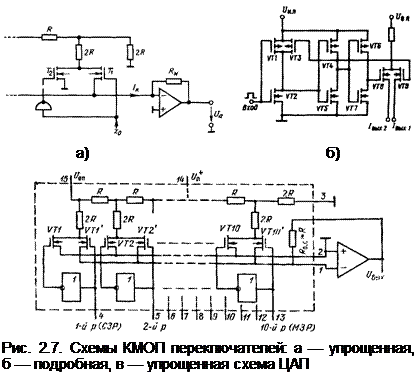Упрощенная схема КМОП переключателя представлена на рис. 2.7, а, на рис. 2.7, б представлена более подробная схема. В этойсхеметранзисторы VT1, VT2 служат для согласования с микросхемами на входе ЦАП, транзисторы VT4—VT7 используются для управления ключевыми транзисторами VT8, VT9, которые подключают разрядные токи резистивной матрицы к одной из двух выходных шин. Через транзистор VT3 осуществляется положительная обратная связь для уменьшения времени переключения.

Точность ЦАП на КМОП-ключах снижает то обстоятельство, что при высокой разрядности необходимо согласовывать сопротивления R ₀ ключей с разрядными токами. Особенно это важно для ключей старших разрядов. Например, в 10-разрядном ЦАП AD7520 (MAX7521 – 1474.pdf) ключевые МОП-транзисторы шести старших разрядов сделаны разными по площади и их сопротивление R ₀ нарастает согласно двоичному коду (20, 40, 80, …, 640 Ом). Таким способом уравниваются (до 10 мВ) падения напряжения на ключах первых шести разрядов, что обеспечивает монотонность и линейность переходной характеристики ЦАП. 12-разрядный ЦАП 572ПА2 имеет дифференциальную нелинейность до 0,025% (1 МЗР).

ЦАП на МОП ключах имеют относительно низкое быстродействие из-за большой входной емкости МОП-ключей. Тот же 572ПА2 имеет время установления выходного тока при смене входного кода от 000...0 до 111...1, равное 15 мкс. 12-разрядный DAC7611 фирмы Burr-Braun имеет время установления выходного напряжения 10 мкс. В то же время ЦАП на МОП-ключах имеют минимальную мощность потребления. Тот же DAC7611 потребляет всего 2,5 мВт. В последнее время появились модели ЦАП рассмотренного выше типа с более высоким быстродействием. Так 12-разрядный AD7943 (1389.pdf) имеет время установления тока 0,6 мкс и потребляемую мощность всего 25 мкВт. Малое собственное потребление позволяет запитывать такие микромощные ЦАП прямо от источника опорного напряжения. При этом они могут даже не иметь вывода для подключения ИОН, например, AD5321.

Примерами ЦАП рассматриваемого типа являются также MAX5480 (1784.pdf), AD7524 (1297.pdf), AD7533 (1299.pdf), AD7542 (1306.pdf).

Основные схемы включения

1) Как видно из (2.9), выходное напряжение ЦАП при включении внешнего ОУ (рис. 2.4) пропорционально произведению дробного значения входного кода N и опорного напряжения U_оп:

Таким образом ЦАП можно использовать в качестве умножителя двух сигналов: цифрового и аналогового. Малая зависимость сопротивления открытого ключа на МОП-транзисторе от амплитуды и направления протекающего тока (линейный участок выходной характеристики) в КМОП-ЦАП позволяет изменять U_оп по амплитуде и знаку в пределах -17…17В. Если вторую функцию подать в цифровом виде на входы разрядов a₉…a₀, то на выходе ЦАП будет сигнал пропорциональный произведению аналогового и цифрового сигналов (перемножающий ЦАП). Таким образом с помощью основной схемы включения (рис. 2.4) можно реализовать двухквадрантное умножение. При этом используется двуполярный источник сигнала, подключаемый ко входу опорного напряжения U_оп и обычный n-разрядный двоичный код. Реальная схема двухквадрантного перемножителя на основе MAX5480 и внешнего ОУ приведена на рис. 2.8, б.

а) б)

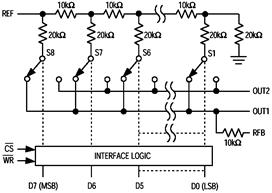
Рис. 2.8. Структурная схема ЦАП MAX5480 (a) и схема двухквадрантного перемножителя на ее основе (б)

Рассмотренное свойство умножающего ЦАП используется также для усиления аналогового сигнала с переменным коэффициентом, когда коэффициент усиления аналогового сигнала модулируется входным цифровым кодом (усилитель с программируемым коэффициентом передачи). При этом усиливаемый аналоговый сигнал подается на вход U_оп (V_ref).

2) Умножающий ЦАП также может быть использован и для делениявходного аналогового напряжения на число. Для этого его охватывают цепью отрицательной обратной связи (рис. 2.9).

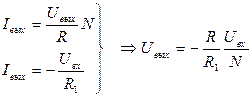
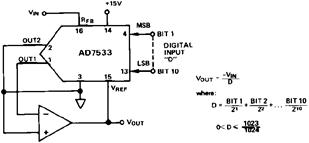
Рис. 2.9. Устройство деления аналоговой величины на код

3) До сих пор при описании ЦАП цифровая входная информация представлялась в виде чисел, не имеющих знака. Обработка чисел со знаком имеет определенные особенности. Обычно двоичные числа с любым знаком представляются с использованием дополнительного двоичного разряда. Например, с помощью 8 разрядов можно представить числа в диапазоне -128…+127 (дополнительный код). При вводе чисел в дополнительном коде в ЦАП путем прибавления 128 сдвигают этот диапазон до отрезка 0…255. Числа большие 128 при этом считаются положительными, а числа меньшие 128, – отрицательными. Среднее значение 128 соответствует нулю. Такое представление чисел, имеющих знак, через положительные числа называют сдвигом двоичного представления. Прибавление 128 можно очень просто связать с отрицанием знакового разряда. В общем случае для n-разрядного ЦАП отрицается старший (знаковый) разряд a_n-1.

Чтобы после этого получить при цифро-аналоговом преобразовании выходное напряжение с п

Дата добавления: 2014-01-20