Метод зон Френеля

Метод зон Френеля и его применение для объяснения дифракционных явлений

На основе результатов исследований Френеля удалось создать стройную волновую теорию, опираясь на которую ученый смог объяснить многие световые явления (отражение и преломление, интерференцию и дифракцию, двулучепреломление, поляризацию и поперечный характер световых волн). В волновой теории им дана новая формулировка принципа Гюйгенса и развит метод зон, тем самым превращен геометрический принцип в физический. Познакомимся с этим методом подробнее.

Пусть А – точечный источник света, С’C’’ – круглое отверстие в непрозрачном экране, находящееся на расстоянии R от источника (рисунок 13.1). Через это отверстие пройдет лишь часть фронта сферической волны, исходящей из точки А.

Определим действие этой волны в точке A’, расположенной на прямой AA’, проходящей через центр отверстия С’C’’, на расстоянии r_o от отверстия.

Для этого мысленно разделим волновой фронт на кольцевые зоны (зоны Френеля), построенные таким образом, чтобы расстояния от краев соседних зон до точки Р отличались на половину длины волны. Тогда волны, приходящие в точку Р от соответствующих частей соседних зон, будут иметь разность хода , то есть придут в точку Р в противоположных фазах.

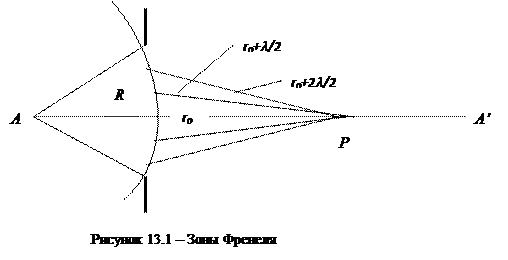
Амплитуда колебаний, обусловленных в точке Р отдельной зоной, зависит от площади зоны, от расстояния r от зоны до точки Р и от угла между отрезком r и нормалью к поверхности зоны.

Покажем, прежде всего, что площади зон примерно одинаковы.

Обозначим через 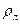радиус k –й зоны. Из чертежа (рисунок 13.2) ясно, что

,

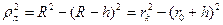откуда получаем:

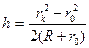. (13.1)

Так как расстояние до k –й зоны r_k на kl/2 больше расстояния r₀, то

,

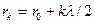и

.

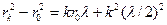Считая, что длина волны значительно меньше расстояния r₀, приближенно получим

,

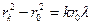после чего выражение (13.1) для h примет вид:

. (13.2)

Площадь поверхности сферического сегмента радиус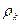а равна

.

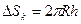С учетом выражения (13.2) получим:

.

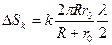В пределах k -го сегмента умещается k кольцевых зон. Поэтому площадь одной зоны может быть представлена как разность площади этого сегмента и сегмента, охватывающего k-1 зону:

. (13.3)

Таким образом, в рассматриваемом приближении площадь зоны не зависит от ее номера, то есть площади всех зон приблизительно одинаковы. Следовательно, амплитуды волн, доходящих до точки наблюдения Р, зависят только от расстояния r_k и от угла, составленного направлением этого отрезка с нормалью к поверхности зоны. С увеличением номера зоны расстояние r_k и угол наклона возрастают, поэтому амплитуды колебаний, обусловленных в точке Р отдельными зонами, должны монотонно убывать с ростом номера зоны:

.

Так как фазы колебаний, обусловленных в точке Р соседними зонами, противоположны, то амплитуда A_k суммарного колебания, обусловленного действием k зон, равна

,

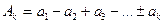где знак последнего слагаемого положителен при нечетном k и отрицателен при четном k. При нечетном числе зон

амплитуда результирующего колебания выше, чем при четном числе зон, укладывающихся в отверстии.

Учитывая монотонность убывания с ростом номера зоны амплитуды колебаний, обусловленных отдельными зонами, можно доказать справедливость приближенного равенства

,

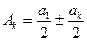где знак + соответствует нечетному числу зон, а знак «−» − четному числу зон.

Число зон, которое уложится на части волнового фронта, не закрытой экраном, зависит от отношения размеров отверстия к длине волны и от места его положения. Считая и пренебрегая величиной 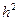, легко найти радиус кольцевой зоны:

. (13.4)

Очевидно, что этим выражением определяется и радиус отверстия, открывающего часть волнового фронта. Отсюда находим число зон, умещающихся в отверстии:

. (13.5)

Если фронт падающей волны плоский, то

, (13.6)

где 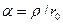− угол, под которым видно отверстие в экране из точки Р.

Таким образом, свет не распространяется через отверстие прямолинейно; освещенность в точке Р определяется размером и положением отверстия; она определяется действием всех точечных источников, лежащих на открытой части волнового фронта.

Если закрыть все четные (или все нечетные) зоны, оставляя открытыми все нечетные (четные) зоны, то в точке наблюдения интенсивность будет возрастать, так как в ней будут интерферировать волны, приходящие в одинаковой фазе (точнее, их фаза будет отличаться на целое число величин 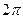). Устройства, с использованием которых удается выполнить такую операцию, называют зонными пластинками Френеля.

Дата добавления: 2014-01-20