Применение метода зон Френеля для объяснения дифракционных явлений

В научных изысканиях Френеля особое место занимают эксперименты по интерференции и дифракции света. Опираясь на эти эксперименты, он или подтверждал отдельные теоретические положения и следствия волновой теории, или обнаруживал новые.

В эксперименте по дифракции света в качестве точечного источника света он использует шарик из мёда, помещенный в небольшом отверстии медного листа. Проходящий от источника через «медовую линзу» свет освещал проволочку из железа. На экране возникала четкая дифракционная картина.

Ученый нарисовал картину волнового интерференционного поля и показал, что дифракционные полосы являются результатом интерференции лучей. К принципу интерференции Френель пришел независимо от Юнга.

Дифракционные явления Френеля наблюдают в непараллельных (сходящихся) лучах – точка наблюдения дифракционной картины лежит на оптической оси. Дифракцию Френеля можно наблюдать при прохождении света через круглое отверстие 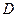в непрозрачном экране 1 (рисунок 13.3, а), при огибании контуров круглого непрозрачного экрана Э (рисунок 13.3,б), у края плоского непрозрачного экрана (рисунок 13.3,в).

Дадим качественное объяснение образованию дифракционной картины на круглом отверстии (рисунок 13.3, а). Разобьем отверстие на зоны таким образом, чтобы расстояния от краев каждой зоны до точки наблюдения отличались на половину длины волны. Световая волна проходит через отверстие 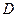в экране и в результате интерференции дифрагировавших волн в плоскости, проходящей через точку наблюдения перпендикулярно к оси симметрии оптической системы, образуется дифракционная картина, которая имеет вид концентрических темных и светлых колец. При нечетном числе зон, видимых из точки в отверстии, в центре дифракционной картины получается светлый кружок, за которым располагаются чередующиеся темные и светлые концентрические кольца. Яркость этих колец от центра к краям постепенно убывает (рис. 4.1,б). Если из точки наблюдения в отверстии открывается четное число зон, пятно в центре дифракционной картины темное.

В 1817 году Парижская Академия объявила конкурс научных работ по решению задач о дифракции света. Высокую оценку получила работа Френеля. При обсуждении этой работы специальной комиссией известный французский ученый С. Пуассон решил воспользоваться методом Гюйгенса – Френеля и рассмотреть теорию дифракции на круглом непрозрачном экране. Араго вспоминает: “Один из членов нашей комиссии – г-н Пуассон – вывел из сообщенных автором интегралов тот удивительный результат, что центр тени от круглого непрозрачного экрана должен быть таким же освещенным, как и в том случае, если бы экран не существовал, − это при условии, что лучи проникают в тень под малыми углами падения. Это заключение было проверено прямыми опытами, и наблюдение полностью подтвердило данные вычисления”.

Эксперимент по проверке расчетов Пуассона заключался в следующем (рисунок 13.3, б). От точечного источника на непрозрачный круглый небольшого размера диск направлялся узкий световой пучок. В результате дифракции света на этом диске на экране образовывалась дифракционная картина. В центре геометрической тени экрана действительно наблюдалось светлое пятно. Таким образом, эксперимент Френеля – Араго по проверке расчетов Пуассона явился убедительным доказательством справедливости волновой теории Френеля.

При дифракции на малом круглом экране (рисунок 13.3, б) в центре геометрической тени (в центре дифракционной картины) всегда получается светлое пятно (пятно Пуассона). Вклады зон в светлое поле в точке наблюдения пропорциональны площадям зон и медленно убывают с ростом номера зоны. Волны из соседних зон приходят в точку наблюдения с фазовым смещением, равным , и поэтому ослабляют друг друга. Наибольшим оказывается вклад первой зоны, расположенной непосредственно у края экрана.

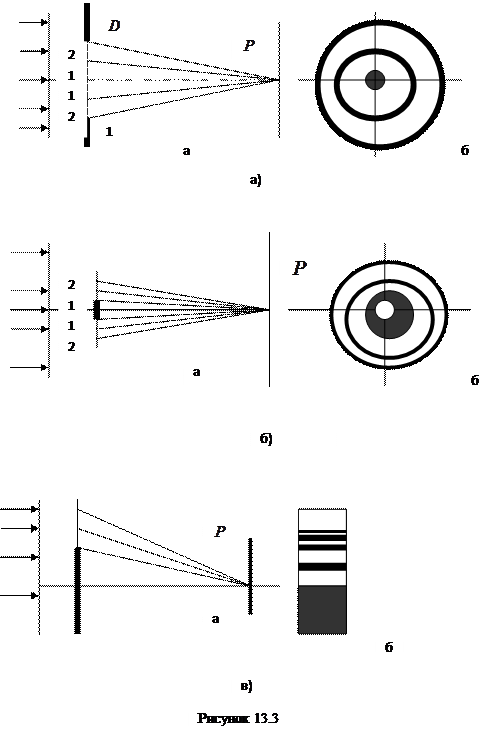
Если отверстие в непрозрачном экране представляет собой узкую прямоугольную щель, то её можно разделить на зоны, имеющие вид прямоугольных полосок, параллельных щели. В этом случае в плоскости наблюдения дифракционная картина будет представлять собой систему чередующихся светлых и черных полос с убывающей интенсивностью от центра к краям (рисунок 13.3, в).

13.3 Графическое определение амплитуд при дифракции; спираль Корню Изучить самостоятельно по учебному пособию: Ландсберг Г.С. Оптика.

Дата добавления: 2014-01-20