Сведение задачи к другой задаче

Один из способов решения задач состоит в том, чтобы свести, или редуцировать, одну задачу к другой. Тогда алгоритм решения второй задачи можно преобразовать таким образом, чтобы он решал первую. Если преобразование выполняется за полиномиальное время и вторая задача решается за полиномиальное время, то и наша новая задача так же решается за полиномиальное время.

Понятие полиномиальной сводимости:

Определение 2. Будем говорить, что задача Q сводится к задаче Р за полиномиальное время, если существует детерминированный полиномиальный алгоритм, преобразующий произвольный частный случай задачи Q в некоторый частный случай задачи Р, и второй полиномиальный алгоритм, преобразующий решение задачи Р в решение задачи Q.

Рассмотрим пример. Пусть требуется решить систему линейных уравнений 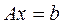с квадратной матрицей 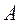размером n*n, имеющей отличный от нуля определитель 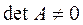. Это задача Q с исходными данными 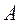и b. Вторая задача (Р) формулируется следующим образом: дана квадратная матрица 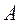; требуется найти обратную матрицу .

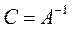Задача Q полиномиально сводится к задаче Р.

Проблема Р =NP?

Очевидно, что любая задача, принадлежащая классу Р, принадлежит и классу NP, т. к. она может быть полиномиально проверена, при этом задача проверки решения может состоять просто в повторном решении задачи.

Разница между классом Р и классом NP в том, что в первом случае у нас имеется детерминированный алгоритм, решающий задачу за полиномиальное время, а во втором мы такого алгоритма не знаем.

После введения в теорию алгоритмов понятий сложностных классов Эдмондсом (Edmonds, 1965), была сформулирована основная проблема теории сложности - Р =NP?, и высказана гипотеза о несовпадении этих классов. Словесно проблему можно сформулировать следующим образом: можно ли все задачи, решение которых проверяется с полиномиальной сложностью, решить за полиномиальное время?

На сегодня отсутствуют теоретические доказательства как совпадения этих классов (Р =NP), так и их несовпадения. Предположение состоит в том, что класс Р является собственным подмножеством класса NP, т. е. множество задач NP Р не пусто. Это предположение опирается на существование еще одного класса, а именно класс NР-полных задач.

Дата добавления: 2014-01-20