Тема 7. “ Условия равновесия системы сил. Эквивалентные системы”

Лекции № 14 – 15

§ 1. Принцип возможных перемещений

(Теорема Лагранжа – Остроградского)

Для идеальных связей можно получить условие равновесия, содержащее только активные силы.

Теорема Лагранжа-Остроградского. Необходимым и достаточным условием равновесия сил, приложенных к системе материальных точек, на которую наложены идеальные и стационарные связи, является равенство нулю суммы возможных работ всех активных сил:

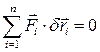(7.1)

Если на систему наложены неидеальные связи, то для применения принципа возможных перемещений, в соответствии с принципом освобождаемости, их следует отбросить, присоединив реакции таких связей к активным силам.

При решении задач с помощью принципа возможных перемещений удобно придерживаться следующего порядка действий:

1. Если на систему материальных точек наложены неидеальные связи, то они отбрасываются, а реакции этих связей присоединяются к активным силам.

2. Устанавливается непосредственно число степеней свободы рассматриваемой системы материальных точек. Для этого возможные перемещения всех точек, к которым приложены активные силы, выражаются через возможные приращения независимых параметров, однозначно определяющих положения всех точек системы. Число таких независимых параметров равно числу степеней свободы системы.

3. На основании принципа возможных перемещений приравнивается нулю сумма возможных работ активных сил, либо сумма возможных мощностей системы сил. (Если система материальных точек есть твердое тело, то внутренние силы не учитываются, поскольку сумма возможных работ внутренних сил равна нулю)

4. Так как возможные приращения независимых параметров произвольны, то суммы коэффициентов при этих приращениях вравенстве, выражающем принцип возможных перемещении, равны нулю. Таким образом, получается система уравнений, число которых равно числу степеней свободы системы.

5. Находятся неизвестные из полученной системы уравнений.

Пример 1. Три груза, веса которых P₁, Р₂ и Р изображены на чертеже (рис. 87). Они соединены между собой нерастяжимым и невесомым тросом, перекинутым через два соосных блока с неподвижной осью, проходящей через точку О и через блок с осью в точке О.

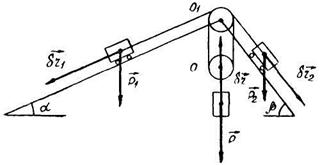Рис. 87

Пренебрегая трением и весом подвижного блока, найти из условии равновесия веса P1 и Р2, считая, что углы a и b заданы. Решение. Возможные перемещения , и 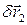грузов на наклонных плоскостях независимы и эти перемещения однозначно определяют возможное перемещение третьего груза.

Поскольку каждый из первых двух грузов имеет одну степень свободы, то, следовательно, система имеет две степени свободы. Для указанных на чертеже направлений векторов и 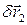после элементарного кинематического анализа получим

.

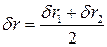На основе принципа возможных перемещений запишем

.

Подставляя в это равенство значение 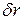, и полагая (в силу не зависимости и 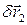это можно сделать) , получим

.

Если положить , то

.

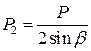Дата добавления: 2014-01-20