Пример

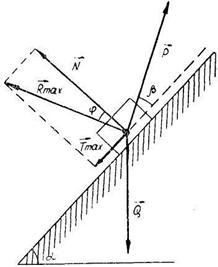Рис. 82

На наклонной плоскости, образующей с горизонтом угол a, находится тело весом (рис. 82). Определить: а) наименьшее значение силы , составляющей угол b с наклонной плоскостью и способной сдвинуть тело вверх; б) значение угла b, при котором эта сила будет минимальной. Какое при этом давление будет оказывать тело на плоскость? Коэффициент трения тела оплоскость равен 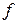. Решение. Для решения задачи воспользуемся теоремой о трех силах.

Теорема о трех силах. Если система трех сил находится в равновесии, то линии действия этих сил лежат в одной плоскости и либо пересекаются в одной точке, либо параллельны.

Так как три силы – сила тяжести , сила и реакция плоскости находятся в равновесии, то согласно теореме о трех силах линии действия этих сил должны лежать в одной плоскости и либо являться параллельными прямыми, либо пересекаться в одной точке. Первый случай, очевидно, исключается, так как по условию задачи линии действия сил и не могут быть параллельными.

В дальнейшем будет указано, что условием равновесия систе­мы сил, линии действия которых пересекаются в одной точке (сходящейся системы сил), является равенство нулю главного вектора системы сил. В соответствии с условием данной задачи это значит, что

т. е. треугольник, построенный на векторах сил , и , должен быть замкнут. Построим этот треугольник для предельного случая, когда величина силы трения максимальна и, следовательно, реакция образует с нормальной составляющей 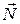угол трения φ. В выбранном масштабе из произвольной точки строим вектор силы тяжести и через конец этого вектора проводим прямую, коллинеарную реакции .

Легко видеть, что эта прямая образует с вектором угол (a+φ). Если провести через начало вектора прямую, составляющую с ним угол (это угол между векторами и ), то будет построен силовой треугольник (рис. 83), из которого определяется величина силы .

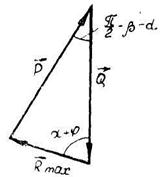Рис. 83

Используя теорему синусов, находим , откуда .

Наименьшее значение силы Р получается при b = φ. Имеем

.

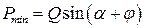Напомним, что . После несложных вычислений получим:

Величина силы давления тела на плоскость равна величине нормальной реакции. В предельном случае

.

Трение качения. Если рассматриваемое тело имеет форму катка и под действием приложенных активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте соприкосновения могут возникнуть силы реакции, препятствующие не только скольжению, но и качению. Примерами таких катков являются различные колеса, как, например, у электровозов, вагонов, автомашин, шарики и ролики в шариковых и роликовых подшипниках и т. п.

Пусть цилиндрический каток находится на горизонтальной плоскости под действием активных сил. Соприкосновение катка с плоскостью из-за деформации фактически происходит не вдоль одной образующей, как в случае абсолютно твердых тел, а по некоторой площадке. Если активные силы приложены симметрично относительно среднего сечения катка, т. е. вызывают одинаковые деформации вдоль всей его образующей, то можно изучать только одно среднее сечение катка.

Рис. 84

Активные силы, действующие на катки в виде колес (рис. 84). кроме силы тяжести обычно состоят из силы , приложенной к центру колеса параллельно общей касательной в точке А, и пары сил с моментом L, стремящейся катить колесо, называемое в этом случае ведомо-ведущим. Если L = 0, а Q ≠ 0, то колесо называют ведомым; если L ≠ 0, a Q= 0, то ведущим. Ведомо-ведущими являются колеса локомотива, идущего вторым в составе поезда.

Если активные силы, действующие на колесо, привести к точке А соприкосновения катка с плоскостью, у которых нет деформации, то в общем случае получим силу и пару сил, стремящиеся заставить каток скользить и катиться. Следует различать чистое качение, когда точка соприкосновения А катка не скользит по неподвижной плоскости, и качение со скольжением, когда наряду с вращением катка есть и скольжение, т.е. точка А катка движется по плоскости. При чистом скольжении, наоборот, каток движется по плоскости, не имея вращения.

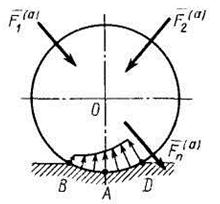Рис. 85

Рис. 86

Соприкосновение среднего сечения колеса с неподвижной плоскостью из-за деформации колеса и плоскости происходит по некоторой линии BD. По этой линии на колесо действуют распределенные силы реакции (рис. 85). Если привести распределенные силы к точке А, то в этой точке получим главный вектор этих распределенных сил с составляющими 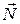(нормальная реакция) и (сила трения скольжения), а также пару сил с моментом М. При симметричном распределении сил по линии BD относительно точки А момент М пары сил равен нулю. В этом случае нет активных сил, стремящихся катить каток в каком-либо направлении.

Приведем активные силы 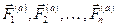,в общем случае, к точке А. В этой точке получим главный вектор этих сил 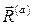и пару сил, момент которой равен главному моменту L (рис. 86).

При равновесии катка, т. е. когда каток не катится и не скользит по плоскости, активные силы уравновешиваются силами реакций связи и, следовательно,

.

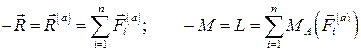Изменим активные силы, приложенные к катку так, чтобы увеличивался момент L пары активных сил, стремящейся катить каток. Пока каток находится в равновесии, увеличивается и равный ему по числовой величине, но противоположный по направлению момент М пары сил, препятствующий качению катка и возникающий от действия на каток неподвижной плоскости. Наибольшее значение М достигается в момент начала качения катка по плоскости.

Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:

1. Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка.

2. Предельное значение момента М_тах пропорционально нормальному давлению, а следовательно, и равной ему нормальной реакции :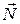

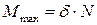. (6.14)

Коэффициент пропорциональности δ называют коэффициентом трения качения при покое или коэффициентом трения второго рода. Из формулы (6.14) следует, что δ имеет размерность длины.

3. Коэффициент трения качения δ зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости. Для случая качения вагонного колеса по стальному рельсу коэффициент трения качения δ ≈ 0,5 мм.

Законы трения качения, как и законы трения скольжения, справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся материалов катка и плоскости.

Дата добавления: 2014-01-20