
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 6. “ Основные понятия и аксиомы статики”
|
|
|
|
Лекция № 13
§ 1. Несвободные системы материальных точек. Элементарная работа силы и системы сил.
На систему материальных точек действуют силы внешние и внутренние.
Определение. Внешними называются силы, с которыми точки либо тела, не входящие в рассматриваемую систему, действуют на точки, входящие в нее. Внутренними силами называются силы взаимодействия точек рассматриваемой системы.
Система внутренних сил, приложенных к рассматриваемой системе материальных точек, в соответствии с третьим законом Ньютона, состоит из двоек сил. Главный вектор и главный момент системы внутренних сил равны нулю.
Пусть равнодействующая внутренних сил, приложенных к k–ой точке системы, обозначена 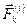 , главный вектор и главный момент системы внутренних сил – соответственно
, главный вектор и главный момент системы внутренних сил – соответственно 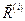 и
и 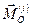 .
.
Тогда 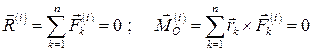 .
.
Для случая, когда любая система сил, приложенных к твердому телу, плоская или пространственная, приводится к равнодействующей силе, часто применяют теорему Вариньонa: Если система сил имеет равнодействующую, то вектор равнодействующей равен главному вектору системы сил, а момент равнодействующей относительно точки (или оси) равен главному моменту системы сил относительно этой точки (оси).
В механике часто встречаются задачи, в которых на возможные движения системы материальных точек наложены некоторые ограничения.
Определение. Материальная точка называется свободной, если она может занимать любое положение в некоторой области, имея в этом положении произвольную скорость. Система материальных точек называется свободной, если все точки системы одновременно свободны.
Тела, ограничивающие перемещения точек системы, называются с в я – з я м и. Если на точки системы наложена некоторая связь, то это значит, что координаты точек системы, проекции скоростей точек и время связаны некоторыми функциональными зависимостями:
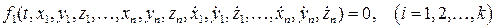 (6.6)
(6.6)
Уравнения (6.6) называются уравнениями связей.
Определение. Система материальных точек, на которую наложена по крайней мере одна связь, называется несвободной.
Определение. Связь называется стационарной, если в уравнение связи время явно не входит. В противном случае связь называется нестационарной.
Определение. Связь называется голономной, если уравнение связи не содержит проекций скоростей точек системы, если в уравнение связи проекции скоростей входят в не интегрируемой комбинации, то связь называется неголономной.
В дальнейшем будем рассматривать только стационарные, голономные связи.
Если существует такое положение системы, что координаты точек системы удовлетворяют всем уравнениям связей, то связи называются непротиворечивыми.
Если при каком-то движении системы координаты ее точек удовлетворяют некоторым условиям связи и отсюда следует, что будут удовлетворены и оставшиеся уравнения связи, то связи называются зависимыми. В противном случае связи называются независимыми.
Рассмотрим только непротиворечивые и независимые связи, число которых меньше числа координат точек системы.
Итак, рассматривается система связей
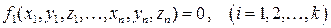 (6.7)
(6.7)
Число s =3n – k называется числом степеней свободы системы.
Скорости точек системы удовлетворяют уравнениям:
 , (6.8)
, (6.8)
где  – вектор с проекциями
– вектор с проекциями 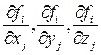 .
.
Каждая совокупность векторов  , удовлетворяющая уравнениям (6.8), называется возможными скоростями точек системы. Эти векторы имеют размерности скоростей. Истинные скорости точек системы есть некоторые возможные.
, удовлетворяющая уравнениям (6.8), называется возможными скоростями точек системы. Эти векторы имеют размерности скоростей. Истинные скорости точек системы есть некоторые возможные.
Векторы  , где
, где  – возможные скорости, а a – произвольное вещественное число, называются возможными перемещениями.
– возможные скорости, а a – произвольное вещественное число, называются возможными перемещениями.
Элементарные перемещения это некоторые возможные.
Чтобы убедиться в этом, достаточно взять в качестве возможных скоростей истинные, и положить a= dt.
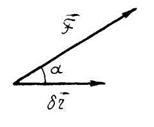 Рис. 79
Рис. 79
| Определение. Возможной работой силы  называется скалярное произведение вектора силы называется скалярное произведение вектора силы 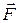 на возможное перемещение точки ее приложения на возможное перемещение точки ее приложения  (рис. 79): (рис. 79):
 (6.9) (6.9)
|
Определение. Возможной мощностью силы называется скалярное произведение вектора силы и возможной скорости точки ее приложения:
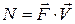 (6.10)
(6.10)
Возможная мощность системы сил, приложенных к твердому телу, равна
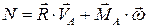 (6.11)
(6.11)
где  и
и 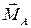 – соответственно главный вектор и главный момент системы сил;
– соответственно главный вектор и главный момент системы сил;
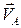 и
и 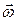 – соответственно возможная скорость точки А тела и его возможная угловая скорость.
– соответственно возможная скорость точки А тела и его возможная угловая скорость.
Формуле (6.11) соответствует следующее выражение для возможной работы системы сил, приложенных к твердому телу:
 , (6.12)
, (6.12)
где 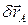 и
и 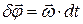 – соответственно возможное перемещение точки А тела и его возможный вектор поворота.
– соответственно возможное перемещение точки А тела и его возможный вектор поворота.
Если рассматривается мгновенно-поступательное движение твердого тела, то
 ,
,
где  – возможное перемещение любой точки тела;
– возможное перемещение любой точки тела;
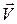 – ее возможная скорость.
– ее возможная скорость.
Если тело совершает мгновенное вращение, то
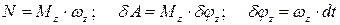
где 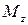 – главный момент системы сил относительно мгновенной оси;
– главный момент системы сил относительно мгновенной оси;
 – проекция возможной угловой скорости на мгновенную ось.
– проекция возможной угловой скорости на мгновенную ось.
Т.к. для системы внутренних сил главным вектор и главный момент, вычисленный относительно произвольного полюса, равны нулю, то из равенства (6.11) следует, что возможная мощность, а следовательно, и возможная работа
системы внутренних сил, приложенных к твердому телу, равны нулю:

Определение. Силы, с которыми рассматриваемая система материальных точек действует на связи, называются силами давления на связи; силы, с которыми связи действуют на рассматриваемую систему материальных точек, называются реакциями связей.
Сила давления на связь и соответствующая реакция связи подчиняются третьему закону Ньютона, т. е. они имеют общую линию действия и векторы этих сил отличаются только знаком. В отличие от реакций заданные силы называются активными.
Определение. Связи называются идеальными, если сумма возможных работ реакций связей равна нулю, т. е.
 ,
,
где 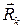 – реакция, приложенная к k-ой точке;
– реакция, приложенная к k-ой точке;
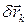 – возможное перемещение k-ой точки.
– возможное перемещение k-ой точки.
§ 2. Реакции связей.
Реакции связей, как правило, неизвестны и определяются в случае покоя твердого тела из условий равновесия системы сил, действующих на тело. При этом в механике несвободные тела часто рассматриваются как свободные. При таком рассмотрении используется принцип освобождаемости: каждая связь может быть отброшена, если реакцию этой связи перевести в класс активных сил.
В ряде случаев бывает заранее известна точка приложения реакции. Это имеет место, например, в том случае, если можно считать, что рассматриваемое твердое тело и связь, на него наложенная, соприкасаются в одной точке (это означает, что размеры площадки соприкосновения тела и связи малы по сравнению с характерными размерами задачи).
Существуют связи, для которых направление реакции тоже заранее известно. Такие связи называются о п р е д е л е н н ы м и. В большинстве случаев совокупность реакций данной связи представляет собой сложную систему сил. В таком случае не ставится задача отыскания каждой силы этой системы, а предполагается, что совокупность реакций данной связи приведена к простейшему виду и отыскивается эта простейшая система, сил. С такими случаями мы сталкиваемся, когда рассматриваемое тело и связь соприкасаются на конечной части своих поверхностей.
Будем называть связи опорами. Рассмотрим основные типы опор и их реакции.
| Тип опоры | Схема связи | Направление реакции | |
| 1. Гладкая поверхность (хорошо отполированная поверхность) | 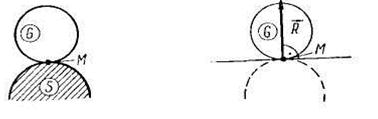
| Реакция гладкой поверхности направлена по нормали к поверхности. | |
| 2. Опора на каток (подвижный шарнир) | 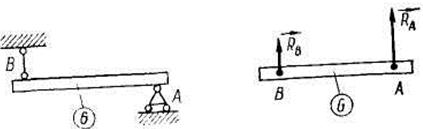
| Реакция опоры на каток перпендикулярна поверхности, по которой перемещается каток. | |
| 3. Опора на острие | 
| Реакция опоры на острие направлена перпендикулярно той поверхности, к которой однозначно проводится касательная. | |
4. Неподвижный цилиндрический шарнир (подшипник)
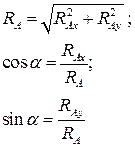
| 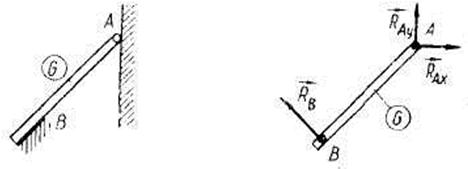
| Устраняет поступательное движение конца конструкции в любом направлении. Реакция лежит в плоскости перпендикулярной оси шарнира и неизвестна по направлению. Её раскладывают на две составляющие по выбранным осям координат. | |
| 5. Сферический шарнир (подпятник) | 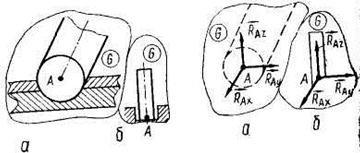
| Реакция шарнира – диагональ параллелепипеда. | |
| 6. Жесткая заделка или защемление | на плоскости 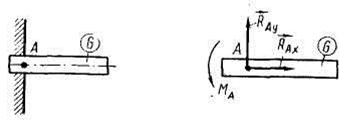 в пространстве
в пространстве
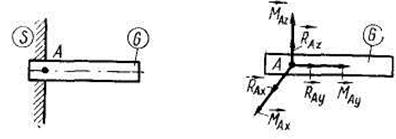
| Такое закрепление не допускает на линейных ни угловых перемещений опорного сечения.
Реакции 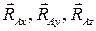 не дают сдвинуть точку закрепления, а моменты пар сил не дают сдвинуть точку закрепления, а моменты пар сил  исключают поворот опорного сечения. исключают поворот опорного сечения.
| |
| 7. Гибкая связь (закрепление нитями, тросами, цепями и др.) | 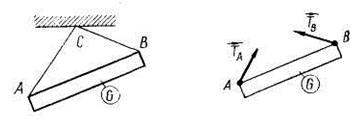
| Реакция нити направлена по нити. |
| 8. Идеальный стержень | 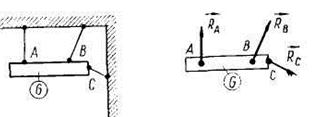
| Если вместо нитей тело подвешено на идеальных жестких стержнях, то реакция стержня направлена вдоль стержня. Определение. Идеальным называется невесомый стержень, шарнирно закрепленный с двух сторон. |
| 9. Шероховатая поверхность | 
| Реакцию шероховатой поверхности раскладывают на две составляющие: нормальную и силу трения.
Согласно закона Кулона, сила трения равна 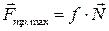 ,
где f – коэффициент трения. ,
где f – коэффициент трения.
|
§ 3. Трение.
Наряду с идеальными связями, могут быть связи неидеальные. К числу последних относятся связи с трением. Рассмотрим некоторые законы трения.
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения возникает сила трения скольжения.
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает пара сил, препятствующая качению катка. Возникновение силы трения, препятствующей скольжению, иногда называют трением первого рода, а возникновение пары сил, препятствующей качению, – трением второго рода.
Трение скольжения. Пусть на тело действует плоская система активных сил, и тело находится в равновесии, соприкасаясь с поверхностью другого тела, являющегося связью для рассматриваемого тела. Если поверхности соприкасающихся тел абсолютно гладкие и тела абсолютно твердые, то реакция поверхности связи направлена по нормали к общей касательной в точке соприкосновения и направление реакции в этом случае не зависит от действующих на тело активных сил. От активных сил зависит только числовое значение силы реакции. В действительности абсолютно гладких поверхностей и абсолютно твердых тел не бывает. Все поверхности тел в той или иной степени шероховаты и все тела деформируемы. В связи с этим и сила реакции  шероховатой поверхности при равновесии тела зависит от активных сил не только по модулю, но и по направлению (рис. 80).
шероховатой поверхности при равновесии тела зависит от активных сил не только по модулю, но и по направлению (рис. 80).
 Рис.80
Рис.80
| Если силу реакции  шероховатой поверхности разложить на составляющие, одна из которых ( шероховатой поверхности разложить на составляющие, одна из которых (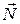 ) направлена по общей нормали к поверхности соприкосновения, а другая ( ) направлена по общей нормали к поверхности соприкосновения, а другая (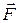 ) находится в касательной плоскости к этим поверхностям, то составляющая ) находится в касательной плоскости к этим поверхностям, то составляющая 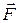 силы реакции является силой трения скольжения, а составляющая силы реакции является силой трения скольжения, а составляющая 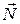 – нормальной реакцией. – нормальной реакцией.
|
Итак, силой трения называют составляющую реакции поверхности, лежащую в касательной плоскости к ней.
В теоретической механике обычно рассматривается только сухое трение между поверхностями тел, т.е. такое трение, когда между ними нет смазывающего вещества. Для сухого трения надо различать трение скольжения при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.
Еслитело, лежащее на шероховатой горизонтальной плоскости (рис. 81) находится в покое под действием трех сил: горизонтальной силы 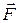 , силы тяжести
, силы тяжести  и реакции плоскости
и реакции плоскости  , то из равенства нулю главного вектора следует, что векторы составляющих реакции удовлетворяют условиям:
, то из равенства нулю главного вектора следует, что векторы составляющих реакции удовлетворяют условиям:
 Рис.81
Рис.81
| 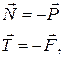 где
где 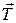 – сила трения.
Из второго равенства следуют важные выводы:
а) сила трения всегда направлена в сторону, противоположную предполагаемому движению;
б) величина силы трения в случае, если тело находится в покое, равна величине составляющей активной силы, лежащей в касательной плоскости к поверхности. – сила трения.
Из второго равенства следуют важные выводы:
а) сила трения всегда направлена в сторону, противоположную предполагаемому движению;
б) величина силы трения в случае, если тело находится в покое, равна величине составляющей активной силы, лежащей в касательной плоскости к поверхности.
|
Если неограниченно увеличивать силу 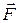 , то при некотором значении величины
, то при некотором значении величины 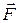 тело начинает двигаться, т. е. ветчина силы трения уже не будет равна
тело начинает двигаться, т. е. ветчина силы трения уже не будет равна 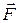 . Опыты показывают, что величина силы трения имеет верхний предел, зависящий от величины нормальной реакции и материалов соприкасающихся тел.
. Опыты показывают, что величина силы трения имеет верхний предел, зависящий от величины нормальной реакции и материалов соприкасающихся тел.
Ш. Кулон экспериментально нашел это максимальное значение величины силы трения и в 1781 г. сформулировал результаты своих экспериментов в форме закона.
Закон Кулона. Максимальная сила трения пропорциональна величине нормальной реакции:
 , (6.13)
, (6.13)
либо
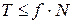 .
.
Коэффициент 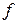 называют коэффициентом трения скольжения. Кулон установил, что коэффициент трения зависит лишь от материала соприкасающихся тел и степени обработки их поверхности. Хотя последующие более точные эксперименты показали, что этот коэффициент также несколько зависит и от времени соприкосновения тел и от площади соприкосновения, мы не допустим значительной ошибки, придерживаясь взглядов Кулона.
называют коэффициентом трения скольжения. Кулон установил, что коэффициент трения зависит лишь от материала соприкасающихся тел и степени обработки их поверхности. Хотя последующие более точные эксперименты показали, что этот коэффициент также несколько зависит и от времени соприкосновения тел и от площади соприкосновения, мы не допустим значительной ошибки, придерживаясь взглядов Кулона.
Углом трения φ называют угол, тангенс которого равен коэффициенту трения. Конусом трения называют конус, ось которого совпадает с нормалью к поверхности, а угол образующей с осью равен углу трения (рис. 81). Угол a, который реакция составляет с нормалью к поверхности, удовлетворяет условию
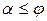 ,
,
т. е. угол отклонения реакции от нормали к поверхности при покое не превосходит угла трения. Если  ,то сила трения достигает максимального значения. В этом случае, который называется предельным, возможен и покой тела и его движение.
,то сила трения достигает максимального значения. В этом случае, который называется предельным, возможен и покой тела и его движение.
Приведенная ниже теорема дает удобный критерий покоя тела на шероховатой поверхности.
Теорема. Необходимым и достаточным условием покоя точки на шероховатой поверхности является требование, чтобы линия действия активной силы проходила внутри конуса трения, либо совпадала с его образующей (в последнем случае покой тела будет лишь тогда, когда тело будет находиться в покое и в начальным момент времени).
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 511; Нарушение авторских прав?; Мы поможем в написании вашей работы!