Тема 4. “ Сложное движение точки и тела”

Лекция № 10.

§ 1. Абсолютное, относительное и переносное движения точки. Теорема о сложении скоростей.

Основные понятия абсолютного, относительного и переносного движений точки были нами введены в теме № 2, § 3 (лекция 4). Перейдём к формулировке и доказательству теоремы о сложении скоростей.

Рассмотрим лемму о локальной производной.

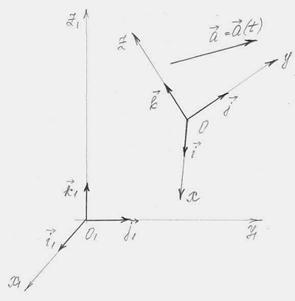Рис. 55

Пусть дана некоторая вектор–функция, заданная проекциями на неподвижную и подвижную системы отсчета: Для наблюдателей, связанных с системам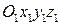и и 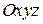, эта вектор–функция будет различной, а значит, и производная этой вектор–функции в каждой из этих систем отсчета будет разной.

Определение. Абсолютной производной вектор–функции назовем производную относительно абсолютной системы отсчета и обозначим её .

Определение. Локальной производной вектор–функции назовем производную относительно переносной системы отсчета и обозначим её .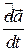

Установим связь между этими производными.

В подвижной системе отсчета . Локальная производная этой функции будет 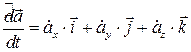, т. к. – постоянны в переносной системе отсчета.

Вычислим теперь абсолютную производную этой функции, помня, что теперь – переменные величины.

. (5.1)

Если подвижная система движется поступательно, – постоянные векторы, а значит 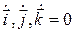. Тогда .

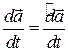Если подвижная система совершает плоскопараллельное движение, то для концов ортов системы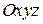можно записать соотношения:

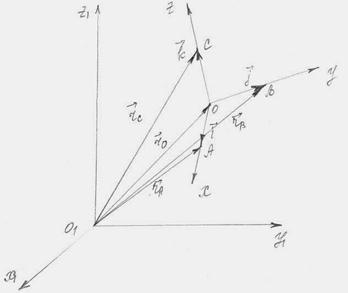Рис. 56

Из этих соотношений получим: Продифференцируем обе части последних равенств: (5.2)

но из формулы Эйлера для твердого тела имеем:

После подстановки последних выражений в (5.2), получим формулы Пуассона:

(5.3)

Подставим равенства (5.3) в (5.1):

(5.4)

Полученная формула называется формулой Бура, и выражает собой лемму о локальной производной:

Лемма. Абсолютная производная вектор–функции равна её локальной производной и векторному произведению угловой скорости переносящей среды на саму вектор–функцию.

Теорема. Абсолютная скорость точки равна сумме переносной и относительной скоростей.

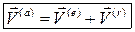(5.5)

Доказательство.

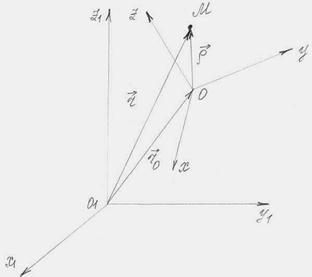Рис. 57

Из чертежа видно, что . Дифференцируем обе части этого равенства по времени: Согласно лемме о локальной производной: . Тогда (5.6)

Первые два слагаемых определяют, согласно формуле Эйлера, скорость той точки переносящей среды, с которой в данный момент совпала исследуемая точка М, а это по определению есть переносная скорость точки, т.е.

. (5.7)

Производная же 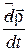определяет скорость точки относительно подвижной системы отсчета, т.е. относительную скорость точки:

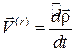. (5.8)

Таким образом, окончательно формула (5.6) примет вид . ■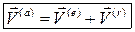

§2. Теорема Кориолиса о сложении ускорений.

Продифференцируем обе части равенства (5.5) в абсолютной системе отсчета:

Дата добавления: 2014-01-20