
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 1. “ Кинематика точки”
Курс «Техническая механика» включает в себя??? тем, охватывающих некоторые вопросы теоретической механики и теории машин и механизмов.
Начнем изучение курса с теоретической механики.
В В Е Д Е Н И Е
Первоначальный смысл слова механика — искусство, хитрость, ухищрение. Механиками называли искусника, изобретателя. Греческое слово mhcagh означало и машина и всякого рода ухищрение. Термин механика впервые был употреблен в III веке до нашей эры одним из учеников Аристотеля при изучении явлений, в которых «меньшее одолевает большее», как, например, при подъеме груза при помощи рычага. Древнегреческий философ и поэт Антифонт (2-я половина V века до нашей эры) говорил: «Посредством искусства мы одерживаем верх там, где побеждены природой». Так же переводили это слово древнерусские книжники.
 Возникновение механики уходит в глубокую древность. Уже задолго до нашей эры при постройке различных сооружений (египетские пирамиды, древние храмы) люди пользовались некоторыми эмпирическими знаниями по механике и применяли простейшие механические приспособления (рычаг, блок, наклонная плоскость). Однако переход от чисто эмпирических знаний к установлению общих законов механики не мог совершиться сразу, а потребовал весьма длительного времени, в течение которого накоплялся фактический материал в результате наблюдений и практической деятельности людей. Потребности земледелия, строительства, мореплавания и военного дела, необходимость точного взвешивания в связи с дальнейшим расцветом торговли – все это способствовало развитию механики.
Возникновение механики уходит в глубокую древность. Уже задолго до нашей эры при постройке различных сооружений (египетские пирамиды, древние храмы) люди пользовались некоторыми эмпирическими знаниями по механике и применяли простейшие механические приспособления (рычаг, блок, наклонная плоскость). Однако переход от чисто эмпирических знаний к установлению общих законов механики не мог совершиться сразу, а потребовал весьма длительного времени, в течение которого накоплялся фактический материал в результате наблюдений и практической деятельности людей. Потребности земледелия, строительства, мореплавания и военного дела, необходимость точного взвешивания в связи с дальнейшим расцветом торговли – все это способствовало развитию механики.
В первый период своего зарождения и становления механика, имевшая объектом своего изучения простейшие орудия и машины, развивалась, главным образом, в области статики – наиболее простого раздела механики, представляющего собой учение о силах и о покое тел. В древних трактатах по механике встречаются рассуждения о силе и ее свойствах (Аристотель, 384 – 322 гг. до н. э.). Основоположником статики является Архимед (287 – 212 гг. ю н. э.), который подытожил знания древних по статике и заложил ее научные основы. Архимед с искусством великого ученого и изобретателя применил свои, знания по механике в военном деле при защите своего родного города Сиракуз от римлян во время Второй Пунической войны.
Но в рабовладельческом обществе механика не могла успешно развиваться. Благодаря дешевому труду рабов, не было надобности в создании и применении машин, а поэтому отсутствовали предпосылки к быстрому развитию техники и механики.
Эпоха средних веков характеризуется в области механики, как и в области других наук, почти полным застоем, что объясняется характером общественных отношений при феодальном строе и господством теологии в области философии и естественных наук.
Только с эпохи Возрождения (вторая половина XV века), в связи с усилением роли торгового капитала, ремесла, мореплавания, военного дела, начинает быстро развиваться и механика. В эту эпоху следует отметить ряд исследований по механике знаменитых ученых Леонардо да Винчи (1462–1519) и Коперника (1473–1543). Крупнейшим вкладом в механику было открытие законов движения планет Иоганном Кеплером (1571 – 1630) как на основе собственных наблюдений, так и наблюдений Тихо Браге (1546 – 1601).
Основоположником важнейшего раздела механики – динамики является итальянский ученый Галилео Галилей (1564 – 1642), который в почти законченном виде сформулировал первый закон динамики – закон инерции – и решил ряд важных задач динамики. Важнейшие результаты теоретической механики при создании её основ не могли быть получены без создания нового математического аппарата – дифференциального и интегрального исчисления. Наряду и одновременно с Лейбницом этот аппарат был создан Исааком Ньютоном (1643 – 1727) – ученым, которому механика более всего обязана созданием важнейшего раздела – динамики. Для того чтобы по движению можно было судить о силах, Ньютон ввел понятие массы, дав определение массы как количества материи, отделив понятие массы от понятия веса, и тем самым на основе метафизико–материалистических представлений о материи ввел теоретическое понятие массы, отличное от эмпирического понятия веса. Благодаря такому определению массы, удалось поставить важнейший для механики вопрос о соотношении инертной и тяготеющей масс, так какмасса входила в два независимых друг от друга важнейших законов природы – второй закон Ньютона и закон всемирного тяготения. Как известно, понятие массы является важнейшим понятием, использующимся, кроме механики, в других физических теориях. Ньютон окончательно установил основные законы классической механики, сформулировав их в виде аксиом, основываясь на законах движения планет, открытых Кеплером, теоретически получил закон всемирного (ньютонианского) тяготения. Ньютону также принадлежит в теоретической механике основная аксиома в теории удара и большое количество важнейших результатов в области других наук.
В то же время статика получила свое дальнейшее развитие в работах Вариньона (1654 – 1722), который установил в окончательном виде понятие момента силы и рассмотрел ряд задач статики. Современную форму статике позже придал французский геометр Пуансо (1777 – 1859).
XVII век можно охарактеризовать как период создания основ динамики. К началу XVIII века динамика материальной точки получила свое почти законченное развитие. XVIII век характеризуется разработкой общих принципов механики и важнейшими исследованиями по механике твердого тела, гидродинамике и небесной механике. При этом развитие механики идет по пути создания и разработки аналитических методов, чему способствовало появление новых мощных методов математического анализа. Основоположниками аналитического направления следует считать Леонарда Эйлера (1707 – 1783), Иоганна Бернулли (1667 – 1748), Даниила Бернулли (1700 – 1782), Жана Лерона Даламбера (1717 – 1783).
Особенное развитие аналитические методы получили в работе выдающегося французского ученого Жозефа Луи Лагранжа (1736 – 1813). Лагранж всю механику изложил строго аналитически и получил общее уравнение динамики, исходя из которого может быть построена вся динамика, а также вывел в общем виде дифференциальное уравнение движения механической системы. Ему принадлежат также многочисленные работы: по механике сплошной среды.
Русским и советским ученым принадлежат крупнейшие открытия и приоритет во многих областях науки и, в частности, в области механики и теоретической механики. Общеизвестны работы крупнейших отечественных ученых: Михаила Васильевича Остроградского (1801 – 1861), Пафнутия Львовича Чебышева (1821 – 1894), Александра Михайловича Ляпунова (1857–1918), Софьи Васильевны Ковалевской (I860 – 1891), Ивана Всеволодовича Мещерского (1859 – 1935), Николая Егоровича Жуковского (1847 – 1921), Константина Эдуардовича Циолковского (18571 – 1935), Сергея Александровича Чаплыгина (1869–1942), Алексея Николаевича Крылова (1863 – 1945), Сергея Павловича Королева (1906 – 1966) и многих других.
По характеру решаемых задач механику разделяют на статику –учение о равновесии тел под действием сил, кинематику – учение о геометрических свойствах тел и динамику – учение о движении тел под действием сил. Наиболее важные проблемы механики относятся к динамике. Законы статики являются частным, случаем более общих законов динамики, поскольку равновесие есть частный случай движения. «Всякий покой, всякое равновесие только относительны, они имеют смысл только по отношению к той или иной определенной форме движения. Так, например, то или иное тело может находиться на Земле в состоянии механического равновесия, т. е. в механическом смысле – в состоянии покоя, но это нисколько не мешает тому, чтобы данное тело принимало участие в движении Земли и в движении всей солнечной системы, как это ничуть не мешает его мельчайшим физическим частицам совершать обусловленные его температурой колебания или же атомам его вещества – совершать тот или иной химический процесс» (Энгельс Ф. Диалектика природы).
При теоретических исследованиях в механике в качестве основных объектов рассматриваются материальная точка, абсолютно твердое тело и сплошная (непрерывная) среда. Каждому из этих абстрактных понятий соответствует представление о материальном теле, при изучении равновесия или движения которого можно соответственно пренебречь или его размерами, или его деформацией, или же его атомно–молекулярной структурой. В соответствии с этим механику разделяют на механику материальной точки и системы материальных точек, механику абсолютно твердого тела и механику сплошных сред. Последнюю, в свою очередь, подразделяют на: механику жидкостей и газов (гидромеханика, аэродинамика, газодинамика, магнитная гидродинамика), механику упруго и пластически деформируемых тел (теория упругости, теория пластичности, реология), механику сыпучих сред.
Предметом теоретической механики является изучение с помощью соответствующих математических методов наиболее общих законов механического движения и их приложения к рассмотрению движения материальной точки, системы материальных точек и абсолютно твердого тела. Как и другие науки о механическом движении, теоретическая механика подразделяется на статику, кинематику и динамику.
В теоретической механике рассматриваются также основные принципы, включая вариационные принципы механики, и, вытекающие из общих законов и принципов, уравнения и теоремы. К теоретической механике относятся, в частности, исследование устойчивости равновесия и устойчивости движения, а также механика тел переменной массы и теория удара. Общие законы динамики (закон об изменении количества движения, закон об изменении момента количества движения и закон об изменении кинетической энергии) являются базой для получения основных уравнений других наук, изучающих механическое движение упругих, жидких и газообразных тел.
Другую часть механики, непосредственно связанную с техникой, составляют многочисленные общетехнические и специальные дисциплины, такие, как гидравлика, сопротивление материалов, кинематика механизмов, динамика машин и механизмов, теория гироскопических устройств и приборов, внутренняя и внешняя баллистика, динамика ракет, теория движения различных наземных, морских и воздушных транспортных средств, строительная механика, ряд разделов технологии и др.
Некоторые из этих наук занимаются изучением механического движения тех же моделей реальных тел, что и вышеперечисленные науки (гидродинамика, теория упругости и др.), но подход к изучению этого движения у них другой, более близкий к инженерной практике. Так, например, гидравлика как и гидромеханика, занимается изучением механического движения жидких сред. Но, в отличие от гидромеханики, гидравлика характеризуется упрощенным подходом к изучению явлений течения жидкостей. В ней изучаются приближенные законы равновесия и движения жидкостей, и разрабатываются способы практического применения этих законов к расчетам искусственных и естественных русел, сооружений и машин. В большинстве случаев в гидравлике рассматриваются одномерные движения жидкостей.
Теория упругости и сопротивление материалов также занимаются изучением механического движения одной и той же модели – упругого тела. Однако подход к изучению механики упругих тел у них разный. Сопротивление материалов не занимается упругими свойствами анизотропных и неоднородных тел (например, кристаллов); предметом его изучения являются изотропные и однородные тела. Точность описания механики упругих сред у них тоже различна, так как в сопротивлении материалов применяются упрощающие гипотезы (такие, как гипотеза плоских сечений), позволяющие получить более простые, хотя и менее точные расчетные формулы. И, наконец, если теория упругости занимается только изучением напряженного состояния тел, то в курсе сопротивления материалов в первую очередь рассматривают вопросы прочности, вопросы подбора необходимых конструктивных элементов, способных выдержать заданные нагрузки.
Все перечисленные общетехнические и специальные дисциплины, а также ранее упоминавшиеся науки, изучающие механическое движение твердых, жидких и газообразных тел (гидромеханика, аэродинамика, газовая динамика, теория упругости, теория пластичности, реология), пользуются уравнениями и методами теоретической механики.
Раздел 1. К И Н Е М А Т И К А
Тема 1. «Кинематика точки»
§1. Основные понятия.
Теоретическая механика изучает движение в пространстве и времени.
Определение. Кинематикой называется раздел теоретической механики, в котором изучается механическое движение тел без учета физических причин, вызывающих это движение.
Определение. Под механическим движением в кинематике мы будем понимать изменение с течением времени пространственного взаимного расположения тел.
Характер движения одного и того же объекта будет разным в зависимости от того, по отношению к каким другим телам это движение будет рассматриваться. Например, известно, что траекториями планет относительно далеких звезд являются эллипсы, в то же время наблюдатель, находящийся на Земле, видит движение планет происходящим по сложным пространственным кривым. Для летчика, находящегося в кабине самолёта, движение ротора двигателя будет вращением вокруг неподвижной оси независимо от того, как двигался самолёт. Если при этом самолёт двигался поступательно и прямолинейно, то для наблюдателя, находящегося на Земле, движение ротора будет винтовым.
Т. о., при изучении движения тела, следует, прежде всего указать, по отношению к какой системе отсчета изучается движение. Систем отсчета существует достаточно много, мы будем работать в декартовой системе координат, снабженной часами.
Всё многообразие окружающих нас материальных объектов теоретическая механика объединила в три основные модели: материальная точка, система материальных точек, абсолютно твёрдое тело.
Определение. Материальной точкой называют простейшую модель материального тела любой формы, размеры которого достаточно малы, и которое можно принять за геометрическую точку (по сравнению с характерными размерами задачи), обладающую массой.
Определение. Системой материальных точек или механической системой называется любая совокупность материальных точек.
Определение. Абсолютно твёрдыми телами называют механическую систему, расстояния между точками которой не изменяются в процессе движения при любых взаимодействиях.
Все тела в природе в той или иной форме деформируемы, но в некоторых задачах этими деформациями можно пренебречь.
§ 2. Способы задания и уравнения движения точки. Траектория движения.
Движение точки считают заданным, если известно её положение в пространстве в любой момент времени. Существуют три способа задания движения: векторный, координатный и естественный.
1. Положение точки определено, если задан её радиус – вектор  , проведенный из неподвижной точки пространства.
, проведенный из неподвижной точки пространства.
Определение. Функциональная зависимость радиуса – вектора исследуемой точки от времени называется уравнением движения точки в векторной форме:
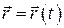 (1.1)
(1.1)
2. Положение точки в пространстве можно определить не только при помощи вектора  , но также при помощи скалярных величин–координат точки, заданных как функции времени. В частности, в декартовой прямоугольной системе координат уравнения движения точки можно написать с помощью трёх функций:
, но также при помощи скалярных величин–координат точки, заданных как функции времени. В частности, в декартовой прямоугольной системе координат уравнения движения точки можно написать с помощью трёх функций:
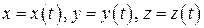 . (1.2)
. (1.2)
Понятно, что оба эти способа задания движения точки эквивалентны, т. к.
 . (1.3)
. (1.3)
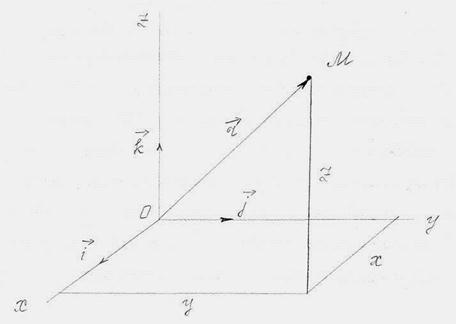
Рис. 1
!!!  Декартовы координаты не являются единственными координатами, применяемыми при описании движения точки.
Декартовы координаты не являются единственными координатами, применяемыми при описании движения точки.
В общем случае в качестве координат точки могут быть приняты значения любых трех функций декартовых координат
q 1=q1(x, y, z); q2 = q2(x, y, z); q3 = q3(x, y, z), (1.25)
ели только этими уравнениями х, у, z определяются как функции q 1, q2, q3, т.е.
x = x (q1, q2, q3); у = у (q1, q2, q3); z = z (q1, q2, q3). (1.25)
Таким образом, ни одно из уравнений (1.25) не должно противоречить другим и не должно являться следствием других.
Через каждую точку пространства в этом случае проходят три координатные поверхности, уравнения которых можно получить из выражений (1.25), положив криволинейные координаты равными тем иx значениям, которые определяют положение точки в фиксированный момент времени (т. е. некоторым фиксированным значениям):
q 1(x, y, z) = С1 ;
q2(x, y, z) = C2; (1.27)
q3 (х, у, z) = C3.
Имеем, таким образом, при различных значениях постоянных С1, С2, С3 три семейства координатных поверхностей. Если взять любую пару равенств (1.27), например
q2(x, y, z) = C2;
q3 (х, у, z) = C3. (1.28)
то равенства (1.28) представляют собой уравнения координатной линии. Вдоль этой линии меняется только одна координата q1. Очевидно, что через каждую точку пространства проходят три координатные линии (см. рис. 11).
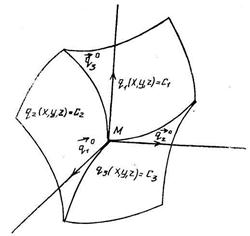
Рис.11
Положительными направлениями координатных линий считаются те, которым отвечают возрастающие значения соответствующих координат. Так как координатные линии являются кривыми линиями, то рассматриваемая система координат общего вида называется криволинейной.
Если подставить в правую часть соотношения (1.3) вместо, декартовых координат их значения, выраженные через криволинейные координаты q1, q2, q3 (1.26), то получим зависимость радиус-вектора от криволинейных координат:
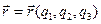 (1.29)
(1.29)
Если рассматривать теперь движущуюся точку, то определяющие ее криволинейные координаты будут меняться с течением времени, и уравнения движения точки в криволинейных координатах будут иметь вид:
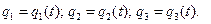 (1.30)
(1.30)
Рассмотрим произвольную вектор–функцию  скалярного аргумента a.
скалярного аргумента a.
Определение. Годографом вектор–функции  скалярного аргумента a называется геометрическое место концов вектор–функции
скалярного аргумента a называется геометрическое место концов вектор–функции  , полученных при всех возможных значениях аргумента a, если начало вектор–функции
, полученных при всех возможных значениях аргумента a, если начало вектор–функции  откладывать от фиксированной точки, называемой полюсом годографа.
откладывать от фиксированной точки, называемой полюсом годографа.
Годограф представляет собой некоторую кривую линию. Ту сторону годографа, в направлении которой движется конец вектора при возрастании переменной a, называют стороной возрастания аргумента, противоположную сторону – стороной убывания аргумента.
Если скалярному аргументу a сообщить некоторые приращения Da, то вектор  получит приращение
получит приращение
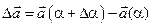 . (1.31)
. (1.31)
 Рис. 12
Рис. 12
| Вектор  направлен по хорде годографа в положительную сторону, если Da >0, и в отрицательную сторону, если Da <0.
Производная вектор–функции направлен по хорде годографа в положительную сторону, если Da >0, и в отрицательную сторону, если Da <0.
Производная вектор–функции  по скалярному аргументу a представляет собой предел по скалярному аргументу a представляет собой предел
 (1.32)
при стремлении приращения аргумента Da к нулю. (1.32)
при стремлении приращения аргумента Da к нулю.
|
Так как вектор  направлен по хорде в положительную сторону при Da >0 и в отрицательную сторону при Da <0, то в обоих случаях отношение
направлен по хорде в положительную сторону при Da >0 и в отрицательную сторону при Da <0, то в обоих случаях отношение  направлено по хорде в положительную сторону.
направлено по хорде в положительную сторону.
Перейдя к пределу при Da® 0, получим утверждение: производная вектор–функции  по скалярному аргументу a направлена по касательной к годографу вектор–функции
по скалярному аргументу a направлена по касательной к годографу вектор–функции  всторону возрастания аргумента.
всторону возрастания аргумента.
В общем случае годограф вектор–функции  есть пространственная кривая, вид которой зависит от закона изменения вектора функции. Так, например, годографом постоянной вектор–функции является точка (рис.13, а), годографом вектор–функции сохраняющей направление, является прямая, имеющая направление вектор–функции и проходящая через полюс годограф (рис.13,б), годографом вектора–функции, сохраняющей величину, является кривая, лежащая не сфере, центр которой находится в полюсе годографа и радиус которой равен величине вектор–функции (рис.13, в). Учитывая теперь, что производная от вектор–функции направлена по касательной к годографу, и что она является скоростью точки годографа, придем к следующим выводам.
есть пространственная кривая, вид которой зависит от закона изменения вектора функции. Так, например, годографом постоянной вектор–функции является точка (рис.13, а), годографом вектор–функции сохраняющей направление, является прямая, имеющая направление вектор–функции и проходящая через полюс годограф (рис.13,б), годографом вектора–функции, сохраняющей величину, является кривая, лежащая не сфере, центр которой находится в полюсе годографа и радиус которой равен величине вектор–функции (рис.13, в). Учитывая теперь, что производная от вектор–функции направлена по касательной к годографу, и что она является скоростью точки годографа, придем к следующим выводам.
 Рис. 13
Рис. 13
| В случае рис. 13,а скорость точки годографа равна нулю, так как точка не перемещается. Отсюда очевидный вывод: производная постоянной вектор–функции равна нулю. В случае рис.13,б годограф – прямая, поэтому скорость точки годографа направлена по этой прямой. Отсюда следует, что производная вектор–функции, сохраняющей направление, коллинеарна вектор–функ-ции (рис.13,б). В случае рис.13,в скорость точки годографа лежит в касательной плоскости к сфере, на которой расположен годограф. Поэтому скорость точки годографа будет перпендикулярна радиус–вектору 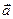 , описывающему годограф (рис.13,в). Следовательно, производная от вектор–функции, сохраняющей величину, перпендикулярна вектор–функции. , описывающему годограф (рис.13,в). Следовательно, производная от вектор–функции, сохраняющей величину, перпендикулярна вектор–функции.
|
Заметим также, что в общем случае модуль производной от вектор –функции по некоторому скалярному аргументу не равен производной от модуля этой функции по указанному аргументу, т. е.
 .
.
В самом деле, при вычислении величины, стоящей слева, учитывается изменение величины и направления вектора 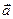 , в то время как величина, стоящая справа, изменение направления вектора отвечающее изменению аргумента a, не учитывает. Поэтому равенство
, в то время как величина, стоящая справа, изменение направления вектора отвечающее изменению аргумента a, не учитывает. Поэтому равенство
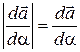
имеет место только для специальных вектор–функций скалярного аргумента, а именно тех, направление которых не меняется с изменением аргумента, т. е. вектор–функций вида
 ,
,
где 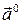 – постоянный вектор.
– постоянный вектор.
Применяя теперь приведенные выше соображения к изучению зависимостей вектора  от каждой из криволинейных координат q1, q2, q3, придем к выводу, что производные от вектора
от каждой из криволинейных координат q1, q2, q3, придем к выводу, что производные от вектора 
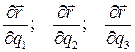 (1.33)
(1.33)
полученные при изменении только одной из трех криволинейных координат (они называются частными производными), направлены по 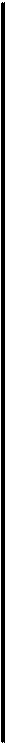 касательным к соответствующим координатным линиям в сторону возрастания координат.
касательным к соответствующим координатным линиям в сторону возрастания координат.
С помощью векторов (1.33) можно образовать тройку ортов криволинейной системы координат
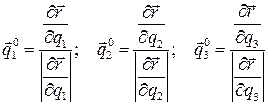 . (1.34)
. (1.34)
Если орты (1.34) взаимно ортогональные, то криволинейная система координат называется ортогональной.
Для ортогональной системы криволинейных координат
 , (1.35)
, (1.35)
где 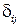 – символ Кронекера, который определяется следующими условиями:
– символ Кронекера, который определяется следующими условиями:

Рассмотрим некоторые системы ортогональных криволинейных координат, применяемые в теоретической механике.
Цилиндрические координаты. Формулы перехода от декартовых координат х, у, z к цилиндрическим координатам r, j, z имеют вид:
x = rcosj; y = rsinj; z = z. (1.36)
Обратный переход производится по формулам:
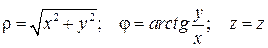 . (1.37)
. (1.37)
Координатные поверхности описываются уравнениями
 . (1.38)
. (1.38)
Из уравнений (1.38) видно, что одна из этих поверхностей есть прямой круговой цилиндр, причем ось Oz является его осью симметрии, другая поверхность есть плоскость, проведенная через ось Oz, третья поверхность есть плоскость, перпендикулярная этой оси. Координатные поверхности, а также орты криволинейных цилиндрических координат изображены на рисунке.

Рис. 14
Из равенства (1.3) и (1.36) имеем
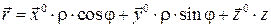 , (1.39)
, (1.39)
откуда
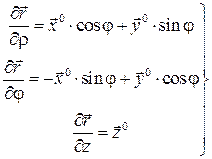 . (1.40)
. (1.40)
Из (1.40) получаем
 . (1.41)
. (1.41)
Пользуясь соотношениями (1.34), (1.40), (1.41) найдем орт цилиндрической системы координат:
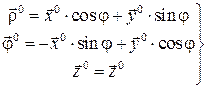 . (1.42)
. (1.42)
Уравнения движения точки в цилиндрических координатах имеют вид
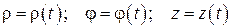 . (1.43)
. (1.43)
Сферические координаты. Формулы перехода от декартовых координат х, у, z к цилиндрическим координатам r, q, j имеют вид:
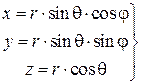 . (1.44)
. (1.44)
Обратный переход производится по формулам:
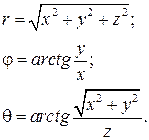 (1.45)
(1.45)
Координатные поверхности описываются уравнениями
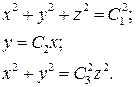 (1.46)
(1.46)
Из уравнений (1.46) видно, что одна из этих поверхностей есть сфера с центром в начале координат; вторая поверхность есть плоскость, проведенная через ось Oz; третья поверхность есть круговой конус, имеющий в качестве оси симметрии ось Оz (см. рис.15).
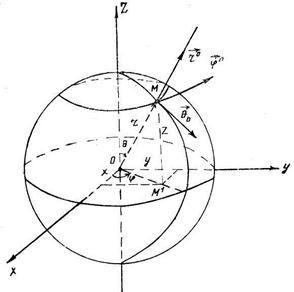
Рис. 15
Из равенства (1.3) и зависимостей (1.23) получим
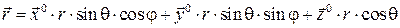 , (1.47)
, (1.47)
откуда
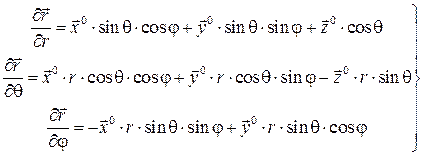 . (1.48)
. (1.48)
Из (1.48) получаем 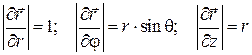 . (1.49)
. (1.49)
Пользуясь соотношениями (1.34), (1.48), (1.49) найдем орт сферической системы координат:
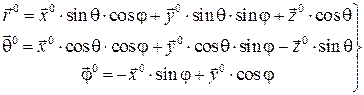 . (1.50)
. (1.50)
!!! Уравнения движения точки в сферических координатах имеют вид
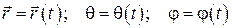 . (1.51)
. (1.51)
Определение. Геометрическое место последовательно занимаемых точкой положений в заданной системе отсчета называется траекторией точки.
Траектория движущейся точки может быть прямолинейной или криволинейной. Вид траектории зависит от выбранной системы отсчета. Например, при бомбометании траектория падения бомбы относительно самолёта – это прямая линия, а относительно Земли – парабола.
Уравнения движения в форме (1.1) и (1.2) являются одновременно и уравнениями траектории в параметрическом виде, не дающем наглядного представления о виде траектории. Для устранения этой проблемы нужно перейти от уравнений в параметрическом виде к уравнениям в координатной форме, исключая параметр t – время.
Например,
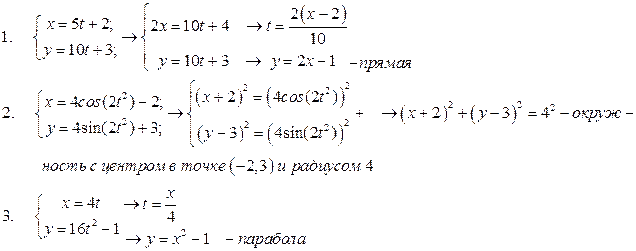
3. Часто необходимо определить положение точки при её движении по наперёд заданной траектории. Уравнения кривой по которой движется точка при помощи декартовых координат записываются в виде: 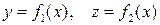 . Этих уравнений недостаточно для определения положения точки в пространстве в любой момент времени. Зададим закон движения по траектории с помощью длины дуги, которую будем называть дуговой координатой s = s(t).
. Этих уравнений недостаточно для определения положения точки в пространстве в любой момент времени. Зададим закон движения по траектории с помощью длины дуги, которую будем называть дуговой координатой s = s(t).
Выберем некоторую фиксированную точку, от которой будем отсчитывать s, и положительное направление отсчета. Тогда положение точки М в пространстве будет определено однозначно.

Рис. 2
Итак, задание движения точки при помощи задания уравнений траектории и длины дуги как функции времени называют естественным способом задания движения.
 (1.4)
(1.4)
§ 3. Путь, пройденный точкой.
Изменение дуговой координаты  за время
за время 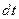 может быть как положительным, так и отрицательным. Введём функцию S, дифференциал которой равен
может быть как положительным, так и отрицательным. Введём функцию S, дифференциал которой равен 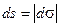 .
.
В свою очередь 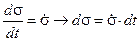 . Тогда
. Тогда  .
.
Определение. Путь, пройденный точкой за промежуток времени 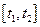 – это интеграл вида
– это интеграл вида
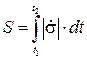 .
.
Необходимо помнить, что отождествлять координату s(t) с длиной пути S нельзя.

Рис. 3
Рассмотрим прямолинейное движение точки. Пусть в начальный момент времени 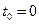 точка занимала положение М0. За промежуток времени
точка занимала положение М0. За промежуток времени  она дважды проходит отрезок М0 М длиной а (“ туда и обратно ”). При этом s (t0)=ОМ0, при s (t – t0)=ОМ0, т.е.дуговая координата не изменилась, а путь пройденный за это же время S= 2а.
она дважды проходит отрезок М0 М длиной а (“ туда и обратно ”). При этом s (t0)=ОМ0, при s (t – t0)=ОМ0, т.е.дуговая координата не изменилась, а путь пройденный за это же время S= 2а.
§ 4. Скорость точки.
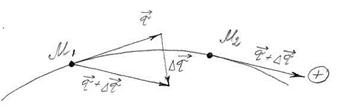
Пусть М1 и М2 – положения движущейся точки в момент времени t и 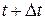 . Вектор
. Вектор 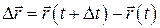 , соединяющий начальное и конечное положение точки называется перемещением точки за промежуток времени
, соединяющий начальное и конечное положение точки называется перемещением точки за промежуток времени 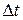 .
.
 Определение. Средней скоростью за промежуток времени
Определение. Средней скоростью за промежуток времени 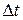 называется отношение вектора перемещения ко времени, за которое оно произошло:
называется отношение вектора перемещения ко времени, за которое оно произошло:
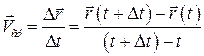 . (1.5)
. (1.5)
Направление 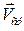 совпадает с направле-нием перемещения. Чем меньше промежуток времени
совпадает с направле-нием перемещения. Чем меньше промежуток времени 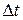 , тем более точно представит средняя скорость быстроту перемещения. Естественно при этом перейти к пределу.
, тем более точно представит средняя скорость быстроту перемещения. Естественно при этом перейти к пределу.
|
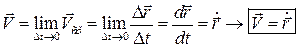 . (1.6)
. (1.6)
Определение. Скоростью точки называют производную её радиус–вектора по времени.
Поскольку предельное положение хорды М1М2 при стремлении М2 к М1 есть касательная к траектории в данной точке, то и скорость в любой момент времени направлена по касательной к траектории в сторону движения точки.
Из определения скорости вытекает, что её размерность равна

 .
.
Продифференцируем по времени выражение (1.3), получим:
 . (1.7)
. (1.7)
С другой стороны, скорость точки, как и любой вектор, может быть представлена через свои проекции на координатные оси:
 . (1.8)
. (1.8)
Сравнивая выражения (1.7) и (1.8), получим: 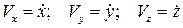 .
.
Величина скорости равна
 . (1.9)
. (1.9)
Направление скорости определяется косинусами углов, составляемых вектором скорости с осями координат:
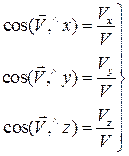 (1.10)
(1.10)
Перейдём к вычислению скорости точки при естественном способе задания её движения. Считая, что зависимости 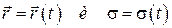 заданы, найдём:
заданы, найдём:
 . (1.11)
. (1.11)
Если мы вспомним, что предел отношения длины хорды к соответствующей ей дуге кривой при стремлении дуги к нулю равен единице, то 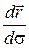 определяет единичный вектор касательной
определяет единичный вектор касательной  .
.
Т. к. 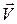 коллинеарен касательной к траектории, то
коллинеарен касательной к траектории, то 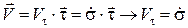 .
.
§ 5. Сопровождающий трёхгранник, кривизна, радиус кривизны кривой в заданной точке.
С каждой точкой М пространственной кривой мы можем связать три взаимно перпендикулярных прямые и три плоскости, взаимно пересекающиеся под прямыми углами в точке М. Укажем на чертеже эти прямые и плоскости:
| прямые | – касательная с единичным вектором  , направленная в положительную сторону движения;
– главная нормаль с единичным вектором , направленная в положительную сторону движения;
– главная нормаль с единичным вектором  , направленная всегда в сторону вогнутости кривой;
– бинормаль с единичным вектором , направленная всегда в сторону вогнутости кривой;
– бинормаль с единичным вектором  , направленная так, чтобы вектора , направленная так, чтобы вектора  , , и и 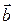 образовывали правую тройку; образовывали правую тройку;
|
| плоскости | – соприкасающаяся плоскость содержит в себе касательную и главную нормаль. Среди всех плоскостей, проходящих через точку М, эта плоскость наиболее тесно прилегает к кривой; – нормальная плоскость содержит в себе главную и бинормаль; – спрямляющая плоскость содержит касательную и бинормаль. |
Образованный этими плоскостями трёхгранник называется естественным или трёхгранником Фрэнэ, а перечисленные прямые – естественными или сопровождающими осями, т. к. при движении точки по кривой естественный трёхгранник движется вместе с точкой как твердое тело, поворачиваясь вокруг вершины, совпадающей с движущейся точкой.
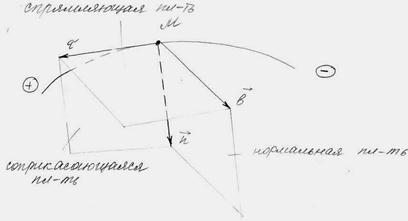
Рис. 5
Кривизна кривой в точке М – число, характеризующее отклонение кривой в окрестности точки М от прямой.
 Рис. 6
Рис. 6
| Проведём в точке М кривой касательную  .В другой близкой точке кривой М1, отстоящей от М на расстоянии .В другой близкой точке кривой М1, отстоящей от М на расстоянии 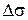 , построим касательную , построим касательную 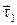 .
Проведём в точке М прямую .
Проведём в точке М прямую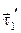 параллельную параллельную 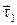 . Угол . Угол 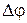 между линиями между линиями  и и 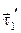 называют углом смежности. называют углом смежности.
|
Определение. Кривизной кривой К в точке М называют предел, к которому стремится угол смежности, приходящийся на единицу расстояния 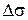 , при стремлении
, при стремлении 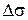 к нулю, т.е.
к нулю, т.е.
 .
.
Определение. Радиусом кривизны кривой 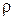 в точке М называют величину, обратную кривизне кривой в этой точке, т.е.
в точке М называют величину, обратную кривизне кривой в этой точке, т.е.
 .
.
Пример. Вычислим радиус кривизны дуги окружности радиуса R.
 Рис. 7
Рис. 7
| Дуга окружности длиной s, опирающаяся на центральный угол j, выражается зависимостью s = Rj.
Для радиуса кривизны имеем:
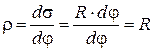 , т. е. для окружности радиус кривизны в каждой её точке один и тот же и совпадает с радиусом окружности. ■ , т. е. для окружности радиус кривизны в каждой её точке один и тот же и совпадает с радиусом окружности. ■
|
§ 6. Ускорение точки.
Определение. Ускорением точки 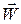 называется производная от её скорости по времени, или вторая производная от её радиуса – вектора по времени.
называется производная от её скорости по времени, или вторая производная от её радиуса – вектора по времени.
 (1.12)
(1.12)
Из определения ускорения вытекает, что его размерность равна
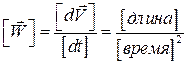 .
.
Для определения ускорения в декартовой системе отсчёта, продифференцируем по времени выражения (1.7) и (1.8).
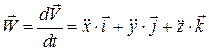 , (1.13)
, (1.13)
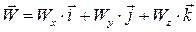 . (1.14)
. (1.14)
Сравнивая (1.13) и (1.14), получим:
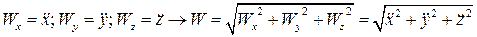 . (1.15)
. (1.15)
Направление ускорения по отношению к декартовым осям устанавливается по соотношениям:
 (1.16)
(1.16)
Продифференцируем соотношение (1.11):
 . (1.18)
. (1.18)
Из постоянства величины вектора  следует, что вектор
следует, что вектор 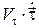 перпендикулярен вектору
перпендикулярен вектору  . При произвольном пространственном движении точки сказанного мало для определения направления этого слагаемого.
. При произвольном пространственном движении точки сказанного мало для определения направления этого слагаемого.
Рассмотрим сначала движение точки по плоской кривой.
Вычислим 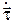 . Величина вектора
. Величина вектора 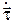 равна
равна 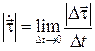 .
.
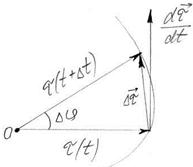 Рис. 8 Рис. 8
| 
|
Из чертежа видно, что  . Тогда
. Тогда
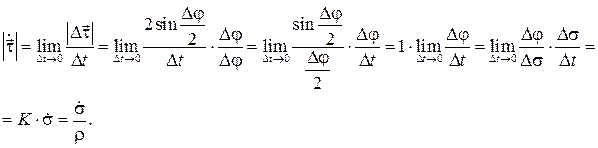 Направлен вектор
Направлен вектор 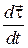 перпендикулярно к самому вектору
перпендикулярно к самому вектору  . Для доказательства этого используем тождество
. Для доказательства этого используем тождество 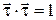 . Дифференцируем по времени обе части этого тождества, получим
. Дифференцируем по времени обе части этого тождества, получим 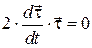 . Каждый из сомножителей этого выражения не равен нулю, поэтому
. Каждый из сомножителей этого выражения не равен нулю, поэтому  , т.е.
, т.е. 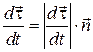 .
.
Окончательно будем иметь:
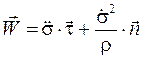 . (1.19)
. (1.19)
Можно показать, что при смещении из точки М по кривой, уклонение точки от соприкасающейся плоскости будет бесконечно малым, не ниже 3–го порядка малости относительно приращения дуги. Поэтому всякую пространственную кривую в малой окрестности каждой точки можно считать приближенно плоской и расположенной в соприкасающейся плоскости.
С другой стороны, ускорение точки может быть представлено через проекции на оси естественного трёхгранника:
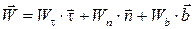 . (1.20)
. (1.20)
Сравнивая выражения (1.19) и (1.20), получим:
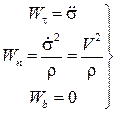 (1.21)
(1.21)
Учитывая ортогональность 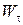 и
и 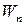 , получим:
, получим:
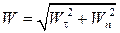 . (1.22)
. (1.22)
Зная 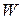 и
и 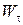 , можно найти
, можно найти 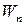 :
: 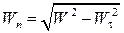 . (1.23)
. (1.23)
Тогда  . (1.24)
. (1.24)
Проанализируем зависимости (1.21). Из того, что 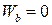 следует, что полное ускорение точки расположено в соприкасающейся плоскости траектории.
следует, что полное ускорение точки расположено в соприкасающейся плоскости траектории.
Случаи обращения в нуль касательного ускорения получают из условия
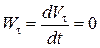 .
.
Это условие выполняется всё время, пока  , т.е. при равномерном движении точки по траектории любой формы. Либо в те моменты времени, в которые скорость
, т.е. при равномерном движении точки по траектории любой формы. Либо в те моменты времени, в которые скорость 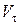 достигает экстремума (минимума – максимума).
достигает экстремума (минимума – максимума).
 Рис. 9
Рис. 9
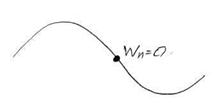 Рис. 10
Рис. 10
| При колебаниях маятника эти моменты соответствуют его прохождению через точку А.
Случаи обращения в нуль нормального ускорения следуют из условия 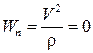 .
Нормальное ускорение обращается также в нуль в моменты времени, в которые .
Нормальное ускорение обращается также в нуль в моменты времени, в которые  , т.е. в моменты изменения направления движения точки по траектории. Для маятника такими моментами являются моменты отклонения маятника на наибольший угол как в одну так и в другую сторону. Эти моменты соответствуют мгновенным остановкам маятника.
Это условие выполняется при , т.е. в моменты изменения направления движения точки по траектории. Для маятника такими моментами являются моменты отклонения маятника на наибольший угол как в одну так и в другую сторону. Эти моменты соответствуют мгновенным остановкам маятника.
Это условие выполняется при 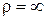 , т.е. при прямолинейном движении или в точках перегиба траектории, в которых происходит изменение выпуклости траектории на вогнутость, и наоборот. , т.е. при прямолинейном движении или в точках перегиба траектории, в которых происходит изменение выпуклости траектории на вогнутость, и наоборот.
|
Случаи обращения в нуль касательного (тангенциального) и нормального ускорений, а также общие формулы для них показывают, что касательное ускорение характеризует изменение скорости по величине, а нормальное – по направлению.
§ 7. Частные случаи движения точки.
Равномерное движение.
Определение. Равномерным называется такое движение, при котором величина скорости остаётся постоянной  .
.
Т. к.  , то
, то 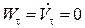 , т.е. полное ускорение равно нормальному. Определим путь, пройденный точкой при равномерном движении.
, т.е. полное ускорение равно нормальному. Определим путь, пройденный точкой при равномерном движении.
 .
.
Равнопеременное движение.
Определение. Равнопеременным движением называют такое движение по траектории любой формы, при котором касательное ускорение 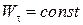 .
.
Если при движении точки модуль скорости увеличивается, то движение называется ускоренным, если уменьшается – замедленным.
Условие ускоренного движения:  (т.е. скорость и ускорение направлены в одну и ту же сторону).
(т.е. скорость и ускорение направлены в одну и ту же сторону).
Условие замедленного движения: 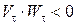 (т.е. скорость и ускорение направлены в противоположные стороны).
(т.е. скорость и ускорение направлены в противоположные стороны).
Определим скорость точки в некоторый момент времени и путь, пройденный точкой за некоторый промежуток времени.
Пусть при  . Тогда
. Тогда
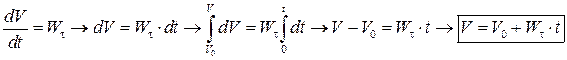 .
.
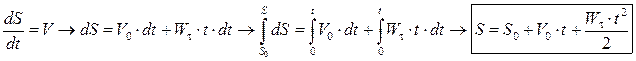 .
.
|
|
Дата добавления: 2014-01-20; Просмотров: 783; Нарушение авторских прав?; Мы поможем в написании вашей работы!