Тема 2. “ Простейшие движения твёрдого тела”

Лекция № 4

Знать движение тела – это означает знать его положение в пространстве в любой момент времени. Положение твёрдого тела в пространстве определяется положением трёх его точек, которые не лежат на одной прямой. Положение каждой точки в пространстве задаётся тремя скалярными параметрами – координатами. Следовательно, положение тела можно задать девятью параметрами. Однако, согласно определению абсолютно твёрдого тела, расстояния между его точками не меняются в процессе движения, т.е.

Рис. 16

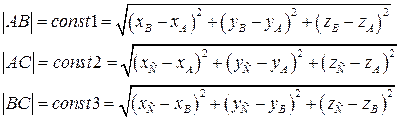Таким образом, независимых координат, определяющих положение тела, будет 9–3=6. Определение. Числом степеней свободы твёрдого тела называют число независимых параметров, однозначно определяющих положение тела относительно рассматриваемой системы отсчета.

Твёрдое тело, которое может без помех и ограничений двигаться в любом направлении, называется свободным. Свободное твёрдое тело имеет 6 степеней свободы. Когда существуют ограничения движению, тело будет иметь меньше степеней свободы.

Имеется два простейших вида движения твердого тела, комбинированием которых можно получать другие, более сложные его движения. Такими движениями являются поступательное движение и вращение вокруг неподвижной оси.

§ 1. Поступательное движение твёрдого тела.

Определение. Поступательным называется такое движение твердого тела, при котором любая прямая, жестко скреплённая с телом, остаётся параллельной своему первоначальному положению в каждый момент времени.

Поступательно движутся педали у велосипеда относительно его рамы, поршни в цилиндрах двигателя внутреннего сгорания относительно цилиндров, кабины колеса обозрения относительно Земли в парках.

Траектории точек у поступательно движущегося твёрдого тела могут быть не только прямыми, но и любыми кривыми, в том числе и окружностями. Например, все точки спарника, который соединяет пальцы равных кривошипов, описывают в процессе движения окружности.

Свойства поступательного движения характеризует следующая теорема.

Теорема: При поступательном движении твердого тела траектории, скорости и ускорения всех точек тела одинаковы.

Доказательство: Выберем в теле две произвольные точки А и В. Положения этих точек зададим их радиус–векторами, которые связаны между собой условием: 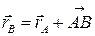. (2.1)

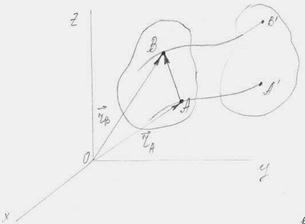Рис. 17

Для любого твердого тела вектор 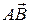является постоянным по величине, а при поступательном движении он не изменяется и по направлению. Траектория точки В может быть получена параллельным переносом траектории точки А. Продифференцируем по времени соотношение (2.1): .

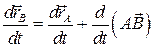Т. к. 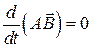, то 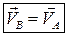. (2.2)

Продифференцировав (2.2), получим . (2.3)

■

Мы видим, что поступательное движение характеризуется движением одной точки тела. Для задания этого движения достаточно задать координаты этой точки тела как функции времени, т.е.

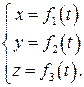(2.4)

Следовательно, твёрдое тело, совершающее поступательное движение, имеет три степени свободы и уравнения (2.4) являются уравнениями поступательного движения твёрдого тела.

§ 2. Вращение твёрдого тела вокруг неподвижной оси.

Определение. Вращением твёрдого тела вокруг неподвижной оси называется такое движение, при котором в теле существует неподвижная прямая, которая называется осью вращения.

Если выбрать две точки на оси вращения (А и В), которую для удобства выберем совпадающей с осью z, то движение тела определится движением одной его точки – точки С.

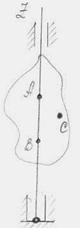Рис. 18 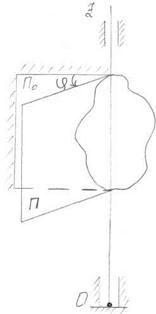  Рис. 19

Из трёх параметров, определяющих движение точки С, независимым будет только один, потому что два других связаны зависимостями: Т. о., для определения движения тела при вращении вокруг неподвижной оси, достаточно задать один параметр. Выберем этот параметр. Через ось вращения проведём две плоскости: одну неподвижную П0, а другую П, жестко связанную с твёрдым телом и вращающуюся вместе с ним. Двугранный угол j между этими полуплоскостями, который отсчитывается от неподвижной плоскости П0, называется углом поворота тела. Положительное направление отсчета угла j выбирается так, чтобы со стороны положительного направления оси z увеличение угла происходило против движения стрелки часов. Уравнение 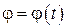(2.5) называется уравнением вращения твёрдого тела вокруг неподвижной оси. При вращении твёрдого тела вокруг неподвижной оси все его точки будут описывать окружности, которые размещаются в плоскостях, перпендикулярных оси вращения, а центры их лежат на этой оси.

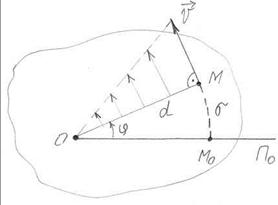Рассмотрим точку М, расположен-ную на расстоянии d от оси вращения. Выберем начало отсчета дуговой коор-динаты в точке М₀ – точке пересечения траектории с неподвижной плоскостью П₀. Вычислим дуговую координату s точки М.

. (2.6)

Рис. 20

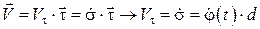Вычислим скорость точек тела. Движение точек задано естественным способом, поэтому . Поскольку ,

то .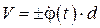

Определение. Угловой скоростью тела называется вектор, направленный вдоль оси вращения тела в ту сторону, откуда вращение тела видно против движения стрелки часов и проекция которого на ось вращения равна первой производной от угла поворота по времени:

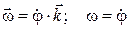. (2.7)

Размерность w [1/с] или [рад/с].

Тогда 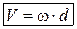. (2.8)

Скорости точек тела при вращении вокруг неподвижной оси пропорциональны их кратчайшим расстояниям до этой оси. Коэффициентом пропорциональности является угловая скорость. Скорости точек направлены по касательным к траекториям и, следовательно, перпендикулярны радиусам вращения.

Определим скорость любой точки тела через вектор угловой скорости.

Теорема: Скорость любой точки тела при его вращении вокруг неподвижной оси равна векторному произведению угловой скорости тела на радиус–вектор точки, проведенный из любой точки на оси вращения:

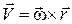. (2.9)

Доказательство:

Покажем, что векторы и имеют равные величины и одинаково направлены.

1. Величина вектор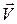а равна 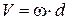согласно (2.8). Величина векторного произведения: 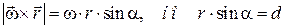. Тогда 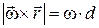. Т. о., величины векторов одинаковы.

2. Направления этих векторов тоже совпадают.

Рис. 21

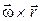Скорость точки М направлена по касательной к окружности радиуса d в сторону вращения тела, т.е. она перпендикулярна плоскости, проведенной через ось и точку. С другой стороны, по правилам векторного произведения, вектор тоже перпен-дикулярен к этой же плоскости направлен а ту же сторону.

■

Определим ускорение точки. По определению 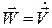, поэтому

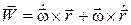. (2.10)

Обозначим и назовём угловым ускорением.

Определение. Угловое ускорение тела направлено вдоль оси вращения, и его проекция на ось вращения равна второй производной от угла поворота по времени.

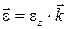. (2.11)

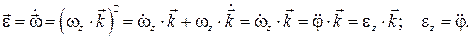
Т. к. 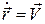, то . (2.12)

Обозначим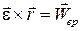

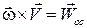
– вращательное ускорение;   – осестремительное ускорение.

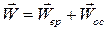. (2.13)

Рис. 22

Из определения вращательного ускорения следует, что его величина 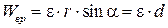(2.14) Направление вращательного ускорения (по правилам векторного произведения) коллинеарно скорости точки. Из определения осестремительного ускорения следует: 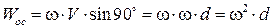(2.15) Направлено осестремительное ускорение по радиусу окружности к оси вращения.

Т. к. 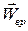и 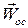перпендикулярны, то величина полного ускорения точки равна 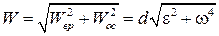. (2.16)

Частные случаи вращения тела.

Равномерное вращение.

Определение. Равномерным называется такое вращение тела вокруг неподвижной оси, при котором .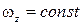

Т. к. 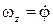, то .

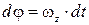После интегрирования получим 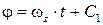, где С₁ – угол поворота j при t = 0, т.е. j_{0 .} Тогда 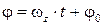. В этом выражении 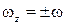, но поскольку при равномерном вращении тело не может изменить направление вращения, то .

Окончательно 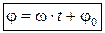. (2.17)

Равнопеременное вращение.

Определение. Равнопеременным называется такое вращение тела, при котором .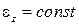

Пусть при 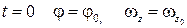. Тогда . После интегрирования 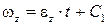. Из начальных условий при .

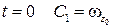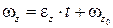. (2.18)

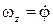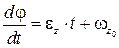Т. к. , то После интегрирования получим

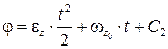. Из начальных условий .

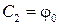Таким образом, 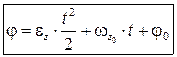. (2.19)

Вращение будет ускоренным, если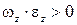, и замедленным, если 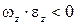. Это следует из того, что .

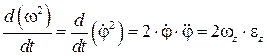§ 3. Теорема о сложении скоростей.

Иногда при решении задач механики целесообразно рассматривать движение точки то отношению к нескольким системам отсчета одновременно. Одна из этих систем при этом условно считается неподвижной, а другая определенным образом движется по отношению к первой.

Определение. Движение, происходящее по отношению к двум системам отсчета, одна из которых при этом считается неподвижной, а другая определенным образом движется по отношению к первой, называется сложным.

Например, движение космического корабля, движущегося к Луне, нужно рассматривать одновременно относительно Земли и относительно Луны, которая сама движется относительно Земли. Самолёт, движущийся по палубе авианосца (авианосец – подвижная система отсчета) совершает сложное движение относительно берега (с берегом связана неподвижная система). Сложным будет движение вибраторов антенн радиотелескопов систем обнаружения, связи и прицеливания.

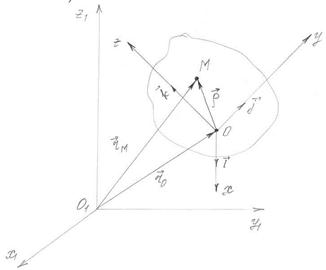Введём неподвижную систему отсчета 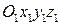. Относительно неё движется другая система – 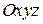. Движение точки будет восприни-маться наблюдателями, связанными с подвижной и неподвижной система-ми отсчета по-разному.

Рис. 23

Определение. Неподвижную систему отсчета называют абсолют-ной, подвижную систему – переносной или переносящей средой.

Определение. Движение точки относительно абсолютной системы называют абсолютным, относительно переносной системы – относительным.

Определение. Скорость и ускорение точки, вычисленные относительно абсолютной системы, называют абсолютной скоростью 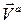и абсолютным ускорением .

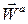Определение. Скорость и ускорение точки, вычисленные относительно переносящей среды, называют относительной скоростью 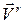и относительным ускорением точки .

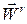Определение. Скорость и ускорение той точки переносящей среды, с которой в данный момент совпадает исследуемая точка, называют переносной скоростью 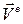и переносным ускорением .

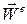Вычислим абсолютную скорость точки. По заданным уравнениям движения переносной системы и уравнениям относительного движения точки можно найти уравнения абсолютного движения. Зная их можно определить скорость относительно абсолютной системы отсчета. Но этот способ слишком громоздкий и сложный. Значительно удобнее по уравнениям относительного движения точки и уравнениям движения переносящей среды непосредственно определять скорость в абсолютной системе.

Теорема: Абсолютная скорость точки равна сумме переносной и относительной скоростей.

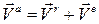. (2.20)

(Доказательство этой теоремы будет приведено далее.)

Дата добавления: 2014-01-20