Статистические методы контроля качества

Среди статистических методов контроля качества наиболее распространены так называемые семь инструментов контроля качества:

1) диаграмма Парето;

2) причинно-следственная диаграмма Исикавы;

3) контрольная карта;

4) гистограмма;

5) диаграмма разброса;

6) метод расслоения;

7) контрольные листки.

В своей совокупности эти методы образуют эффективную систему методов контроля и анализа качества. Семь простых методов могут применяться в любой последовательности, в любом сочетании, в различных аналитических ситуациях, их можно рассматривать и как целостную систему, и как отдельные инструменты анализа. В каждом конкретном случае предлагается определить состав и структуру рабочего набора методов. «Семь инструментов контроля качества» активно используются японскими фирмами.

1. Диаграмма Парето позволяет наглядно представить величину потерь в зависимости от различных объектов; представляет собой разновидность столбиковой диаграммы, применяемой для наглядного отображения рассматриваемых факторов в порядке уменьшения их значимости.

В 1897 г. итальянский экономист В. Парето предложил формулу, описывающую неравномерность распределения благ. Эта же идея в 1907 г. была графически проиллюстрирована на диаграмме американским экономистом М. Лоренцом. Оба ученых показали, что чаще всего наибольшая доля доходов или благ принадлежит небольшому числу людей. Известный американский специалист по управлению качеством Дж. Джуран применил этот подход в области контроля качества. Это дало возможность разделить факторы, влияющие на качество, на немногочисленные существенно важные и многочисленные несущественные. Оказалось, что, как правило, подавляющее число дефектов и связанных с ними потерь возникает из-за относительно небольшого числа причин. Дж. Джуран назвал этот подход анализом Парето.

Для построения диаграммы Парето исходные данные представляют в виде таблицы, в первой графе которой указывают анализируемые факторы, во второй — абсолютные данные, характеризующие число случаев обнаружения анализируемых факторов в рассматриваемый период, в третьей — суммарное число факторов по видам, в четвертой — их процентное соотношение, в пятой — кумулятивный (накопленный) процент случаев обнаружения факторов

.

Начинают построение диаграммы Парето с того, что на оси абсцисс откладывают данные графы 1, а на оси ординат — данные графы 2, располагаемые в порядке убывания частоты встречаемости. «Прочие факторы» всегда располагают на оси ординат последними; если доля этих факторов сравнительно велика, то необходимо сделать их расшифровку, выделив при этом наиболее значительные. По этим исходным данным строят столбиковую диаграмму, а затем, используя данные графы 5 и дополнительную ординату, обозначающую кумулятивный процент, вычерчивают кривую Лоренца. Возможно построение диаграммы Парето, когда на основной ординате откладывают данные графы 4; в этом случае для вычерчивания кривой Лоренца нет необходимости включать в диаграмму дополнительную ординату (именно этот вариант диаграммы наиболее распространен на практике).

Определяющим достоинством диаграммы Парето является то, что она дает возможность разделить факторы на значительные (встречающиеся наиболее часто) и на незначительные (встречающиеся относительно редко). Например, анализ диаграммы, представленной на рис. (а также кривой Лоренца), показывает, что усадочные раковины, газовая пористость и прочие трещины в литых деталях составляют 89,5% всех несоответствий. Следовательно, с устранения именно этих несоответствий следует начинать работу по обеспечению качества деталей.

Построение диаграммы Парето часто обнаруживает закономерность, получившую название «Правило 80/20» и основанную на принципе Парето, согласно которому большая часть следствий вызывается относительно немногочисленными причинами. Применительно к анализу несоответствий данная закономерность может быть сформулирована следующим образом: обычно 80% обнаруженных несоответствий связано лишь с 20% всех возможных причин.

Кроме выявления и ранжирования факторов но их значимости диаграмма Парето с успехом применяется для наглядной демонстрации эффективности тех или иных мероприятий в области обеспечения качества: достаточно построить и сравнить две диаграммы Паре-то — до и после реализации каких-либо мероприятий.

2. Причинно-следственная диаграмма предложена в 1953 г. К. Исикавой («диаграмма Исикавы»). Диаграмма представляет собой графическое упорядочение факторов, влияющих на объект анализа.

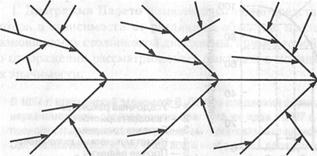
Главным достоинством диаграммы Исикавы является то, что она дает наглядное представление не только о тех факторах, которые влияют на изучаемый объект, но и о причинно-следственных связях этих факторов.

При построении диаграммы Исикавы к центральной горизонтальной стрелке, изображающей объект анализа, подводят большие первичные стрелки, обозначающие главные факторы (группы факторов), влияющие на объект анализа. Далее к каждой первичной стрелке подводят стрелки второго порядка, к которым, в свою очередь, подводят стрелки третьего порядка и т. д. до тех пор, пока на диаграмму не будут нанесены все стрелки, обозначающие факторы, оказывающие заметное влияние на объект анализа в конкретной ситуации. Каждая из стрелок, нанесенная на схему, в зависимости от ее положения представляет собой либо причину, либо следствие: предыдущая стрелка по отношению к последующей всегда выступает как причина, а последующая — как следствие.

Главная задача при построении диаграммы — обеспечение правильной соподчиненности во взаимозависимости факторов, а также четкое ее оформление.

При структурировании диаграммы на уровне первичных стрелок факторов во многих реальных ситуациях можно воспользоваться предложенным самим Исикавой правилом «пяти М» (материалы, машины, методы, измерения, люди). Это правило состоит в том, что в общем случае существует пять возможных причин тех или иных результатов, связанных с причинными факторами.

Детализированная диаграмма Исикавы может служить основой для составления плана взаимоувязанных мероприятий, обеспечивающих комплексное решение поставленной при анализе задачи.

3. Контрольная карта была предложена в 1924 г. У. Шухартом. Она строится на бланке (формуляре), на который нанесена сетка из тонких вертикальных и горизонтальных линий. По вертикали на карте отмечают выбранную статистическую характеристику наблюдаемого параметра (например, индивидуальное или среднее арифметическое значение, медиану, размах и др.), а по горизонтали — время или номер контрольной выборки. Так, на карту средних арифметических значений предварительно наносят: горизонтальную центральную линию, соответствующую значению центра допуска (ЦД) (при этом значении технологическая операция считается оптимально налаженной); две горизонтальные линии пределов установленного нормативной документацией технологического допуска (верхнего — Тв и нижнего — Тн); две горизонтальные линии, являющиеся границами регулирования значений контролируемого параметра (верхняя — Рв и нижняя — Рн). Границы регулирования ограничивают область значений регулируемой выборочной характеристики, соответствующей удовлетворительной наладке технологической операции (если контролируемый параметр задан односторонней нормой, то на контрольную карту наносится только одна граница регулирования). Для лучшего восприятия контрольной карты ее центральную линию и границы целесообразно обозначать разными цветами, например центральную линию — зеленым, допусковые границы — красным, границы регулирования — черным.

Границы регулирования рассчитываются с учетом принятого распределения значений контролируемого параметра и дополнительной вероятности получения ложного предупредительного сигнала о разладке операции. Доверительный интервал указывает, внутри каких границ ожидается истинное значение статистической характеристики.

Работа с контрольной картой сводится к тому, что по данным наблюдения за значениями контролируемого параметра устанавливается, находится ли этот параметр в границах регулирования, и на основании этого принимается решение о том, налажена ли технологическая операция или разлажена.

Решение о разладке операции принимается при выходе хотя бы одного наблюдения, фиксируемого на карте в виде точки, за границы регулирования. Однако еще до выхода точек за границы регулирования контрольная карта дает возможность судить о наметившихся нарушениях технологической операции по следующим признакам:

♦ вблизи границ регулирования появляются несколько последовательных значений контролируемого параметра;

♦ значения распределяются по одну сторону от центральной линии, т. е. среднее значение смещается относительно центра настройки (о наличии систематического отклонения свидетельствуют, например, расположение подряд семи значений выше или ниже средней линии, а также расположение 10 из 11, 12 из 14, 14 из 17 и 16 из 20 значений по одну сторону от средней линии);

♦ значения контролируемого параметра сильно разбросаны;

♦ намечается тенденция приближения значений контролируемого параметра к одной из границ регулирования.

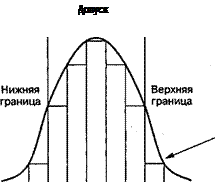4. Гистограмма представляет собой столбчатый график и применяется для наглядного изображения распределения конкретных значений параметра по частоте повторения за некий период времени (неделя, месяц, год).

При нанесении на график допустимых значений параметра определяется, как часто этот параметр попадает в допустимый диапазон или выходит за его границы.

Построение гистограммы ведется в следующей последовательности:

а) составляется таблица исходных данных;

б) оценивается размах анализируемого параметра;

в) определяется ширина размаха;

г) устанавливается точка отсчета первого интервала;

д) выбирается окончательное количество интервалов.

Вид гистограммы зависит от объема выборки, количества интервалов, начала отсчета первого интервала. Чем больше объем выборки и меньше ширина интервала, тем ближе гистограмма к непрерывной кривой.

5. Диаграмма разброса (диаграмма рассеивания) применяется для выявления зависимости одной переменной величины (показателя качества продукции, параметра технологического процесса, величины затрат на качество и т. п.) от другой. Диаграмма не дает ответа на вопрос о том, служит ли одна переменная величина причиной другой, но она способна прояснить, существует ли в данном случае причинно-следственная связь вообще и какова ее сила.

Наиболее распространенным статистическим методом выявления подобной зависимости является корреляционный анализ, основанный на оценке коэффициента корреляции. Взаимосвязь изучаемых величин может быть полной, т. е. функциональной, когда коэффициент корреляции равен единице (+1), если переменные одновременно возрастают или убывают, и (-1), если при возрастании одной переменной другая убывает. Примером функциональной связи может служить твердость материала заготовки: чем выше твердость, тем больше износ.

В том случае, когда взаимосвязь совсем отсутствует, коэффициент корреляции равен нулю. Возможен и промежуточный случай, когда зависимость связанных величин неполная, так как она искажена влиянием посторонних дополнительных факторов. Иллюстрацией подобного рода корреляционной связи может служить зависимость производительности труда рабочих от их стажа при воздействии таких дополнительных факторов, как образование, здоровье и т. д. Чем больше влияние этих дополнительных факторов, тем менее тесна связь между стажем и производительностью труда

Корреляционные связи описываются соответствующими уравнениями. В тех случаях, когда требуется выяснить зависимость одного параметра от нескольких других, применяется регрессивный анализ. Для выявления влияния отдельных факторов на исследуемый параметр применяется дисперсионный анализ, при котором исходят из того, что существенность каждого фактора в отдельных условиях характеризуется его вкладом в дисперсию результата эксперимента.

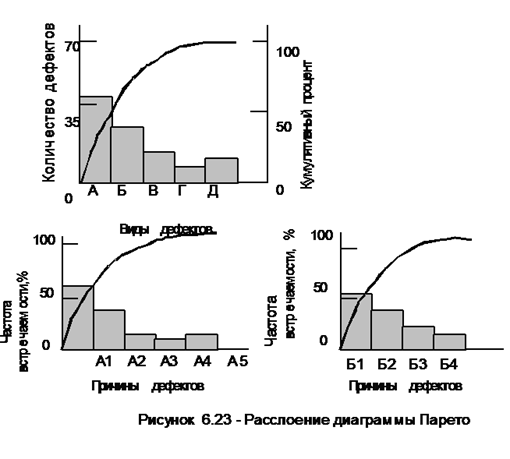
6. Метод расслоения (стратификации) применяется для выявления причин разброса характеристик изделия. Метод заключается в разделении (расслоении) полученных характеристик в зависимости от различных факторов: качества исходных материалов, методов работ и т. д. При этом определяется влияние того или иного фактора на характеристики изделия, что позволяет принять необходимые меры для устранения их недопустимого разброса.

На рис. 8.7.6 приведен пример расслоения диаграммы Парето по факторам А и Б при простейшем детальном анализе («распутывание связей») диаграммы. В данном случае расслоение позволяет получить представление о скрытых причинах дефектов.

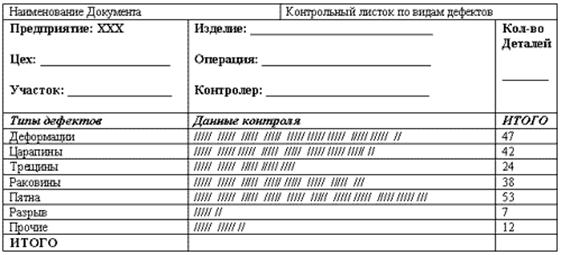
7. Контрольные листки применяются при контроле по качественным и количественным признакам. Контрольный листок представляет собой бумажный бланк, на котором приводятся названия контролируемых показателей и фиксируются их значения, полученные в процессе контроля.

Применяются следующие виды контрольных листков:

♦ контрольный листок для регистрации распределения измеряемого параметра в ходе производственного процесса;

♦ контрольный листок для регистрации видов несоответствий;

♦ контрольный листок для оценки воспроизводимости и работоспособности технологического процесса.

Дата добавления: 2014-01-20