Работа в электрическом поле. Потенциал

На рисунке 1.9 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение 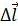. Работа Δ A кулоновских сил на этом перемещении равна

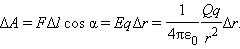
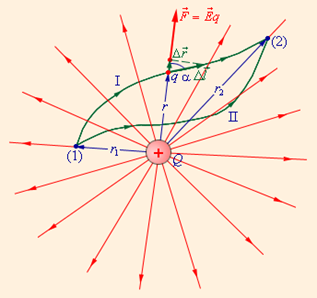Рисунок 1.9. Работа кулоновских сил при перемещении заряда q зависит только от расстояний r 1 и r 2 начальной и конечной точек траектории

Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δ r. Если это выражение проинтегрировать на интервале от r = r 1 до r = r 2, то можно получить (1.13) На траекториях I и II, изображенных на рисунке 1.9, работы кулоновских сил одинаковы. Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Из формулы (1.13) следует, что работа, совершаемая при перемещении заряда в электростатическом поле по замкнутому пути, равна нулю, т.е. 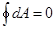. Если перемещённый заряд принять за единицу, то (1.13) можно записать в виде

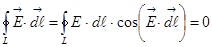или 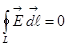. (1.14)

Этот интеграл называется циркуляцией вектора напряжённости вдоль замкнутого контура. Циркуляция вектора напряжённости вдоль замкнутого контура равна нулю. Отсюда следует, что линии напряжённости поля не могут быть замкнутыми. Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.

Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю. За опорную точку (0) удобно принять бесконечно удаленную точку

Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A₁₀, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0): W _p1 = A ₁₀.

(В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.)

Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0).

Работа, совершаемая электростатическим полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).

A ₁₂ = A ₁₀ + A ₀₂ = A ₁₀ – A ₂₀ = W _p1 – W _p2.

Потенциальная энергия заряда q, помещенного в электростатическое поле, пропорциональна величине этого заряда.

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

φ = , 1B = (1.14)

Потенциал φ является энергетической характеристикой электростатического поля.

Работа A ₁₂ по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ₁ – φ₂) начальной и конечной точек:

A ₁₂ = W _p1 – W _p2 = q φ₁ – q φ₂ = q (φ₁ – φ₂). (1.15)

Потенциал φ_∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

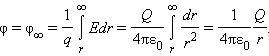(1.16)

Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.

Для наглядного представления электростатического поля наряду с силовыми линиями используют эквипотенциальные поверхности.

Рисунок 1.10. Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электростатического поля всегда перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рисунке 1.10 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей. В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.

1.5 Связь между и разностью потенциалов φ₁ – φ₂

Если пробный заряд q совершил малое перемещение 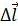вдоль силовой линии из точки (1) в точку (2), то можно записать:

Δ A ₁₂ = qE Δ l = q (φ₁ – φ₂) = – q Δφ,

где Δφ = φ₁ – φ₂ – изменение потенциала. Отсюда следует

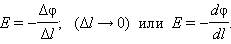(1.17)

Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии.

В более общем векторном виде вектор равен

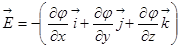, где 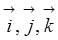– единичные векторы, направленные соответственно вдоль осей х, у, z Последнее уравнение можно записать в виде

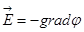или 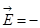Ñj, (1.18)

т.е. напряжённость поля равна градиенту потенциала и направлена в сторону убывания потенциала.

Дата добавления: 2014-01-20