
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема: Неопределённый интеграл
|
|
|
|
Лекция 5
Константы и переменные
Типы данных языка С
Ключевые слова
Язык программирования С
В 60е годы ОС Unix 1я была написана на языке С. Изначально язык создавался для решения системных задач. Популярность приобрёл благодаря разделению машинно независимых и зависимых свойств, то есть можно писать программы для различных видов маши не зависимо от архитектуры, памяти и процессора.
1989г. Был закреплён стандарт ANSI.
Достоинство языка:
1. Современность. Позволяет реализовывать структурное программирование, детализацию и т.д.
2. Эффективность. Получаются копактные и быстрые в исполнении программы.
3. Перемосимый и мобильный язык.
Алфавит языка С.
Состоит из 4х групп.
1. Латинский алфавит + подчёркивание. Строчные и прописные буквы имеют разные коды.
2. Цифры от 0 до 9.
3. Специальные символы.(.,;:!? ‘ | / ~ + - * () [] {} < > = ^ & % # “”)
4. Состовляют управляющие последовательности используемые при вводевыводе информации и начинаются они со знака.
Идентификатоы – это имя которым обазначаются некоторый объект в программе. Данные в памяти размещаются по адрессам, не известным программисту. Для того что бы программист имел к ним доступ используются идентификаторы, которые компилятором пеобразуются к адрессам в памяти. Для записи идентификатора используются латинские буквы, цифры, знак подчёркивания.
Правило записи:
1. Их имена не должны совпадать с зарезервированными и именами функции.
2. Не должныначинаться со знака подчёркивания.
Правильно выбранные идентификаторы облегчают понимание программы.
Ключевые слова – это имена используемые в С с заранее определённым смыслом их нельзя менять и к ним относятся auto do if sitceof break intcert
Необходимо различать типы данных. Существуют следующие базовые типы данных char int float double void
Char – символьный, занимает 1 байт.
Int – целый, занимает от 2 до 4 байт.
Float – вещественный, занимает 4 байта.
Double – вещественный с двойной точностью, занимает от 8 до 10 байт.
Void – пустой тип.
Существует 4 модификатора доступа sing unsing short long
Тип данных и модификатор определяют:
1. Формат хранения данных в памяти
2. Диапазон значений изменения переменных соответствующего типа.
3. Операции, которые могут выполняться над переменными типом.
Определение. Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается  интегралов функций.
интегралов функций.
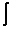 – значок интеграла.
– значок интеграла.
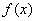 – подынтегральная функция. Знак интеграла используется для обозначения интеграла в математике. Впервые он был использован немецким математиком и основателем дифференциального и интегрального исчислений Лейбницем в конце XVII века.
– подынтегральная функция. Знак интеграла используется для обозначения интеграла в математике. Впервые он был использован немецким математиком и основателем дифференциального и интегрального исчислений Лейбницем в конце XVII века.
Символ (∫) образовался из буквы S (от лат. summa — сумма).
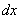 – значок дифференциала.
– значок дифференциала.
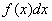 – подынтегральное выражение или «начинка» интеграла.
– подынтегральное выражение или «начинка» интеграла.
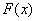 – первообразная функция.
– первообразная функция.
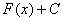 – множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа
– множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа 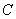 .
.
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
Решить интеграл – это значит найти определенную функцию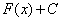 , пользуясь некоторыми правилами, приемами и таблицей.
, пользуясь некоторыми правилами, приемами и таблицей.
 Свойства неопределённого интеграла, непосредственно следующие из определения:
Свойства неопределённого интеграла, непосредственно следующие из определения:
1. 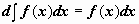 .
.
2. 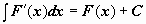 (или
(или 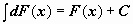 ).
).
3.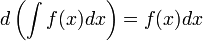
4. 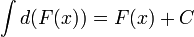
5. 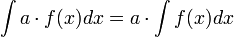
6.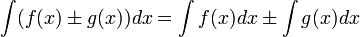
2. Если 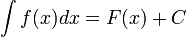 , то и
, то и 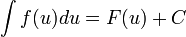 , где u = φ(x) — произвольная функция, имеющая непрерывную производную
, где u = φ(x) — произвольная функция, имеющая непрерывную производную
8.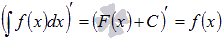
Производная результата интегрирования равна подынтегральной функции.
9.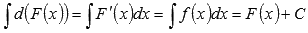
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
10.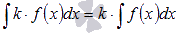 , где k – произвольная константа.
, где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.
Таблица неопределённых интегралов.
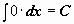 . .
| 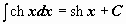 . .
| ||
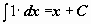 . .
| 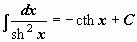 . .
| ||
 ( (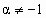 ). ).
| 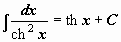 . .
| ||
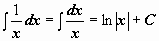 . .
| 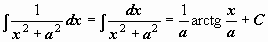 . .
| ||
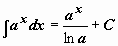 ; ;  . .
| 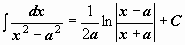 . .
| ||
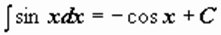 . .
| 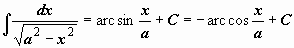
| ||
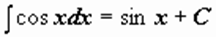 . .
| 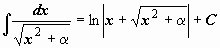 . .
| ||
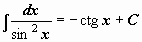 . .
| 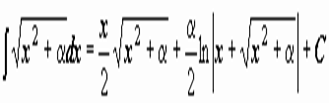 . .
| ||
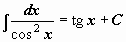 . .
| 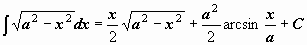 . .
| ||
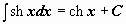 . .
| 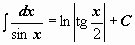 ; ; 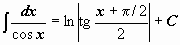 . .
|
Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:
- первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
- второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную.
Таким образом: Операция нахождения неопределенного интеграла называется интегрированием этой функции.
Самостоятельная работа:
Найти интегралы
1 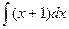 2
2 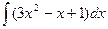 3
3 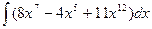 4
4 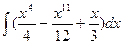
5 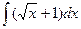 6
6 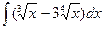 7
7 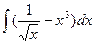 8
8 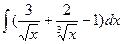
9 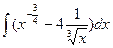 10
10 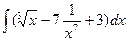 11
11 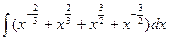 12
12 
12 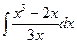 13
13 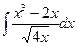 14
14 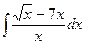 15
15 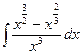 16
16 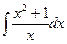 18
18 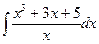
17 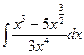 18
18 
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 396; Нарушение авторских прав?; Мы поможем в написании вашей работы!