
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Преобразование формул
|
|
|
|
Также, как и в исчислении высказываний, формулы ИП могут быть общезначимыми, выполнимыми (нейтральными) или невыполнимыми (универсально ложными). Вообще говоря, это можно проверить, построив таблицу истинности. Но как это сделать, если предикаты содержат переменные, значения которых в общем случае могут меняться неограниченно? Особенную сложность придает наличие кванторов. Доказать общезначимость при таких условиях совсем не просто. Более того, было показано, что вообще невозможно найти универсального метода установления факта общезначимости квантифицированных выражений, так что даже говорят о неразрешимости исчисления предикатов. Но все это - в общем случае. Практически выполнимость многих формул устанавливать удается, если обозначена область D, в которой связная переменная x принимает свои значения. Если при этом известны истинностные значения формул А (x) и B (x), то легко определяются значения и для формул 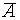 ,
, 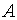
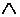
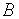 ,
, 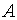
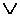
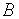 ,
, 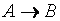 и др..
и др..
Формула 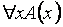 получает значение И, если А получает значение И для каждого x из D.
получает значение И, если А получает значение И для каждого x из D.
Формула 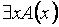 истинна, если А истинна хотя бы при одном значении x из D.
истинна, если А истинна хотя бы при одном значении x из D.
Пусть, например, х принимает значения в области D = (1,2,3), и известно, что A (1) = Л, A (2) = И, A (3) = Л. Формула 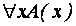 означает: для всех х А (х) истинна. Это условие у нас не выполняется, поэтому
означает: для всех х А (х) истинна. Это условие у нас не выполняется, поэтому 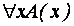 = Л. Формула
= Л. Формула 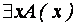 означает: существует х, при котором А (х) истинна. Очевидно, что здесь
означает: существует х, при котором А (х) истинна. Очевидно, что здесь 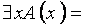 И.
И.
Были найдены процедуры, позволяющие устанавливать общезначимость некоторых ппф, в этом смысле стали говорить, что исчисление предикатов является полуразрешимым. Что же касается свободных переменных, то в большинстве случаев их достаточно конкретизировать, т.е. заменить на некоторые постоянные.
При преобразовании формул ИП используются те же приемы: снятие и ограничение отрицания, исключение импликации и эквивалентности, применение законов алгебры логики и правил равносильности и т.п.. При действиях со связками необходимо учитывать особенности квантификаций.
Пусть имеется формула А, не содержащая переменную х. Очевидно, в этом случае она не подпадает под действие квантора по х, т.е. 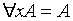 и
и  . Пусть теперь имеется формула В, содержащая свободную переменную х: B = B (x). Тогда справедливы следующие равносильности:
. Пусть теперь имеется формула В, содержащая свободную переменную х: B = B (x). Тогда справедливы следующие равносильности:
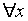 B (x)
B (x)  A =
A = 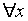 (B(x)
(B(x) A),
A),
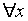 B (x)
B (x) 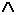 A =
A = 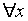 (B(x)
(B(x)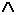 A),
A),
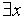 B (x)
B (x)  A =
A = 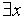 (B(x)
(B(x) A),
A),
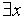 B (x)
B (x) 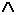 A =
A = 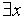 (B(x)
(B(x)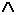 A). (6.3)
A). (6.3)
Если же формулы А и В обе содержат свободную переменную х, то справедливы равенства:
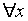 A (x)
A (x) 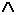
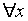 B (x) =
B (x) = 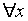 (A (x)
(A (x) 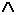 B (x)),
B (x)),
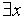 A (x)
A (x) 
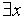 B (x) =
B (x) = 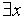 (A (x)
(A (x)  B (x)). (6.4)
B (x)). (6.4)
(Квантор  можно распределять по
можно распределять по 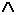 (И), квантор
(И), квантор  можно распределять по
можно распределять по  (ИЛИ)).
(ИЛИ)).
Дело осложняется, если требуется распределить квантор  по ИЛИ, а квантор
по ИЛИ, а квантор  по И. В этом случае равносильности, подобные (6.4), не выполняются. Тогда исходят из следующих соображений.
по И. В этом случае равносильности, подобные (6.4), не выполняются. Тогда исходят из следующих соображений.
Любая связанная переменная в ппф может принимать какие угодно наименования, так что можно написать, например:  хA (x) =
хA (x) =  zA (z) (то же и для
zA (z) (то же и для  ). Это действие называется переименованием переменных. Всегда стараются сделать так, чтобы каждому квантору соответствовала только одна переменная. Это значительно облегчает работу с кванторами. В дальнейшем мы будем широко этим пользоваться. Вот и в данном случае:
). Это действие называется переименованием переменных. Всегда стараются сделать так, чтобы каждому квантору соответствовала только одна переменная. Это значительно облегчает работу с кванторами. В дальнейшем мы будем широко этим пользоваться. Вот и в данном случае:
 xA (x)
xA (x) 
 xB (x) =
xB (x) = xA (x)
xA (x) 
 zB (z) =
zB (z) = x
x z (A (x)
z (A (x)  B (z))
B (z))
 xA (x)
xA (x) 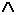
 xB (x) =
xB (x) = xA (x)
xA (x) 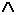
 zB (z) =
zB (z) = х
х z (A (x)
z (A (x) 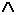 B (z)). (6.5)
B (z)). (6.5)
(При выносе кванторов за скобки теперь уже использовались соотношения (6.3), т.к. B (z), например, не зависит от x и т.п.).
Этот же прием можно использовать и в равенствах (6.4), т.е. справедливо:  xA (x)
xA (x) 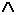
 xB (x) =
xB (x) = x
x z (A (x)
z (A (x) 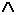 B (z)) и т.п..
B (z)) и т.п..
Здесь и в дальнейшем будем обозначать для удобства:
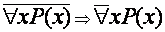 и
и 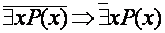 .
.
Из общего смысла квантификаций нетрудно понять следующие равенства преобразования отрицаний:
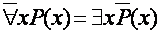 ;
; 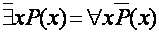 , (6.6)
, (6.6)
откуда легко получаются правила замены одного квантора другим:
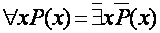 ;
; 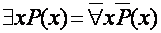 . (6.7)
. (6.7)
В процессе преобразований нам потребуются новые термины. Назовем литералом атом или его отрицание; дизъюнктом - дизъюнкцию литералов (в ИП это чаще называют предложением), матрицей - формулу, не содержащую квантификаций.
Если мы имеем матрицу, то дальнейшая работа с ней, в сущности, сводится к преобразованиям, аналогичным тем, которые мы проделывали с формулами исчисления высказываний. Да и цели-то бывают, в общем-то, те же: преобразование и представление в канонических (нормальных) формах, доказательство общезначимости (или невыполнимости), определение логического следствия (чаще всего по методу резолюций). Но для этого нужно научиться получать матрицу, т.е. научиться корректно переходить от формул с квантификациями к формулам, уже не содержащим никаких кванторов. Но сперва еще раз о переименованиях связных переменных, только более подробно.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 945; Нарушение авторских прав?; Мы поможем в написании вашей работы!