
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вывод в исчислении предикатов
|
|
|
|
Так же, как и в исчислении высказываний, проблема вывода в ИП сводится к проблеме дедукции, т.е. к решению вопроса: является ли формула В логическим следствием множества формул { E }. Напомним, что ппф B является логическим следствием множества { E }, если она принимает значение И всякий раз, как только все Еi одновременно принимают значение И. Вопрос решался через доказательство теоремы дедукции, которая справедлива и в ИП, с учетом, впрочем, ряда оговорок и условий, касающихся действий со связными и свободными переменными. Так же, как и в ИВ, встает проблема определения общезначимости той или иной формулы. И решается она примерно так же, т.е. как минимум пятью способами, каждый из которых применим в ИП:
1) оценка с помощью таблицы истинности,
2) оценка через преобразование, упрощение и приведение к нормальным формам,
3) оценка путем логического вывода из системы аксиом,
4) оценка методом редукции,
5) оценка методом опровержения.
Однако самым эффективным средством порождения и/или доказательства следствий здесь по-прежнему является метод резолюций.
В ИП резолюция применяется к предложениям, представляющим из себя дизъюнкцию литералов, каждый из которых, в общем случае, содержит различные переменные. Очевидно, что родительские предложения должны содержать контрарные литералы, идентичные по форме. Идентичность литералов достигается при этом применением соответствующих подстановок и унификации.
Пусть, например, у нас имеется два родительских предложения L и M, содержащие соответственно литералы l и 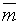 , которые допускают общую подстановку-унификатор s такую, что (l)s = (m)s (без учета инверсии). Теперь возможна резолюция, которая "уничтожит" оба этих литерала, но при этом надо помнить, что подстановка возможна только для предложения в целом. Поэтому результат резолюции можно записать в виде нового предложения, объединяющего (U) оставшиеся литералы:
, которые допускают общую подстановку-унификатор s такую, что (l)s = (m)s (без учета инверсии). Теперь возможна резолюция, которая "уничтожит" оба этих литерала, но при этом надо помнить, что подстановка возможна только для предложения в целом. Поэтому результат резолюции можно записать в виде нового предложения, объединяющего (U) оставшиеся литералы:
(L – l) s 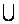 (M – m) s. (6.9)
(M – m) s. (6.9)
Родительских предложений может быть несколько, также как и пар контрарных литералов. Резольвенту (6.9) перепишем теперь в общем виде:
(L – { li }) s 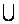 (M – { mi }) s. (6.10)
(M – { mi }) s. (6.10)
Рассмотрим следующий пример. Имеется два предложения:
L: P [ x,f (A)]  P [ x,f (y)]
P [ x,f (y)]  Q (y),
Q (y),
M: 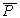 [ z,f (A)]
[ z,f (A)] 
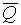 (z).
(z).
Для резолюции выбираем литералы: l=P [ x,f (A)] и m=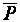 [ z,f (A)].
[ z,f (A)].
Подстановка s = z/x для них является унификатором (применяя ее к l). Но при этом все предложение L примет вид:
Lа: P [z,f(A)] P [z,f(y)]
P [z,f(y)] Q(y).
Q(y).
Результат резолюции La и М согласно (6.9):
P[z,f(y)] Q(y)
Q(y)
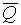 (z).
(z).
Совершенно иной результат получится, если выбрать множество { li } = (P [ x,f (A)], P [ x,f (y)]), а m =`P [ z,f (A)].
Введем унификатор s = (z/x, A/y). Исходные предложения принимают вид:
Lb: P [ z,f (A)]  P [ z,f (A)]
P [ z,f (A)]  Q (А),
Q (А),
M: 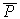 [ z,f (A)]
[ z,f (A)] 
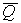 (z).
(z).
Два первых литерала предложения Lb склеиваются в один, и в результате получится резольвента Q (A) 
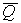 (z).
(z).
Здесь возможны и другие резолюции, в частности, по Q.
Примечание. Термы в многоместном предикате не могут меняться местами, поэтому литералы P (x,f (y)) и P (f (y) ,x) не идентичны. Это следует учитывать в процессе резолюции.
Так же, как и в исчислении высказываний, метод резолюций - основной инструмент доказательства логического следствия по методу опровержения. Принцип дедукции, который при этом реализуется, все тот же: если ппф В является логическим следствием системы { E }, то справедливо { E,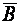 }
} 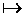 Л, т.е. множество { E,
Л, т.е. множество { E, } имеет своим следствием пустой дизъюнкт. Надо только помнить, что все формулы здесь - ппф в смысле исчисления предикатов со всеми вытекающими отсюда действиями и ограничениями.
} имеет своим следствием пустой дизъюнкт. Надо только помнить, что все формулы здесь - ппф в смысле исчисления предикатов со всеми вытекающими отсюда действиями и ограничениями.
Пусть заданы две гипотезы:
1.  x [ P (x)
x [ P (x) 
 xQ (x)
xQ (x)  R (x)],
R (x)],
2. `"yQ (y).
Требуется доказать, что выражение
3.`$ zP (z) 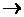
 zR (z)
zR (z)
является логическим следствием этих двух. Следуя принципу дедукции, находим отрицание выражения 3:
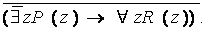
Исключая импликацию и приводя в порядок отрицания, получаем:
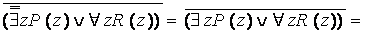
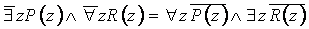
(после переименования и сколемизации – к предваренной форме),
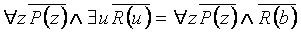 .
.
Или окончательно:
4. 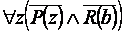 .
.
Гипотеза 1 преобразуется просто (вводится функция Сколема):
5.  x[P(x)
x[P(x)
 wQ(w)
wQ(w) R(x)]=
R(x)]= x[P(x)
x[P(x) Q(g(x))
Q(g(x)) R(x)],
R(x)],
а для гипотезы 2 используем равенство:
6. 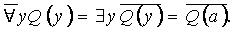
Кванторы общности в предваренных формах выражений 4 и 5 теперь можно опустить. Мы приходим к системе предложений
a) P (x)  Q (g (x))
Q (g (x))  R (x),
R (x),
б) 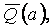
в) 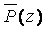 ,
,
г) 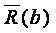 .
.
(Знак 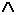 в матрице выражения 4 опускается, и она распадается на два предложения в) и г)).
в матрице выражения 4 опускается, и она распадается на два предложения в) и г)).
Теперь можно проводить резолюции. У каждой резольвенты будем указывать унификатор, позволяющий ее получить.
д) Q (g (z)) R (z), s = z / x (а, в)
R (z), s = z / x (а, в)
Q (g (B)), s = B / z (г, д),
ж) Л, s = A / g (B) (б, е).
Логическое следствие доказано.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 923; Нарушение авторских прав?; Мы поможем в написании вашей работы!