Подстановки и унификация

Пусть имеется формула P (x,y,z). Ввести подстановку s это значит определить множество пар типа s = { t₁/x, t₂/y, t₃/z },позволяющих заменить x на t₁, y на t₂, z на t₃ во всех местах их вхождений. Полученная формула равносильна прежней: P (x,y,z) = P (t₁, t₂, t₃).

Подстановки открывают широкие возможности при преобразовании формул. Простейший пример:

дана формула P (x,f (y) ,z) 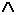P (а,b,r).

Введем подстановку s₁ = { а/x,b/f(y),r/z } для первого предиката и получим: P (а,b,r) 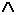P (а,b,r) = P (а,b,r), т.е. произошла "склейка" - распространенный прием в процессах вывода.

Проводя подстановки, надо следовать следующим правилам:

¨ подстановки применяются только для свободных переменных, в том числе и для функциональных, во всех местах их вхождений в данную формулу (предложение);

¨ переменную можно заменить константой, но нельзя константу заменить переменной;

¨ переменная не может быть заменена на терм, содержащий ту же самую переменную;

¨ подстановки могут касаться только некоторых термов предиката, остальные термы остаются без изменения;

¨ одна функция не может подставляться вместо другой, но может заменять переменную-аргумент;

¨ нельзя вместо свободной переменной ввести уже связанную, другими словами, вводимое подстановкой вхождение переменной не должно попадать в область действия квантора, связывающего данную переменную.

К последнему правилу приведем простой пример. Формула y (x<y) отображает вполне корректное математическое условие (для любого х всегда найдется y, что x < y). Некорректная подстановка y/x приводит к ложному суждению: y (y < y).

Если к формуле Е применена подстановка s₁, тo пишут Еs₁. Так, если к предикату P (x,f (y) ,B) применена подстановка s₁ = { z/x,w/y }, то можно написать P (x,f (y) ,B) s₁ = P (z,f (w) ,B).

Если к полученной формуле применить еще подстановку s₂= { C/z, D/f (w)}, то получится P (x,f (y) ,B) s₁s₂ = P (C,D,B).

Если все термы предиката не содержат переменных, то мы имеем "основной частный случай" ("основной пример").

Последовательное применение подстановок называется их композицией.

Некоторая подстановка s называется унифицированной (унификатором), если ее применение к ряду формул E₁,E₂,,... делает их равными: E₁s = E₂s = E₃s... Например, подстановка s = { A/x,B/y } унифицирует формулы P (x,f (y) ,B) и P (x,f (B) ,B) и дает P (A,f (B) ,B).

Примечание. Обратите внимание, что предикатные символы при этом должны быть одинаковыми.

Освоить технику унификации совершенно необходимо. В процессе резолюции, например, контрарные литералы должны быть идентичны, что как раз и достигается их унификацией. Разберем поэтому несколько показательных примеров.

Пример 1. Унифицировать множество литералов:

{ P (a,x), P (y,f (b))}.

Поиск возможных подстановок начинаем с установления различий в термах обоих литералов, начиная с левых позиций. Первое рассогласование: (a,y). Tак как переменной здесь является y, то вводим подстановку s₁= (а/y). Получаем пару литералов

{ P (a,x), P (a,f (b))}.

Очередное рассогласование: (x,f (b)). Теперь уже вводим подстановку s₂ = (f (b) /x): { P (a,f (b)), P (a,f (b))}. Унификация состоялась. Общая подстановка имеет вид su = s₁s₂ = (a/y, f (b) /x).

Подстановка su, определенная таким образом, называется наиболее общим унификатором - ноу.

Пример 2. Определить ноу для пары литералов

P(x,f(x),z) и P(A,u,u).

Начинаем с левых позиций. Рассогласование: (x,A), подстановка
s₁ = (A/x), литералы: P (A,f (A) ,z) и P (A,u,u). Рассогласование: (f (A) ,u),
s₂ = (f (A) /u), литералы: P (A,f (A) ,z) и P (A,f (A) ,f (A)). Рассогласование: (z,f (A)), s₃ = (f (A) /z).

Окончательно:

P(A,f(A),f(A)) и P(A,f(A),f(A)).

Наиболее общий унификатор su = s₁s₂s₃ = (A/x,f (A) /u,f (A) /z).

Дата добавления: 2014-01-20