
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Ньютона. Решение уравнений с одной переменной
|
|
|
|
Пусть требуется решить уравнение 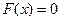 (1), где функция
(1), где функция 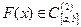 – дважды непрерывно-дифференцируема на
– дважды непрерывно-дифференцируема на 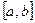 ;
; 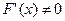 на
на 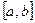 и
и 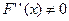 и
и 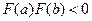 .
.
Из этих условий вытекает, что на 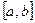 функция имеет только один корень.
функция имеет только один корень.
Прежде, чем использовать итерации, необходимо (1) привести к виду  .
.
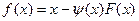 .
.
Функция 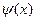 непрерывная в окрестности корня
непрерывная в окрестности корня 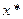 уравнения (1). Следовательно, уравнение (1) и уравнение
уравнения (1). Следовательно, уравнение (1) и уравнение 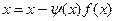 (2) будут иметь один и тот же корень
(2) будут иметь один и тот же корень 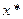 .
.
В качестве 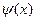 выберем
выберем  , тогда
, тогда 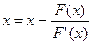 (3)
(3)
Выберем начальное приближение 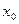 достаточно близкое к
достаточно близкое к 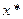 . Остальные приближения получаются по формуле:
. Остальные приближения получаются по формуле:
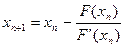 (4)
(4)
Метод, определенный (4), называется методом Ньютона.
Докажем, что метод Ньютона сходится и получим его оценку погрешности.
Если дано, что 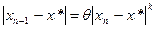 , где , где 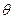 – символ Ландау: – символ Ландау:
|
| · если k=1, то скорость сходимости линейная; |
| · если k=2, то скорость – квадратичная; |
| · если k=3, то скорость – кубическая; |
| · если k>1, то сходимость метода сверхлинейная. |
Докажем, что (4) сходится.
Для этого покажем, что отображение 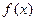 – сжатие, где
– сжатие, где 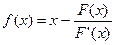 .
.
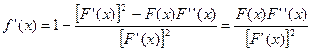 .
.
При  получим
получим
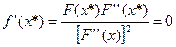 .
.
По непрерывности функции 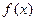 на
на 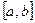 существует такая окрестность точки
существует такая окрестность точки 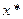 , что для
, что для  ,
, 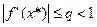 , а этом сжатие.
, а этом сжатие.
Поэтому к отображению 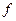 можно применить принцип сжатыхотображений.
можно применить принцип сжатыхотображений.
Если выбрать 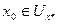 , то
, то 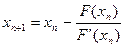 будет сходиться к точному решению
будет сходиться к точному решению 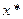 уравнения (1)., т.е.
уравнения (1)., т.е. 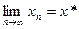 .
.
Заметим, что метод (4) будет сходиться, если начальное приближение 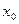 будем выбирать из окрестности
будем выбирать из окрестности 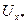
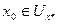 ,
, 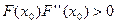 .
.
Докажем, что метод Ньютона сходится.
Определим скорость сходимости метода Ньютона. Для этого  разложим в ряд Тейлора в точке
разложим в ряд Тейлора в точке  .
.
 .
.
При  имеем
имеем  . Поэтому
. Поэтому
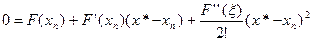
Выразим 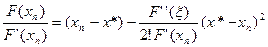 (5)
(5)
 Обозначим через
Обозначим через 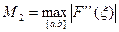 ,
, 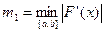
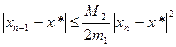 (6)
(6)
 , скорость сходимости метода Ньютона квадратичная,
, скорость сходимости метода Ньютона квадратичная, 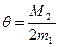 .
.
Потребуем, чтобы начальное условие 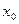 выбиралось из условия
выбиралось из условия
 (7)
(7)
Тогда из (6) получим


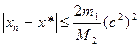 - оценка погрешности.
- оценка погрешности.
Метод Ньютона имеет квадратичную скорость сходимости. Это означает, что при переходе от одной итерации к другой количество верных знаков удваивается в последующем приближении.
Достоинство: высокая скорость сходимости, легко программируется на ЭВМ.
Недостатки: узкая область сходимости.
Если будем решать операторное уравнение 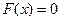 , то на каждом шаге необходимо находить значение обратного оператора
, то на каждом шаге необходимо находить значение обратного оператора  .
.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 550; Нарушение авторских прав?; Мы поможем в написании вашей работы!