Интервальные оценки истинного значения

Оценки истинного значения на основании ограниченного ряда наблюдения.

Композиция законов распределения.

Распределение гармонического колебания

Обозначение КТ в документации на СИ

Погрешности, обусловленные взаимодействием СИ и объекта измерения (ОИ).

Погрешности измерений.

Согласно ГОСТ 8.009-84следует различать четыре составляющие погрешности средств измерения:

- основную

- дополнительную

- погрешность, обусловленную взаимодействием средств и объекта измерения

- динамическая

Основная погрешность обусловлена не идеальностью собственных свойств средств измерения и показывает отличие действительной функции преобразования средств измерения в н.у. от номинальной функции преобразования. По способу числового выражения основной погрешности различают абсолютную, относительную, приведенную погрешность.

Абсолютная – это разность между показаниями прибора – Х и истинным значением А измеряемой величины Δ=Х-А.

Абсолютная погрешность взятая с обратным знаком называется поправкой.

Π= -Δ

Относительной погрешностью ИП, называется отношение абсолютной погрешности к истинному значению ИВ:

δ = %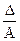

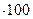Относительная погрешность обычно существенно изменяется вдоль шкалы аналогового прибора. С увеличением значения ИВ она увеличивается.

Приведенной погрешностью ИП, называется отношение абсолютной погрешности к нормированному значению.

%

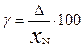Основной погрешностью ИП, называется погрешность при нормальных условиях работы ИП.

По характеру влияния на функцию преобразования основной погрешности ИП можно представить в виде:

- аддитивной составляющей

- мультипликативной составляющей

Δ

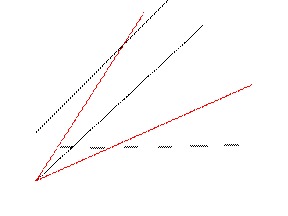
х

Аддитивная не зависит от чувствительности прибора и является постоянной для всех значений входной величины в пределах диапазона измерения.

Мультипликативная зависит от чувствительности прибора и изменяется пропорционально текущему значению входной величины.

Суммарная абсолютная погрешность выражается уравнением:

Δ=a + b,

т.е аддитивная и мультипликативная составляющие присутствуют одновременно. Для аддитивной – помехи, шумы, погрешность дискретности (квантования) для цифрового прибора.

Если прибору присуща только аддитивная погрешность или она существенно превышает все остальные составляющие, то целесообразно нормировать Δ.

К мультипликативной относят погрешности изготовления шунта в амперметре, добавление сопротивления в вольтметре, а также различные коэффициенты деления. Мультипликативная составляющая Δ увеличивается с увеличением входной величины, а т.к. относительная погрешность остается постоянной, то в этом случае целесообразно нормировать погрешность прибора в виде δ.

Аддитивная и мультипликативная погрешности могут иметь систематический и случайный характер.

Систематическая погрешность СИ – это составляющая погрешности, остающаяся постоянной или закономерно изменяющаяся при многократных измерениях одной и той же величины.

К постоянной систематической погрешности относят градуировки шкалы аналоговых приборов; калибровки цифровых приборов; погрешности, обусловленные не точностью подгонки резисторов; температурные изменения параметров электрических токов приборов и т.д.

К переменной систематической погрешности относят погрешности, обусловленные нестабильностью напряжения источника питания, влиянием электромагнитных полей и т.д.

Случайная погрешность СИ – это составляющая погрешности, изменяющаяся случайным образом. Она возникает из – за нестабильности переходящего сопротивления в контактах коммутативных устройств; трения в опорах подвижной части прибора.

При определении основной погрешности у СИ, абсолютная погрешность может быть представлена ее составляющими – систематической и случайной.

Дополнительная погрешность обусловлена реакцией СИ на изменение внешних, влияющих величин и неинформативных параметров входного сигнала. Входной сигнал не используется для передачи значений ИВ.

Дополнительная погрешность зависит от свойств СИ и от изменения, влияющих величин отличных от нормальных.

Нормальные условия эксплуатации СИ:

- t_{ок.возд.}= 20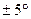С;

- относительная влажность 30% ÷ 80%;

- атмосферное давление 630 ÷ 795 мм рт.ст.;

- напряжение питания сети 220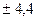В;

- частота питания сети 50Гц;

и т.д.

Подключение СИ к ОИ во многих случаях приводит к изменению значения ИВ, относительно того значения, которое она имела до подключения СИ к ОИ и, определение которой является целью измерения. Эта составляющая зависит так же от свойств СИ и свойств ОИ.

Динамические погрешности, обусловлены реакцией СИ на скорость, частоту изменения входного сигнала. Зависит от динамических свойств СИ, от частотного спектра входного сигнала, изменений нагрузки, влияющих факторов, величин. На выходной сигнал СИ влияют значения входного сигнала и любые изменения его во времени.

Различают полную и частную динамические характеристики.

Полная динамическая характеристика – эта характеристика полностью описывает принятую математическую модель динамических свойств СИ и однозначно определяет изменение выходного сигнала СИ при любом изменении во времени информативного или не информативного параметра входного сигнала, или влияющих величин.

Полную динамическую характеристику аналоговых СИ выбирают из следующих характеристик:

1) Дифференциальное уравнение;

2) Передаточные функции;

3) Импульсной и переходной характеристикой

4) Амплитудно-фазовой характеристикой

5) Амплитудно-частотной характеристикой

Частная динамическая характеристика – это любой функционал или параметр полной динамической характеристики.

К частным динамическим характеристикам аналоговых СИ можно отнести:

- время реакции

- коэффициент демпфирования

- значение АЧХ на резонансной частоте

КЛАСС ТОЧНОСТИ И НОРМИРОВАНИЕ ПОГРЕШНОСТЕЙ

В разных точках диапазона СИ погрешность принимает различные значения. Необходимо нормировать предел допускаемой погрешности, следовательно, устанавливают какие – то границы, за пределы которых, погрешность не должна выходить, ни при изготовлении прибора, ни при его эксплуатации. Сами пределы допускаемой погрешности СИ электрических величин установлены ГОСТ 8.401 – 80, в виде абсолютной, относительной и приведенной погрешности.

Длясопоставления СИ, предназначенного для измерения одной и той же ФВ, служит класс точности (КТ).

КТ СИ – это обобщенная характеристика, определенная пределами, допускаемых основных и дополнительных погрешностей, а так же другими свойствами, влияющими на точность, значения которых устанавливают в стандартах на отдельные виды СИ.

КТ характеризует свойства приборов в отношении точности, но не является непосредственным показателем точности измерения, т.к. точность измерения зависит еще от метода измерения и от условий, при которых выполняется измерение. Пределы допускаемых основных и дополнительных погрешностей, следует выражать в форме приведенных относительных или абсолютных погрешностей, в зависимости от характера изменения погрешности в пределах диапазона измерения, а так же от условий применения и назначения СИ конкретного вида. Пределы допускаемых дополнительных погрешностей, иногда можно выражать в форме отличной от формы выражения пределов основных погрешностей.

НОРМИРОВАНИЕ ПОГРЕШНОСТЕЙ

В зависимости от вида погрешности СИ различают несколько способов нормирования погрешности:

1) Если аддитивная погрешность СИ, преобладает над мультипликативной, то удобнее нормировать абсолютную или приведенную погрешность, т.к. нормирующее значение в этом случае выражается одним числом:

Δ=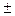а, где а – число

Δ

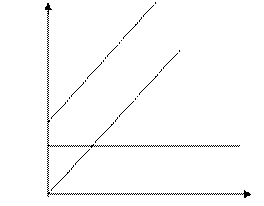Δ=а+b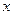

Δ=b

Δ=const

х

Предел допускаемой относительной погрешности будет изменяться по гиперболе (кривая 3)

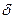
Кривая 3

х

Нормирование по абсолютной погрешности не позволяет сравнивать с разными диапазонами измерения по точности, поэтому принято нормировать приведенную погрешность:

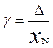=,где

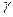- пределы допускаемой основной погрешности в %;

Δ – пределы допускаемой абсолютной погрешности;

х_N – нормированное значение, выраженное в тех же единицах, что и Δ;

Р – отвлеченное положительное число, выбираемое из ряда: 1∙10⁴; 1,5∙10⁴ ; 2∙10⁴ ; 2,5∙10⁴ ; 4∙10⁴ ; 5∙10⁴ ; 6∙10⁴.

n = 1; 0; -1; -2; и т.д.

Нормированное значение Х_N принимают равным:

а) Конечному значению шкалы прибора, если нулевая отметка прибора находится на краю или вне шкалы прибора.

б) Когда оно равно номинальному значению, если прибор предназначен измерению величины, имеющие номинальные значения.

в) Арифметической сумме конечных значений диапазона измерения, если прибор имеет двустороннюю шкалу:

₀

-Х_N Х_N

г) Длине шкалы, если шкала резко нелинейная.

Приведенные основные погрешности позволяют сравнивать по точности приборы, имеющие разные пределы измерения, но она не применяется как характеристика погрешности результата измерения.

2) Если мультипликативная преобладает над аддитивной, то нормируется предел допускаемой относительной погрешности, т.к. последняя будет постоянной по всему диапазону измерения

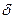
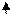
х

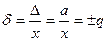, где q - отвлеченное положительное число, выбираемое из ряда, приведенного для р.

3) Для СИ с аддитивной и мультипликативной погрешностями, нормируют предел допускаемой относительной погрешности.

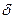
х

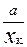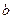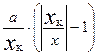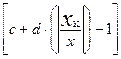=- += =+=, где

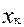- конечное значение диапазона измерения;

с,d >0, положительные постоянные члены;

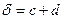, при условии, что ;

, при условии, что .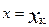

Т.о. с – предел допускаемой относительной погрешности, при максимальном показании прибора.

Данная формула используется при нормировании погрешности СИ высокой точности. В частности цифровых приборах многозначных мер сопротивления.

КТ СИ, у которого аддитивная и мультипликативная составляющие основной погрешности соизмеримы, обозначается отношением . Числа c и d выбираются из того же ряда, что и p.

Погрешности СИ при нормировании округляются до двух значащих цифр. Дополнительная погрешность выражаются в таком же виде как и основная, причем для различных влияющих величин нормируются отдельно.

Для СИ устанавливаются пределы допускаемых отклонений, каждой влияющей величины от нормальной. За пределами нормального диапазона, но в пределах рабочей области, погрешности СИ складываются из основной Δ и дополнительных, вызванных изменением i-ой величины.

Δ_∑=Δ+

Если пределы допускаемой погрешности СИ, задается в виде графиков, таблиц, какой – то более сложной формы, то классы точности обозначаются римскими цифрами или прописными буквами латинского алфавита.

Форма выражения основной погрешности	Расчет допускаемой основной погр. по формуле	Пределы допускаемой основной погрешности, %	Обозначение КТ
В документации	На СИ
Приведенная основная погрешность	-СИ равном -СИ неравном		КТ 1,5 КТ 1,5	1,5 1,5 ˇ
Относительная основная погрешность		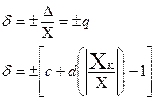	КТ 0,5 КТ 0,02/0,01	(0,5) 0,02/0,01
Абсолютная основная погрешность	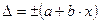или по сложной формуле	—	КТ:М	М
Относительная основная погрешность	По сложной формуле. Таблицы, графики	—	КТ:С	С

ПУТИ ПОВЫШЕНИЯ ТОЧНОСТИ СИ.

1) Стабилизация важных параметров элементов и узлов СИ техническим путем или использование материалов с малой зависимостью свойств от внешних факторов.

2) Методы защиты СИ от быстроизменяющихся влияющих величин, т.е. уменьшение случайной погрешности путем фильтрации, теплоизоляции, экранировка, амортизации и т.д.

3) Стабилизация медленно изменяющихся влияющих величин

4) Методы коррекции составляющих систематической погрешности (аддитивной, мультипликативной) от погрешности нелинейности

5) Методы статистической минимизации обработки результатов наблюдения при наличии случайной погрешности.

СЛУЧАЙНЫЕ ПОГРЕШНОСТИ ИЗМЕРЕНИЯ

И СПОСОБЫ ИХ ОПИСАНИЯ.

Количественная оценка степени достоверности результатов измерения, заключается в установлении количественной меры близости между случайным результатом измерения и неизвестным истинным значением. Результаты каждого i-ого наблюдения непредсказуемы из – за наличия случайной погрешности. Поэтому описание результатов наблюдения и самой случайной погрешности может осуществляться только на основе теории вероятности и математической статистики.

Погрешность Δ, как случайная величина наиболее полно характеризуется функцией распределения вероятностей F(Δ) (интегральный закон распределения), определяет вероятность появления того, что случайная погрешность Δ_i в i-ом опыте окажется меньше некоторого значения Δ.

F(Δ)= Р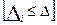=Р(<Δ_i 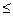Δ), где Р – вероятность события.

Обычно F(Δ), графически представляет собой неубывающую функцию, вероятность, которой изменяется 0÷1. Зная вероятность появления Δ_i различных значений, можно построить распределение вероятности появления погрешности в функции этого значения.

F(Δ)→F(-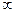)=0; F(+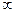)=0

F(Δ)

А

0,5

0 Δ_А Δ

Если функция появления вероятности распределения Р симметрична относительно т.А, соответствующей вероятности 0,5; то распределение результата измерения будет симметрично относительно истинного значения т.А. В этом случае целесообразно F(Δ) сдвинуть по оси абсцисс на значение Δ_А=Δ_с, т.е исключается систематическая составляющая погрешности и получается в результате функция распределения только случайной составляющей Δ=.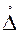

Функция распределения Р погрешности Δ отличается от функции распределения Р случайной составляющей погрешности, только сдвигом по оси абсцисс на Δ_с.

Вероятность попадания случайной погрешности в заданный интервал (Δ₁ 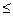Δ<Δ₂) равна приращению F(Δ) на этом интервале:

Р(Δ₁ 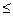Δ<Δ₂)=F(Δ₂)-F(Δ₁).

При сужении интервала (Δ₂ →Δ₁) вероятность Р→0. Для описания погрешности, как случайных величин наряду с F(Δ) вероятности, применяется плотность распределения вероятностей (дифференциальный закон) f(Δ):

f(Δ)=.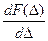

Из этого выражения следует, что f(Δ) и F(Δ) связаны интегрально:

F(Δ)=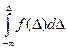

График плотности распределения может иметь различную форму в зависимости от закона распределения погрешности. Для F(Δ) кривая f(Δ) имеет форму близкую к форме колокола:

f(Δ) m_x

Δ

Δ₁ Δ_c Δ₂

В случае, если погрешность Δ имеет две составляющие, причем случайные погрешности группируются около систематической. Малые случайные имеют большую плотность, нежели большие случайные. Т.к. F(Δ)=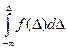, то вероятность появления случайных погрешностей определяется площадью, ограниченной кривой f(Δ) или ее частью и осью абсцисс, в зависимости от рассматриваемого интервала погрешности.

Р(Δ₁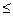Δ<Δ₂)=F(Δ₂)-F(Δ₁)=

Значение f(Δ)dΔ есть элемент вероятности, равный площади прямоугольника с основанием dΔ и абсциссами Δ₁, Δ₂, называемыми квантилями, т.к. F(+=1, то справедливо равенство:

- правило нормировки.

Т.е площадь под кривой f(Δ) согласно правилу нормировки равна 1 и отражает вероятность всех возможных событий..

(Δ_1, Δ₂) – доверительный интервал. Доверительный интервал случайной погрешности, ограниченный квантилями Δ₁, Δ₂, охватывает вероятность всех возможных значений случайной погрешности, а обратная величина q=1-p остается за границами этого интервала (q – вероятность противоположного события или уровень значимости).

Со статистической позиции можно дать следующее определение составляющей погрешности:

Систематическая погрешность (Δ_с) – это отклонение математического ожидания (m_x) результата наблюдения от истинного значения А измеряемой величины:

Δ_с=m_x- А

Δ_с=m_x-А=М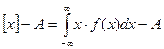

М- дискретных величин.

Случайная погрешность(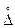) – разность между результатом единичного наблюдения и математического ожидания результатов:

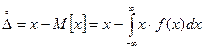
Математическое ожидание погрешности – равно математическому ожиданию систематической составляющей погрешности, т.к. математическое ожидание случайной погрешности всегда равно 0:

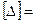ММ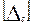, т.к. М

АКСИОМЫ РАСПРЕДЕЛЕНИЯ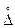

1) При очень большом числе измерений, случайные погрешности одинаковые по величине, но разные по знаку, встречаются одинаково часто.

2) Малые погрешности встречаются чаще больших. Очень большие погрешности встречаются крайне редко.

3) 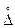проявляется, как сумма большого числа воздействий внешних факторов, малых эффектов, отделить, которые друг от друга практически невозможно (закон больших чисел).

ЧИСЛОВЫЕ, ВЕРОЯТНОСТНЫЕ ХАРАТЕРИСТИКИ

СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ.

Вероятностной характеристикой 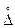, как случайных величин является закон распределения вероятностей, позволяющий оценить вероятность появления погрешности разных значений и f(Δ) с которой распределяется значение.

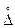Реальные законы распределения определяются при разработке новых методов и средств измерения, при ответственных измерениях, т.к. связан с большим объемом наблюдений и сложной математической обработкой. Чтобы характеризовать 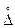, часто пользуются некоторыми числовыми, вероятностными характеристиками 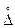, которые называются начальным и центральным моментом распределения (мат. Ожидание, дисперсия, СКО, коэффициент ассиметрии, эксцесс).

Моменты представляют собой некоторое среднее значение и называются начальными, если усредняются величины, отсчитываемые от начала координат и центральными, если они отсчитываются от центра функции f(Δ).

Все моменты, и начальный, и центральный имеют порядок (r).

Начальные моменты порядка r, результата наблюдений случайных величин Х, представляет собой математическое ожидание х^r.

, где

- начальные моменты.

Из данного выражения следует, что первый начальный момент 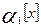совпадает с математическим ожиданием результата измерения:

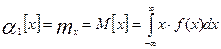
Математическое ожидание является оценкой истинного значения измеряемой величины.

Центральным (центрированным) моментом r-ого порядка называется интеграл вида:

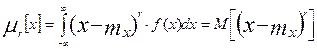, который получают при смещении начала координат f(Δ) в т.m_x.

Первый центральный момент результатов наблюдения равен 0, а второй центральный момент (дисперсия результатов наблюдения):

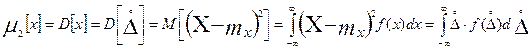
Дисперсия случайной погрешности равна дисперсии результатов наблюдения и является характеристикой их рассеивания, относительно математического ожидания.

Дисперсия увеличивается с увеличением рассеивания результатов наблюдения.

В качестве характеристики рассеивания используют среднеквадратичное отклонение результатов наблюдения, т.е.:

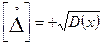
Для более подробного описания распределения используются моменты более высокого порядка.

Третий центральный момент характеризует ассиметрию распределения центральных погрешностей.

f()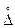

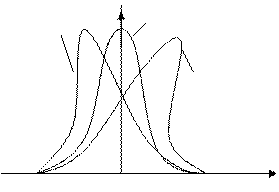S_k=0

S_k>0

S_k<0

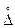
S_k=.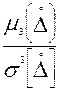

Четвертый центральный момент характеризует форму (плосковершинность или островершинность) распределения 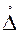и описывается с помощью эксцесса:

f()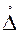

E_k>0 E_k=0

E_k<0

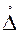
Е_k=.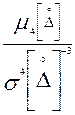

Число 3 вычитается, т.к. для нормального распределения 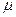порядка 4 случайной величины равно 3, т.е. 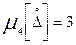, следовательно эксцесс Е_k=0.

Выражение - контрэксцесс.

Рассмотренные числовые характеристики являются основными.

НАИБОЛЕЕ ИЗВЕСТНЫЕ ЗАКОНЫ

РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.

1) Равномерный закон распределения:

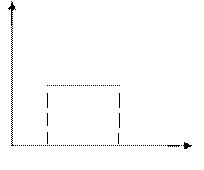f()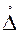

a b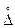

Плотность распределения:

f(X)=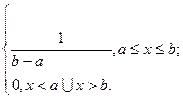 где a = const, b=const.

Математическое ожидание:

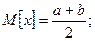
Дисперсия:

.

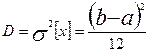Равномерное распределение характерно для не исключенной систематической погрешности.

Если отсутствуют данные о виде распределения систематической погрешности, то они принимаются равномерными, т.к. оцениваются границами допускаемых погрешностей.

2) Нормальное распределение Гаусса:

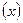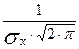
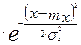
f=- для случайных величин, меняющихся .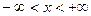

Математическое ожидание:

На практике часто используют стандартное нормальное распределение:

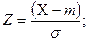
Плотность распределения:

, .

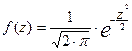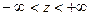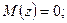
Дисперсия:

.

Стандартное нормальное распределение записывается: N(0;1); N(m;)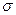

f(х)=;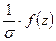

F(X) =;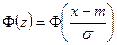

F(z)=;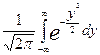

- функция Лапласа (интеграл вероятности Р).

Квантили распределения приводятся в справочной литературе.

F(z)=0,5+=/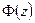

3) Нормальный закон распределения погрешностей:

f(Δ)=.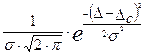

f()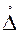

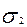
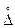
Вероятность попадания 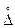в интервале Δ₁; Δ₂ рассчитывается на основании известного свойства функции распределения вероятности:

Р;

.

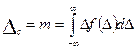Если (Δ_1; Δ₂) расположен симметрично относительно математического ожидания величины Х, т.е. Δ₁= Δ₂=Δ, то вероятность

Р;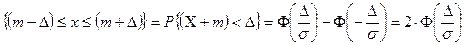

Ф(х)=-Ф(-х).

Закон нормального распределения имеет фундаментальное значение для теории обработки результатов измерений.

Центральная предельная теория утверждает, что закон распределения суммарной погрешности измерений близок к нормальному распределению всякий раз, когда результаты наблюдения формируются под влиянием большого числа независимых случайных составляющих, каждая из которых оказывается лишь случайное действие по сравнению с суммарной погрешностью. Нормальный закон позволяет вести расчеты даже тогда, когда действительный закон не известен, потому что нормальный закон дает чаще увеличенный, чем уменьшенный доверительный интервал.

РАСПРЕДЕЛЕНИЕ

Распределение 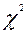, есть распределение непрерывной случайной величины:

х₁, х₂,…, х_n – независимые величины, из которых каждая имеет нормированное нормальное распределение.

N(0;1)

k=n-1 – число степеней свободы (число независимых значений квадратов величин)

f_k(х)= 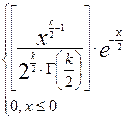,х>0

Г – гамма – функция Эйлера.

Г(р)=.

М;

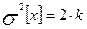
f()

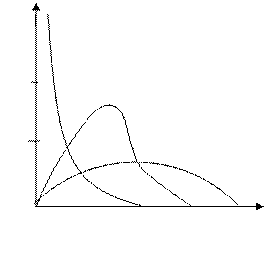
k=2

0,5

k=4

0,25

k=10

6 Х_k

Квантили 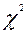- распределения также даны в справочной литературе.

ОСОБЕННОСТИ РАСПРЕДЕЛЕНИЯ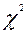

1) Представляет собой частный случай более общего 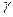- распределения.

2) Величина равная корню квадратному из суммы х² с двумя степенями свободы: - подчиняется распределению Рэлея.

3) Величина равная корню квадратному из суммы 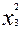, т.е 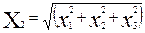подчиняется распределению Максвелла.

4) Распределение 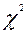при увеличении степеней свободы приближается к нормальному.

РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА.

Распределение непрерывной случайной величины выражается формулой:

t=, где U имеет нормированное нормальное распределение U→N.

х имеет распределение 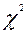; х→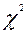

случайные величины U и X являются независимыми.

f (t) = , - ∞ < t < ∞, k = n – 1- число степеней свободы t.

M [ t ]=0, при k =2

, при k =3

Плотность распределения Стьюдента унимодальная, монотонная относительно моды и она симметрична.

Вид плотности распределения Стьюдента

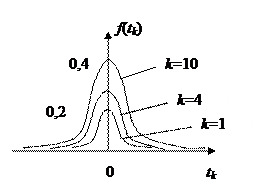При увеличении числа степеней свободы распределение Стьюдента приближается к нормальному распределению.

(закон арксинуса)

Это гармоническое колебание постоянной амплитуды U_max и постоянной частоты можно рассматривать как случайную величину, если начальная фаза есть случайная величина.

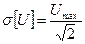
При описании непрерывного распределения используют еще квантили. Квантилем, отвечающим заданному уравнению вероятности P, называется такое значение случайной величины Х_р, при которой функция распределения принимает значение P.

F (Х_р)= P (x < Х_р)= P,

при Р = 0,5 получается квантиль, в этом случае

Р (х < μ_е) = Р (х > μ_е), где μ_е – медиана,

т.е. одинаково вероятно окажется случайная величина меньше или больше медианы. Медиана используется иногда для характеристики центра распределения, а другие квантили для характеристики рассеивания случайной величины.

Если 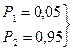, то 5% и 95% квантили ограничивают интервал случайной величины х_0,05 – х_0,95, в котором с вероятностью 0,9 попадают значения случайной величины.

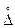
х_0,05 μ_е х_0,95

Для непрерывных случайных величин характеристикой положения является также мода. Мода – это значение случайной величины, при которой плотность распределения f(x), достигает максимума. Если максимумов несколько, то распределение называется полимодальным (двухмодальное, трехмодальное и т.д.). Встречаются распределения, обладающие не максимумом, а минимумом плотности распределения и называются антимодальными.

В теории вероятностей часто приходится сталкиваться с задачами, в которых результат испытаний описывается не одной случайной величиной, а двумя и более, образующими систему. Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных величин ее составляющих, помимо этого они включают взаимные связи (зависимость между случайными величинами). Полной характеристикой системы произвольного числа случайных величин служит закон распределения системы.

Функция распределения системы n случайных величин называется вероятностью совместного выполнения неравенств вида:

n (x₁, x₂, …, x_n)

F (x₁, x₂, …, x_n) = P [(X₁< x₁)(X₂< x₂)…(X_n< x_n)]

Соответственно плотность распределения системы n непрерывных случайных величин называется n -я смешанная частная производная функции распределения, взятая один раз по каждому аргументу.

f (x₁, x₂, …, x_n) =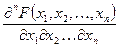

Второй смешанный центральный момент называется попарным корреляционным моментом системы случайных величин.

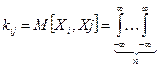(x_i – m_i)(x_j – m_j) f (x₁, x₂, …, x_n) dx₁dx₂...dx_n

Корреляционный момент описывает помимо рассеивания случайных величин еще и связь между ними. Если k_ij ≠ 0, то это признак наличия зависимости между величинам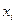и и 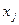системы случайных величин.

На практике удобно пользоваться коэффициентом корреляции:

r_ij характеризует степень линейной зависимости случайных величин. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (убывать) по линейному закону. Эта тенденция к линейной зависимости может быть более или менее ярко выраженной.

r_ij характеризует степень тесноты линейной зависимости между случайными величинам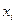и и 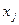и может принимать значения - 1 ≤ r_ij < 1.

Для независимых случайных величин r_ij = 0 (обратное утверждение не всегда справедливо).

Рассмотрим распределение плотности вероятности суммы нескольких независимых случайных величин, что очень существенно для определения закона распределения общей погрешности измерений, если она складывается из небольшого числа составляющих.

Полная погрешность Δ = Δ₁ + Δ₂, причем составляющие имеют плотность распределения вероятности f ₁(Δ₁) и f ₂(Δ₂), плотность распределения вероятности суммы двух независимых случайных погрешностей можно записать:

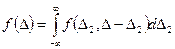
Плотность распределения суммы Δ₁ и Δ₂ с нормальными законами распределения можно записать следующим образом:

,

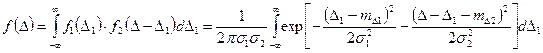где 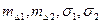- математические ожидания и среднеквадратические отклонения погрешностей Δ₁ и Δ₂.

В результате интегрирования получается:

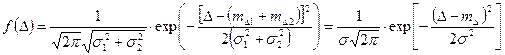
Отсюда следует, что закон распределения суммы двух независимых случайных величин распределяемый по нормальному закону также является нормальным.

Функции распределения узаконены стандартом ГОСТ 8.011-72.

При бесконечном числе испытаний случайная величина может принимать любые значения, называемые генеральной совокупностью, а некоторое число n этих значений называется выборкой объем n. Определяя по этим значениям выборки характеристики закона распределения, получаем не истинные значения дисперсии и среднеквадратического отклонения, характерные для всей генеральной совокупности, а только их оценки (выборочные величины), также случайно отклоняющиеся от истинного значения.

Если истинное значение искомой величины равно 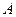, то ее оценка . Последняя является функцией, зависящей от от вида распределения случайной величины и самих результатов измерения.

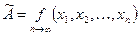
Вид таких функций должен удовлетворять некоторым условиям, при которых имеет смысл принимать за наилучшее приближенное значение искомой величины 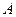ее оценку.

Способы нахождения статистических оценок для конечного ряда наблюдений и показателя их качества зависят от законов распределения.

К оценкам случайной величины, получаемым по статистическим данным, предъявляются требования:

- состоятельности;

- несмещенности;

- эффективности.

Состоятельной считается оценка параметра 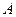, если при увеличении числа наблюдений n она стремится (сходится по вероятности) к истинному значению оцениваемой величины, т.е. при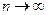

Несмещенной является оценка, математическое ожидание которой равно истинному значению оцениваемой величины.

Эффективной будет та оценка из нескольких возможных несмещенных, для которой оценка дисперсии будет минимальной.

В качестве оценки истинного значения принимается среднее арифметическое полученных результатов измерения:

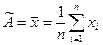
Математическое ожидание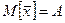

Несмещенными будут и другие оценки, являющиеся линейной функцией результатов наблюдения.

Среди всех рассмотренных оценок только среднее арифметическое имеет наименьшую дисперсию.

Дисперсия среднего арифметического в n раз меньше дисперсии единичного наблюдения.

Более полным и надежным способом оценки случайной величины является определение интервальной оценки (а не единичного точечного измерения), которая с заданной степенью достоверности включает в себя значение оцениваемого параметра.

При интервальной оценке определяется доверительный интервал (Δ₁;Δ₂), между границами которого с определенной доверительной вероятностью Р находится истинное значение

Доверительная вероятность определяет область допустимых значений, а уровень значимости - критическую область.

Выбираемое значение q должно быть достаточно малым, чтобы не была совершена ошибка первого рода, т.е. чтобы не была забракована правильная оценка. С другой стороны слишком малое значение q может привести к ошибке второго рода, т.е. когда будет принята ложная оценка.

0,02 ≤ q ≤ 0,1

В общем случае доверительный интервал можно строить на основе неравенства Чебышева, при этом необходимо знать не вид распределения наблюдений, а среднеквадратическое отклонение σ_x случайной величины. С помощью σ_x можно оценить вероятность того, что при однократном наблюдении случайная погрешность по абсолютному значению не превысит некоторого наперед заданного значения ε, т.е. вероятность Р {|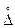| < ε } ≥ .

Однако полученные с помощью неравенства Чебышева интервалы оказываются слишком широкими, поэтому на практике выясняют вид распределения выборочных характеристик, используемых в качестве оценки выборочной величины, и задаются доверительной вероятностью и далее определяют доверительный интервал.

Оценка грубых наблюдений.

При обработке результатов наблюдений случайной величины заведомо подчиняющихся нормальному закону распределения при принятии решения об исключении или сохранении резко отклоняющихся результатов (грубых промахов) нужно быть очень осторожным и анализировать условия, в которых получается результат. Сомнительным может быть лишь наибольшее или наименьшее из результатов наблюдения. Вопрос о том, содержит ли данный результат грубую погрешность, решается общими методами статистических гипотез.

Дата добавления: 2014-01-20