Методы обработки результатов прямых измерений

Прямые измерения – это измерения, в результате которых находят непосредственно искомое значение величин.

При однократных измерениях точность результатов оценивают по нормируемым метрологическим характеристикам (МХ) применяемых СИ. Погрешность результата однократного измерения оцениваются на основании априорной информации или либо суммарной погрешности СИ, класса точности СИ или составляющих: инструментальной и методической погрешностей.

1. Если известен класс точности СИ, то согласно ГОСТ 8.407 – 80 можно определить допустимые пределы погрешности СИ Δ_д = Δ_и. По значениям, полученным с помощью СИ x_си и допустимым пределам погрешности СИ можно определить пределы погрешности данного однократного измерения.

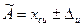
2. Если кроме пределов инструментальной и систематической погрешностей известны допустимые пределы методической погрешности, то в этом случае суммарная погрешность определяется алгебраической суммой

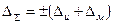
3. Если известны пределы других, не исключенных систематических погрешностей, то при оценке их границ в соответствии с ГОСТ 8.207 – 76 данная погрешность рассматривается как СВ, распределение равномерно и симметрично в пределах 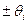. Тогда суммарная погрешность определяется по формуле:

,

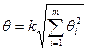где k – коэффициент, определяемый принятой доверительной вероятностью Р

(при доверительной вероятности равной 0,95 k = 1,1), θ_i – границы i -й неисключен-

ной составляющей погрешности.

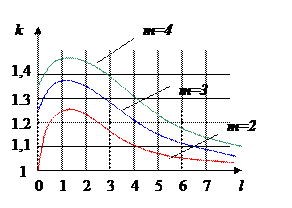
Если число m неисключенной СП больше 4, то k выбирают из ряда:

P	0,9	0,95	0,98	0,99
k	0,95	1,1	1,3	1,4

Если m ≤ 4, k определяют по графику зависимости k (m,l) (см. рис.).

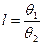выражает отношение границы наибольшей составляющей неисключенной

СП (НСП) к ближайшей к ней по значению границы из остальных составляющих.

4. Если известны СКО случайных составляющих погрешности, распределенных по нормальному закону, СКО и доверительные границы случайной составляющей суммарной погрешности результата однократного измерения, то суммарное значение находится:

,

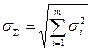
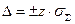где z – коэффициент нормального распределения соответствующей заданной до –

верительной вероятности, берется из таблиц Лапласа.

5. Если распределения погрешности отличны от нормальных, то определяют их композицию и коэффициент z для заданной доверительной вероятности, а суммарная погрешность результата однократного измерения при известных оценках систематической случайной составляющей рекомендуется оценивать по ГОСТ 8.207 – 76.

6. Если погрешность при однократном наблюдении оказывается выше допустимой, то выбирают более точные СИ или применяют прямые измерения с многократными наблюдениями.

Дата добавления: 2014-01-20