
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямые равноточные измерения с многократными наблюдениями
|
|
|
|
Результаты многократных наблюдений, полученных при прямых измерениях величины А называются равноточными (равнорассеянными), если они являются независимыми и одинаково распределенными случайными величинами. Сами измерения проводятся одним наблюдателем в одинаковых условиях внешней среды с помощью одного и того же СИ.
Статистическая обработка группы результатов наблюдения при равноточных измерениях в нормальном распределении этих результатов выполняется в такой же последовательности, как рекомендует ГОСТ 8.207 – 76 и включает следующие этапы:
1) исключаются известные СП из результатов измерения;
2) вычисляются средние арифметические исправленных результатов наблюдения, принимаемых за результат измерения.
3) Вычисляется случайное отклонение υi результата отдельных наблюдений от среднего арифметического исправленных результатов (как по числовому значению, так и по знаку);
4) Вычисляется оценка СКО результата наблюдения;
5) Проверяется гипотеза о том, что результат наблюдения принадлежит нормальному распределению;
6) Вычисляется оценка СКО результата измерения, доверительные границы случайной погрешности ε, неисключенных остатков СП θ и погрешности результатов измерения Δ.
Среднее арифметическое исправленных результатов измерения:
 ,
,
где xi – i-й результат наблюдения.
Случайное отклонение 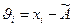 всех результатов отдельных наблюдений от среднего арифметического исправленного результата наблюдения принимается за остаточные погрешности, обладающие следующими свойствами:
всех результатов отдельных наблюдений от среднего арифметического исправленного результата наблюдения принимается за остаточные погрешности, обладающие следующими свойствами:
1) сумма остаточных погрешностей равна нулю, т.е.

2) сумма квадратов остаточных погрешностей минимальна, т.е.
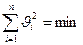
Эти свойства используются при обработке результатов измерения для контроля качества измерения.
Свойство 2 вытекает из принципа Лежандра, положенного в основу метода наименьших квадратов.
Оценка СКО результата наблюдений вычисляется по приближенной формуле Бесселя:
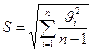
Эта оценка является несмещенной, состоятельной и эффективной. Деление суммы  на (n – 1) вместо n приближает вычисленное значение S к его теоретическому значению и чем больше n, тем это приближение лучше.
на (n – 1) вместо n приближает вычисленное значение S к его теоретическому значению и чем больше n, тем это приближение лучше.
Оценка СКО характеризует степень рассеяния результата измерения вокруг среднего арифметического значения и определяется совокупностью условий измерения (свойствами прибора, качествами экспериментатора, факторами, влияющими на измерение).
Гипотеза о том, что результат измерения принадлежит нормальному распределению определяется по уравнению значимости  %.
%.
1) При большом числе наблюдений (n > 50) гипотезы проверяются по критерию Пирсена (χ2), Колмогорова, Мизеса – Смирнова (ω2).
2) При n > 3, n ≤ 50 по специальному критерию W для нормального или логарифмического нормального распределения. Если результаты наблюдения можно считать, что они принадлежат нормальному распределению, то из результатов наблюдения исключаются грубые погрешности, а т.к. среднее арифметическое обладает некоторой случайной погрешностью, то вводится понятие оценки СКО среднего арифметического. Его выражают следующим образом:
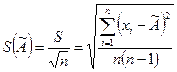
Оценка среднего арифметического 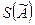 несмещенная, состоятельная, эффектив –
несмещенная, состоятельная, эффектив –
ная.
Доверительные границы ε случайной погрешности результата измерения без учета знака находят по формуле:
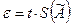
где t – коэффициент Стьюдента, который зависит от заданной доверительной вероятности Р и числа результатов наблюдения.
Доверительные границы неисключенной систематической погрешности результатов измерения вычисляют путем построения композиции распределения, составляющей неисключенной систематической погрешности при равномерном распределении всех составляющих, эти границы (без учета знака) можно вычислять по формуле:
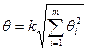
где k – коэффициент, определяемый принятой доверительной вероятностью, m – число суммируемых неисключенных погрешностей.
k задан таблично либо в виде графика:

Доверительная вероятность Р принимается такой же, что и при вычислении доверительных границ случайной погрешности результата измерения.
Доверительные границы погрешности Δ результата измерения зависят от отношения

где 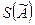 - отклонение от среднего арифметического.
- отклонение от среднего арифметического.
Если Δ < 0,8, то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают Δ = ε.
Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения, не превышает 15% при выполнении указанных неравенств.
Если Δ > 0,8, то систематической погрешностью по сравнению с систематической пренебрегают и Δ = θ.
В случае, если неравенства не выполняются, границу погрешности результата измерения находят путем построения композиции распределения случайных погрешностей и неисключенных систематических погрешностей, рассматриваемых как случайные величины.
Границы погрешностей результата измерения Δ без учета знака вычисляются по формулам:


В данном случае k – это коэффициент, зависящий от соотношения случайных и неисключенных систематических погрешностей.

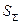 - оценка суммарного СКО результата измерения.
- оценка суммарного СКО результата измерения.
При симметричной доверительной погрешности результат измерения представляется в форме  ; Δ; Р.
; Δ; Р.
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности Δ.
При отсутствии данных о виде функции распределения составляющих погрешности и необходимости дальнейшей обработки результатов, форма записи следующая:
 ;
; 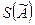 ; n; θ,
; n; θ,
где n – объем выборки.
В случае, если границы неисключенной СП вычислены по формуле 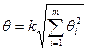 , то следует дополнительно указывать доверительную вероятность Р:
, то следует дополнительно указывать доверительную вероятность Р: 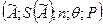 .
.
При окончательной записи результата измерения требуется выполнить округление результата измерения. При расчетах следует найти погрешность
Получен. Оценки и оставить в результате только первые (одну, две) значащих цифры. Если полученное число начинается с цифры 1 или 2, то отбрасывание второго десятичного знака приводит к ошибке до 30-50 %, что недопустимо. А если полученное число начинается с цифры 9, то сохранение второго знака является дезинформацией, так как исходные данные не обеспечивают такой точности (достоверности).
Существуют следующие правила округления:
1) Если полученное число начинается с цифры 1 или 2, то сохраняется два знака.
2) Если с цифры 3 и более, то сохраняется лишь один знак.
В соответствии с этим правилом установлены нормируемые значения погрешности средств измерений.
Правила округления:
1) Любой результат расчета или измерения округляется в соответствии с его погрешностью, поэтому одновременно с округлением результата должна оцениваться его погрешность.
2) Погрешность результата измерения указывается двумя значащими цифрами, если первая из них 1 или 2, и одной, если 3 и более.
3) Округления производятся лишь в окончательном ответе, а все предварительные расчеты выполняются не менее чем с 1-2 лишними знаками.
Правила проверки согласия опытного распределения случайной величины с теоретическим распределением.
Для проверки опытного распределения с теоретическим случайной величины x формулируют проверочную гипотезу, то есть:
1) Выбирают теоретическое распределение случайной величины, согласие которого с опытным распределением этой величины следует проверять.
2) Дополнительно выбирают целесообразный критерий.
3) Задают уровень значимости, при котором требуется провести проверку. Для задания уровня значимости устанавливают соответствующую одностороннюю критическую область критерия согласия, либо двусторонние области.
При помощи результатов наблюдений определяют опытное распределение, оценки неизвестных параметров выбранного теоретического распределения и соответствующее значение критерия проверки. Проверяемая гипотеза отвергается, если вычисленное значение критерия проверки попадает в критическую область. В противном случае гипотеза принимается.
Один из критериев – это критерий Пирсена (χ2) для большого объема выборки (n>50). По экспериментально полученным значениям случайной величины x, даже при n→∞ наблюдений, построить плавные кривые функции распределения F(x) или плотности распределения f(x) не представляется возможным, поэтому на основании экспериментальных данных строится гистограмма fi*(x) статического распределения в виде столбцов.
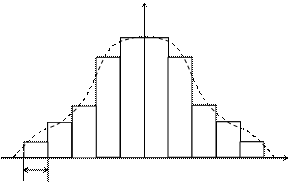 fi*(x)
fi*(x)
x
Δxi
Полученные значения xi располагаются в порядке возрастания. Затем все результаты наблюдений делят на r малых интервалов длиной Δxi (i = 1,2, …, r) (при n = 30-100 рекомендуется выбирать r=5-9). Подсчитывают частоты mi*, равные числу результатов наблюдения, лежащих в каждом i–ом интервале и оценки средней плотности распределения в интервале Δxi.

По оси абсцисс откладывают в определённом масштабе интервалы Δxi в порядке их возрастания, и на каждом строят прямоугольник высотой, равной оценке средней плотности распределения. Площадь всех прямоугольников равна 1. После построения гистограммы теоретически подбирают плавную кривую распределения fi*(x), которая отражает все основные черты статистического распределения.
Суть критерия χ2 состоит в контроле отклонений гистограммы опытных данных, от гистограммы с таким же числом интервалов, построенной на основе теоретического нормального распределения f(x). Сумма квадратов разности опытной частоты mi* и теоретической mi не должна превышать значений χ2k,q, в зависимости от заданного уровня значимости q и числа степеней свободы k=r-3. 3 – число наложенных связей.
1) Вместо бесконечного числа измерений принимается конечное число n.
2) Вместо среднеквадратического отклонения σ принимается оценка S.
3) Вместо истинного значения измеряемой величины x принимается среднее арифметическое Ã.
По уровню значимости q и числу степеней свободы k можно определить границы одностороннего критерия области χ2k,q из таблиц. Для найденного значения χ2k,q:

Для найденного значения χ2 справедливо условие


То есть вероятность того, что вычисленное значение χ2 превысит χ2k,q равна q, и критическую область образуют все значения χ2 >χ2k,q.
Критерий 2.
Можно считать, что результаты наблюдений принадлежат распределению, если не больше m разностей |xi-Ã| превысили значение Zp/2S, где Zp/2 – верхний квантиль распределения нормированной функции Лапласа, отвечающей вероятности р/2.
 - оценка среднеквадратического отклонения результата наблюдений.
- оценка среднеквадратического отклонения результата наблюдений.
Значение вероятности р можно определить по выбранному уровню значимости q/2 и числу результатов наблюдений n. В случае если при проверке нормальности распределение результатов наблюдений группы для критерия 1, уровень значимости равен q1, а для критерия 2 уровень значимости q2, то результирующий уровень значимости 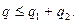 В случае, если хотя бы один из критериев не соблюден, то считают, что распределение результатов наблюдений группы не соответствует нормальному. При числе результатов
В случае, если хотя бы один из критериев не соблюден, то считают, что распределение результатов наблюдений группы не соответствует нормальному. При числе результатов  принадлежность их к нормальному распределению не проверяется. А если заранее известно, что распределение нормальное, то обработка проводится по данной методике.
принадлежность их к нормальному распределению не проверяется. А если заранее известно, что распределение нормальное, то обработка проводится по данной методике.
Прямые неравноточные.
В практике измерения имеют место неравноточные измерения, когда измерения одной и той же измеряемой величины проводятся разными наблюдателями с применением разнообразных средств, методов и условий среды. Оценки их дисперсий значительно отличаются друг от друга, а средние арифметические являются оценками одного и того же значения измеряемой величины. За основу расчета принимается:
1) Среднее арифметическое m рядов равноточных результатов наблюдений измеряемой величины, то есть Ã1, Ã2, …, Ãm.
2) Оценки среднеквадратического отклонения результатов измерений в отдельных рядах: S(Ã1), S(Ã2), …, S(Ãm).
3) Число наблюдений в каждом ряду: n1, n2,…, nm.
Наиболее достоверным значением измеряемой величины является средневзвешенное значение Ã0, связанное с исходными средними арифметическими Ãj (j=1,…, m) и их весовыми коэффициентами Qi следующим соотношением:

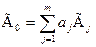 , где аj – коэффициент, характеризующий степень доверия к оценке Ãj.
, где аj – коэффициент, характеризующий степень доверия к оценке Ãj.
Для математического ожидания справедливо равенство:

Так как систематическую погрешность в данном случае исключает сумма всех коэффициентов:  .
.
Весовые коэффициенты определяются из условия обращения в минимум дисперсии средневзвешенного и условия:
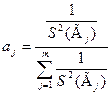 .
.
Значение самой дисперсии средневзвешенного определяется по формуле:
 .
.
Если теоретические дисперсии неизвестны, то используются их оценки S2(Ãj), а для определения доверительных границ погрешности результатов измерения при  используют нормированное нормальное распределение. Тогда погрешность определяется:
используют нормированное нормальное распределение. Тогда погрешность определяется:
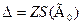 .
.
При малом числе nj используют распределение Стьюдента с числом степеней свободы k=n-1:
 ,
,  .
.
Косвенные измерения.
Измеряемая величина А является функцией от каких-либо значений:
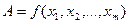 .
.
Для простоты считают, что значения xi распределены по нормальному закону, измерения равноточные, погрешности измерения не коррелированны между собой. Очевидно, что абсолютная погрешность Δ измеряемой величины А является также функцией погрешности прямых измерений.
 ,
,  ,
,
если А зависит от одного значения. Затем данную функцию разлагают в ряд Тейлора и ограничиваются первыми членами ряда:
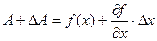 ,
, 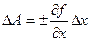 ,
, 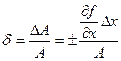 .
.
Разложением в ряд Тейлора до какого-то члена определяют точность. Когда 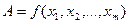 , абсолютную погрешность можно записать:
, абсолютную погрешность можно записать:
 .
.
Если результаты прямых измерений xi определены с каким-то среднеквадратическим отклонением Si, то оценка среднеквадратического отклонения результатов косвенных измерений будет выражаться:
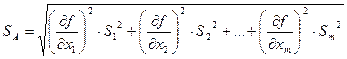 .
.
Если погрешности измерений x1, x2, …, xm коррелированны, то оценка среднеквадратического отклонения выглядит следующим образом:
 .
.
ri,j – коэффициент корреляции  ).
).
Установление корреляционных связей между погрешностями в большинстве случаев затруднительно, поэтому, если эти связи есть, то ri,j = 1, если они отсутствуют или очень малы ri,j = 0.
Величина  - частная погрешность косвенного измерения. Не все частные погрешности косвенных измерений играют равную роль в формировании итоговой погрешнсти результатов измерений. Отдельные составляющие могут не оказывать никакого влияния на суммарную погрешность. Поэтому, если в равенстве
- частная погрешность косвенного измерения. Не все частные погрешности косвенных измерений играют равную роль в формировании итоговой погрешнсти результатов измерений. Отдельные составляющие могут не оказывать никакого влияния на суммарную погрешность. Поэтому, если в равенстве  k-тая частная погрешность меньше суммарной погрешности, то ей можно пренебречь. Это условие называется критерием ничтожных погрешностей, а сами погрешности, удовлетворяющие этому критерию, ничтожными.
k-тая частная погрешность меньше суммарной погрешности, то ей можно пренебречь. Это условие называется критерием ничтожных погрешностей, а сами погрешности, удовлетворяющие этому критерию, ничтожными.
Использование этого критерия позволяет выявить те величины, повышение точности измерений которых уменьшает суммарную погрешность результата, и те величины, точность которых не следует повышать и которые можно не учитывать.
При интервальной оценке случайной погрешности результатов косвенного измерения определяют доверительные границы с помощью коэффициента Стьюдента, а затем и оценки истинного значения.
Количественные показатели точности измерения и способы их выражения.
Показателями точности измерений являются:
1) Интервал, в котором погрешность измерения находится с заданной вероятностью.
2) Интервал, в котором систематическая составляющая погрешности находится с заданной вероятностью.
3) Числовые характеристики систематической и случайной составляющих погрешности измерения.
4) Функция распределения (плотность вероятности) систематической и случайной составляющих погрешности измерения.
Точность измерения должна выражаться одним из следующих способов:
1) Интервалом, в котором с установленной вероятностью находится суммарная погрешность измерения.
2) Интервалом, в котором с установленной вероятностью находится систематическая погрешность измерений.
3) Стандартной аппроксимацией функции распределения (плотности вероятности) случайной составляющей погрешности измерения и среднеквадратического отклонения случайной погрешности измерения.
4) Стандартными аппроксимациями функций распределения систематической и случайной составляющих погрешности измерения и их среднеквадратических отклонений.
5) Функциями распределения систематической и случайной составляющих погрешности измерения.
Выбор способа определяется назначением измерений и характером их использования. Формы представления результатов измерения определены ГОСТ 1317-86.
1) Результаты измерений представляются именованным или неименованным числом.
2) Совместно с результатами измерений должны быть представлены характеристики их погрешностей или их статистические оценки.
Характеристиками погрешности измерений являются:
1) Среднеквадратические отклонения погрешностей.
2) Границы, в которых она находится с заданной вероятностью (верхняя и нижняя границы заданного интервала вероятности).
3) Характеристики случайной составляющей погрешности (среднеквадратическое отклонение, нормированная автокорреляционная функция).
4) Характеристики неисключенной систематической составляющей погрешности (среднеквадратического, границы, в которых неисключенная систематическая находится с заданной вероятностью).
Указываются нормы (пределы допускаемых значений) и приписные значения (наибольшие и наименьшие).
Статистическими оценками являются оценки и границы доверительного интервала характеристик погрешностей. Вместо характеристик погрешностей допускается указывать аттестованную методику, удовлетворяющую данным характеристикам погрешностей.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1009; Нарушение авторских прав?; Мы поможем в написании вашей работы!