Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому

Силы в зацеплении прямозубой конической передаче

Согласно схеме разложения сил на рисунке, приведенном выше, в зацеплении действуют три силы: окружная Ft, радиальная Fr и осевая Fa. Сила Fn действует по нормали к зубу. Для шестерни формулы запишутся:

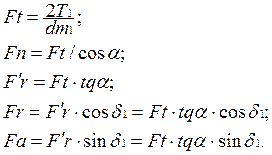
Для колеса направление сил противоположное.

Параметры эквивалентных колес необходимы при расчетах на прочность. Форма зуба конического колеса в нормальном сечении дополнительным конусом с углом φ₁ такая же, как у цилиндрического прямозубого колеса. Эквивалентное цилиндрическое колесо получают как развертку дополнительного конуса, которая ограничена углом φ₂. Диаметры эквивалентных колес:

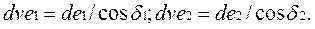
Запишем через модуль и число зубьев:

Для числа зубьев эквивалентных колес:

Таким образом, изучение пары конических колес с числом зубьев z₁ и z₂ и модулем m_e можно заменить парой цилиндрических колес с числом зубьев zv₁ и zv₂ с тем же модулем.

Расчет зубьев прямозубой конической передачи по напряжениям изгиба

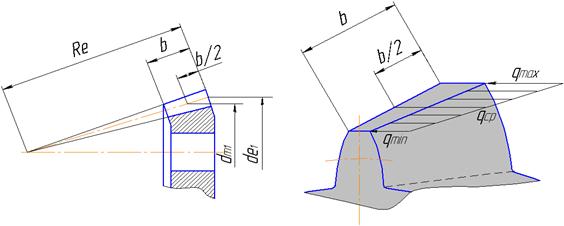
Размеры поперечных сечений зуба конического колеса изменяются пропорционально расстоянию этих сечений от вершины конуса. Все поперечные сечения зуба геометрически подобны. При

этом удельная нагрузка распределяется неравномерно по длине зуба. Так как модуль зубьев и нагрузка изменяются одинаково, то напряжения изгиба остаются постоянными по всей длине зуба. Это позволяет вести расчет по любому из сечений. Обычно за расчетное сечение принимают среднее сечение зуба с нагрузкой q_m=q_cp (см. рис.)

По аналогии с прямозубой цилиндрической передачей запишем:

,

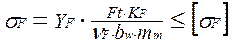где ν_F = 0,85 - опытный коэффициент, характеризующий понижение прочности конической прямозубой передачи по сравнению с цилиндрической; m_m – модуль в среднем нормальном сечении зуба; Y_F – коэффициент формы зуба, который определяют по графику в соответствии с эквивалентным числом зубьев z_ν.

K_F – коэффициент расчетной нагрузки, причем также

K_F = k_Fβ k_Fν.

Дата добавления: 2014-01-20