Степень подвижности механизма

Кинематические цепи и кинематическая схема механизма

Классификация кинематических пар

Ведущие и ведомые звенья

Ведущим звеном механизма называют одно звено, для которого элементарна работа вешних сил, приложенных к нему, является положительной.

Ведомым звеном называется звено, для которого элементарная работа внешних сил, приложенных к нему, является отрицательной или равна нулю.

Подвижное соединение двух соприкасающихся звеньев, допускающее их относительное движение называется кинематической парой.

Все кинематические пары подразделяются по числу степеней свободы на одно-, двух-, трех-, четырех -, пятиподвижные.

Таблица №1

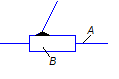
Число степеней свободы	Класс пары	Название	Рисунок	Условное изображение
		Поступательная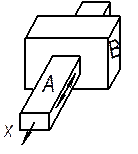
		Вращательная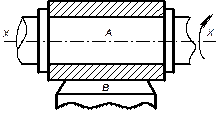
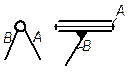
		Цилиндрическая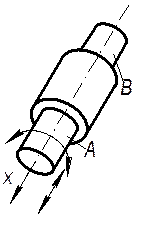
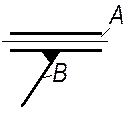
		Сферическая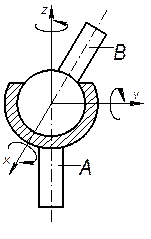
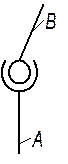
		Цилиндр-плоскость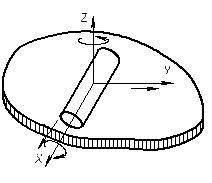
		Шар-плоскость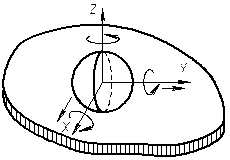

Возможное движение звеньев кинематических пар при определении степени подвижности должна быть независимыми. Так винтовая кинематическая пара (Рис. 1.2) допускает 2-а движения – вращательное и поступательное, однако эти движения зависимы друг от друга (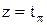; где t- шаг винта), поэтому эту кинематическую пару нужно рассматривать как одноподвижную.

Кинематические пары делятся на низшие и высшие.

Кинематическая пара, которая образована звеньями, соприкасающимися по поверхности, называется низшей кинематической парой.

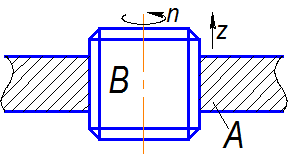
Рис. 1.2

Кинематическая пара, которая образована звеньями, соприкасающимися только по линии или в точке, называется высшей кинематической парой.

Кинематической цепью называется связанная система звеньев, образующих между собой кинематические пары.

Кинематические цепи делятся на простые и сложные.

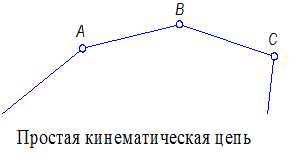
Простой кинематической цепью называется такая цепь, у которой каждое звено входит не более чем в две кинематические пары.

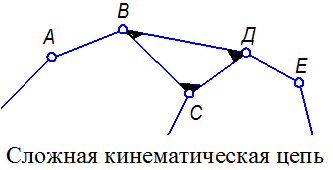
Сложной кинематической цепью называется цепь, в которой имеется хотя бы одно звено входящее более чем в две кинематические пары.

Рис. 1.3

Простые и сложные кинематические цепи делятся на замкнутые и незамкнутые.

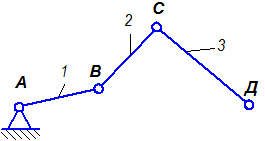
Замкнутой кинематической цепью называется цепь, каждое подвижное звено которой входит, по крайней мере, в две кинематические пары (Рис. 1.4а).

Незамкнутой кинематической цепью называется цепь, в которой есть звенья, входящие только в одну кинематическую пару (Рис. 1.4б).

а) Замкнутая	б) Незамкнутая
Рис. 1.4

Кинематической схемой механизма называется его изображение в выбранном масштабе с применением условных обозначений, установленных ГОСТом, звеньев и кинематических пар.

Схема позволяет определить движение ведомых звеньев по заданному движению ведущих.

АВ – ведущее звено, т.е звено движение которого задано.

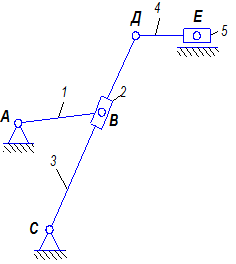
Рис. 1.5

Обобщенной координатой механической системы (механизма) называется независимая координата, однозначно определяющая положение системы в пространстве.

Число обобщенных координат определяет число степеней свободы системы.

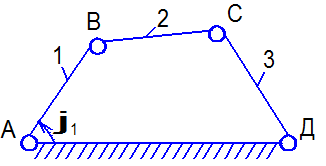
Рис. 1.6

Свободное твердое тело (звено) в пространстве обладает 6 степенями свободы, т.е. оно может совершать 3 независимых поступательных движения вдоль взаимно-перпендикулярных осей и 3 вращательных движения вокруг тех же осей.

Если же звено входит в кинематическую пару, то на относительное движение его, т.е. на движение по отношению ко второму звену, входящему в эту пару накладываются определенные ограничения. Эти ограничения называются условиями связи - S.

По числу условий связи, накладываемых на относительные движения звеньев, пары подразделяются на классы.

Класс кинематической пары соответствует числу условий связи, накладываемых на относительное движение звеньев, входящих в эту пару.

В зависимости от способа соединения звеньев в кинематическую пару число условий связи может меняться от 1 до 5.

Поэтому все кинематические пары можно разделить на 5 классов.

К I классу относятся пары, накладывающие на относительное движение звеньев одно условие (5-ти подвижные пары).

Ко II классу относятся пары, накладывающие два условия (4-х подвижные) и т.д.

Если на движение звена в пространстве, не наложено ни каких условий связи, то оно обладает 6 степенями свободы.

Тогда, если число звеньев кинетической цепи - К, то общее число степеней свободы, которым обладают К звеньев до их соединения в кинетическую цепь - 6 К

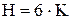(степень свободы) до соединения в кинематическую цепь.

Соединение звеньев в кинематическую цепь накладывает различное число связей на относительное движение звеньев, зависящее от класса пар. Если число пар I класса обозначить P₁, II класса – P₂, III класса – P₃, IV класса – P₄, V класса – P₅,

то из 6к степеней свободы, которыми обладали звенья до их вхождения в кинематические пары, необходимо исключить те степени свободы, которые отнимаются вхождением звеньев в кинематические пары.

Тогда число степеней свободы Н, которым обладает кинематическая цепь будет равно:

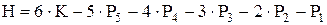
(1.1)

Если одно из звеньев кинематической цепи будет неподвижным, то общее число степеней свободы цепи уменьшится на 6 и число степеней свободы W относительно неподвижного звена будет равно:

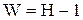
(1.2)

Число W степеней свободы кинематической цепи относительно стойки называется числом степеней неподвижности (степенью неподвижности) кинематической цепи.

Подставляя (1.1) во (1.2):

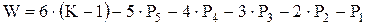
если обозначить (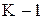) через n то получим:

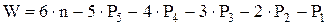
где n - число подвижных звеньев кинематической цепи.

Это равенство носит название формулы подвижности или формула Сомова-Малышева.

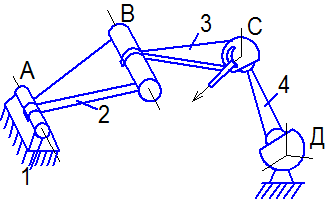
а) кинематическая цепь

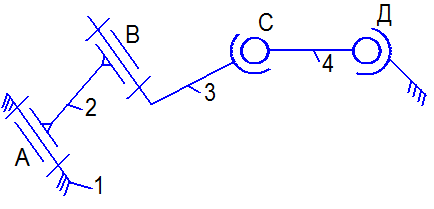
б) схема кинематической цепи

Рис. 1. 7

Звенья 1 и 2 - входят в к.пару A (V кл.)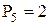
2 и 3 - в пару В (V кл.)
3 и 4 - в пару С (IV кл.)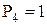
4 и 5 - в пару D (III кл.)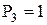

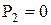
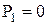
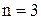
Подставим в формулу и получим

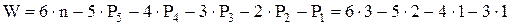
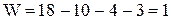
Степень свободы (подвижности) механизма показывает, сколько надо задать независимых координат, чтобы характеризовать положение любого звена механизма относительно стойки.

Если механизм обладает 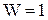, то при заданном движении одного из звеньев (ведущего) все остальные звенья будут иметь вполне определенные движения.

Если 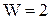, то определенность движения звеньев может быть обеспечена или двумя ведущими звеньями имеющим по одному независимому движению, или одним ведущим звеном, имеющим 2 независимых движения (двухподвижных).

Выделим формулу для определения числа степеней свободы плоского механизма, звенья которого совершают движения параллельно одной какой-либо плоскости.

В этом случаи из 6 движений, которое каждое отдельное звено может совершать в пространстве, исключаются 3 движения - одно поступательное и два вращательных.

Следовательно, звено в плоскости может совершать только 3 движения.

При этом условии в состав плоских кинематических цепей могут входить лишь кинематические пары 4 и 5-го классов, т.е. кинематическая пара 5 кл. лишает 2-х из 3-х оставшихся движений, а кинематическая пара 4 кл. - 1 простейшего движения.

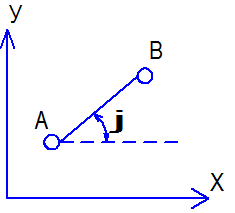
Рис. 1.8

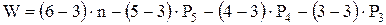
то степень подвижности плоского механизма:

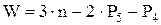- структурная формула плоского механизма или формула Чебышева.

В состав плоских механизмов пары 1,2 и 3 кл. входить не могут. Кинематические пары 5 к. входящие в состав плоского механизма могут быть в 2-х видах:- либо в виде вращательной пары либо в виде поступательной пары. (т.е. низшие).

Кинематические пары 4 кл. - являются высшими кинематическими парами имеющими 2 степени свободы.

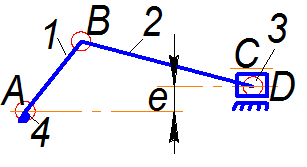
Рис. 1.9

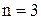
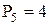
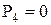
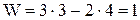
Дата добавления: 2014-01-20