Передаточное отношение планетарных и дифференциальных механизмов

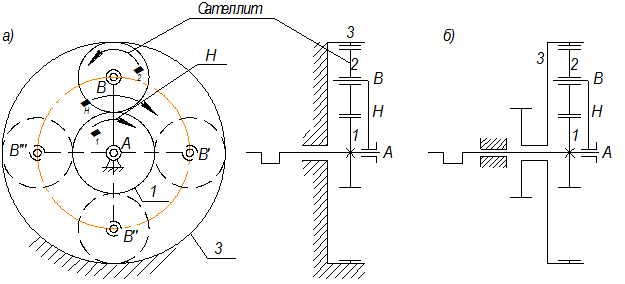
(рис. 2.14)

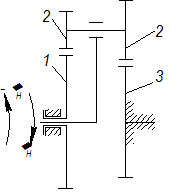
Звенья, вращающиеся вокруг неподвижной оси, называются основными или центральными.

Центральное колесо 1 называется солнечным, а неподвижное 3 - коронным или корончатым. Зубчатое колесо 2 имеющее подвижную ось называется сателлитом. Звено Н называется водилом или поводком. Механизмы, в состав которых входят зубчатые колеса с подвижными осями называются планетарными или дифференциальными.

Планетарными (рис. 2.14 а) называются механизмы, имеющие одну степень свободы. Дифференциальные (рис. 2.14 б) механизмы имеют две и более степени свободы.

Рис. 2.14

Эти механизмы обязательно должны быть соосными, то есть оси солнечных колёс должны располагаться на одной и той же прямой линии.

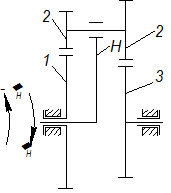
Рассмотрим дифференциальный механизм (рис. 2.15).

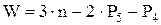
где: n=4; ; .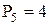

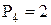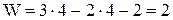, таким образом определённость в движении звеньев этого механизма будет в том случае, если будут известны законы движения двух его ведущих звеньев.

Так как сателлиты имеют подвижные оси, то использовать формулы для расчёта передаточного отношения механизмов с неподвижными осями не представляется возможным. В этом случае прибегают к методу инверсии (метод обращённого движения).

Будем рассматривать движение всех колёс относительно водила. Всем звеньям зададим вращательное движение с угловой скоростью водила, но в обратном направлении и найдём скорости всех звеньев механизма. Для этого вычтем угловую скорость водила из всех угловых скоростей колёс.

Рис. 2.15

Таблица 2.

№ Звеньев	Скорость звена в действительном движении (до инверсии)	Скорость звена в обращённом движении (после инверсии)
Колесо 1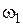
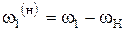
Колесо 2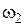
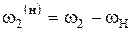
Колесо 2’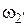
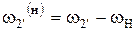
Колесо 3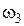
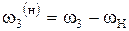
Звено Н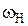

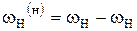
Механизм, полученный в результате инверсии (остановки водила) называется обращённым (рис. 2.16). В результате получили обычную зубчатую передачу с неподвижными осями.

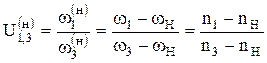
(2.1)

Эту зависимость (2.1) называют формулой Виллиса для дифференциальных механизмов.

Если бы было n - колёс, то:

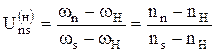
где s – солнечное колесо.

Дифференциальный механизм никакого определённого передаточного отношения не имеет, если ведущим является одно из звеньев (колесо или водило), и приобретает определённость, если ведущих колёс будет два.

Рис. 2.16

Передаточное отношение 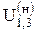обращённого механизма можно рассчитать,

зная числа зубьев колёс.

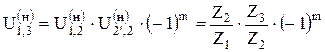
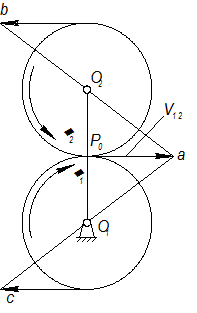
У планетарных механизмов (рис. 2.16) одно из центральных (основных) колёс неподвижно, тогда формула Виллиса примет вид:

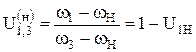
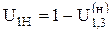
или в общем случае: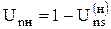

Рис. 2.17

Передаточное отношение планетарного механизма от любого n-го колеса равно 1 минус передаточное отношение от этого же самого колеса к солнечному колесу, при неподвижном водиле.

Дата добавления: 2014-01-20