Графический метод кинематического исследования зубчатых механизмов

Рассмотрим простую зубчатую передачу, состоящую из двух зубчатых колёс внешнего зацепления.

Скорость общей точки Р определим по формуле

,

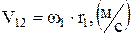где:

.

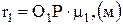Из точки Р к прямой построим отрезок Ра изображающий в масштабе 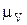скорость точки Р.

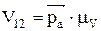
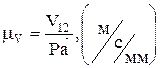
точку а соединим с точкой 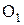, прямой линией. Продолжив эту линию до пересечения с прямой линией перпендикулярной к , получим точку С.

Прямая ас является планом линейных скоростей 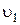(тэтэ-линией) для точек первого колеса, т.е. геометрическим местом концов векторов скоростей точек этого колеса.

Треугольник 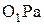- называется треугольником линейных скоростей для колеса 1.

Прямая 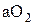, является планом линейных скоростей 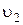для звена 2 (тэтэ-линией)

Определим угловую скорость 1 колеса

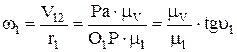
(2.2)

Аналогично из треугольника :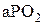

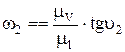
То есть, тангенсы углов наклона тэта-линий треугольников линейных скоростей пропорциональны угловым скоростям соответствующих колёс.

Следовательно, передаточное отношение будет равно:

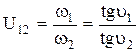
Если тэта-линии, т.е. углы 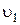, и 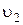откладываются в одну сторону от линий центров (по часовой стрелке или против неё), то передаточное отношение положительное (колёса вращаются в одну сторону).

В противном случае передаточное отношение отрицательное (колёса вращаются в разные стороны).

Построим картину угловых скоростей (рис. 2.18). Перпендикулярно к линии центров проведём прямую линию β-β.

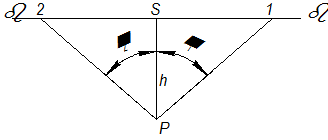
Рис. 2.18

Выберем на этой прямой произвольную точку S, проведём через неё параллель к линии центров и отложим вниз от точки S произвольный отрезок 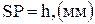. Из точки Р, как из полюса, проведём лучи, параллельные тэта-линиям 1 и 2. Эти лучи пересекут прямую β-β в точках 1 и 2. Рассмотрим треугольник :

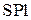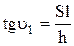
Подставив эту формулу в зависимость (2.40) получим:

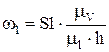
Обозначив

,

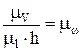получим

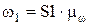
аналогично, 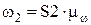,тогда передаточное отношение:

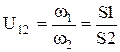
Таким образом, передаточное отношение - это отношение отрезков на картине угловых скоростей (или чисел оборотов в минуту). Допустим, что построенная картина выполнена в масштабе 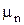, т.е. является картиной чисел оборотов в минуту, так как 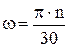, следовательно:

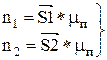
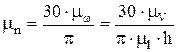
Рассмотрим кинематическое исследование на примере планетарного механизма (рис. 2.19).

Определим скорость 1 колеса:

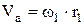
Выбрав масштаб 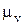, откладываем отрезок 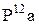. Если соединить точку а с точкой А, то получим тэта-линию колеса 1. Точка 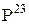третьего колеса неподвижна, т.е. 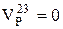. Следовательно, и сателлит 2 в этой точке имеет скорость равную нулю. Таким образом, положение тэта-линии сателлита 2 определяется двумя точками а и 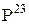. Точка В принадлежит и сателлиту и водилу, поэтому линейную скорость получим, спроектировав точку В на тэта-линию 2. Соединив, точки А и В получим тэта-линии водила Н.

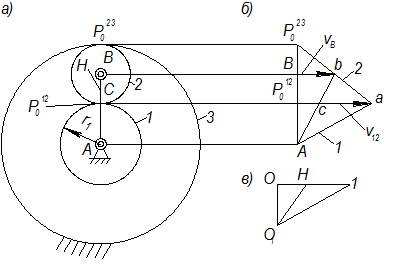
Рис. 2.19

Дата добавления: 2014-01-20